前言
本周通过老师课上对汉诺塔问题的介绍,对递归有了基础认识。为了加深对递归问题的理解,运用python实现汉诺塔问题,使用的编译器为pycharm。
一、什么是汉诺塔问题
现有a、b、c三个柱子,a柱上按从大到小的顺序依次放入n个盘子。需将a柱上的盘子全部挪到c柱上,且挪动过程中大盘子不能放于小盘子之上。
二、实现步骤
1.方法
(1)将a柱上的n-1个盘子(n>1)挪到b柱上;
(2)将a柱上剩下的最后一个盘子挪到c柱上;
(3)将b柱上的n-1个盘子挪到c柱上;
(4)当n=1时,直接将盘子从a柱挪到c柱上。
2.代码实现
def mov(n,a,b,c):
if n == 1:
print(a,'->',c)#当n=1时,直接将盘子从a柱挪到c柱上
else:
mov(n-1,a,c,b) #将a柱上的n-1个盘子(n>1)挪到b柱上
mov(1,a,b,c) #将a柱上剩下的最后一个盘子挪到c柱上
mov(n-1,b,a,c) #将b柱上的n-1个盘子挪到c柱上
num = abs(int(input('a柱上原始有几个盘子:')))
print('\n移动步骤为:')
mov(num,'a','b','c')
3.运行结果
当n=3时:
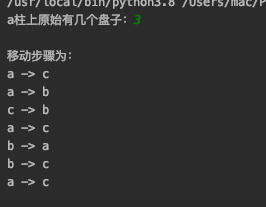
当n=4时:
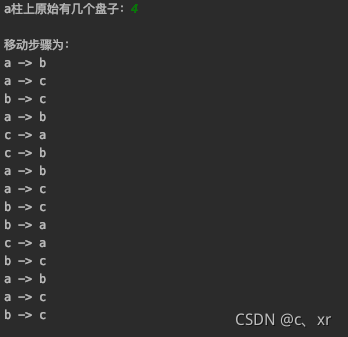
总结
汉诺塔问题是最典型的递归案例,当n=3时,可以将问题分成先移动两个再移动最后一个,当n=4时则是先移动三个再移动最后一个而移动三个的问题又回到了n=3时。以此不停的递归调用函数直到问题被分解成最小规格即触发递归的结束条件,将问题解决。