下面知识点本次考试不设计题目:特殊矩阵存储、广义表、线索树、十字链表、邻接多重链表、最短路径的弗洛伊德算法、关键路径、平衡二叉树、B树、B+树、归并排序、基数排序、外部排序等原理和实现。
一
1. 数据结构的定义、逻辑结构和存储结构。
定义
数据结构是相互之间存在一种或多种特定关系的数据元素的集合
数据结构就是带结构的数据元素的集合
结构就是指数据元素间存在的关系
数据结构的层次
逻辑结构
- 线性结构 一对一
线性表
栈和队列
串和数组 - 非线性结构
树形结构 一对多
图形结构 多对多
储存结构
顺序存储——借助元素在存储器中的相对位置来表示数据元素间的逻辑关系
链式存储——借助指示元素存储的地址的指针表示数据元素间的逻辑关系
2. 时空复杂度分析
尤其是能熟练使用大O函数进行时间复杂度估算。
//O(1)
for(i=0;i<100000;i++)
//O(log 2 n) (以2为底
i=1;
while(i<n)
i=i*2;
//O(n)
for(i=0;i<n;i++)
二.线性表
1. 线性表的顺序存储和链式存储的特点
顺序存储(随机存取):用地址连续的存储单元依次存放线性表中的数据元素(逻辑上和物理上都相邻
链式存储(顺序存取):用一组地址任意的存储单元存放线性表中的数据元素
2. 线性表的基本实现和操作
实现
顺序
typedef struct {
ElemType *elem; //存储空间的基地址,动态分配数组
int length; //当前长度
} SqList;
/*
动态分配数组:
SqList L;
L.elem = new ElemType[MAXSIZE]; //为顺序表分配一个大小为MAXSIZE的数组空间
*/
链式
typedef struct LNode
{
ElemType data; //结点的数据域
struct LNode *next; //结点的指针域
} LNode, *linkList;
//nkList为指向结构体LNode的指针类型
linkList L=xxxx; //创建一个指向节点的指针,通常在对链表进行操作时会先声明
L = new LNode; //生成新结点作为头结点,用头指针L指向头结点
操作
线链表的插入、删除、查找、等算法
Status InitList(linkList &L)//创建有头节点的表
{
L = new LNode;//生成新结点作为头结点,用头指针L指向头结点
L->next=NULL;//头结点的指针域置空
return OK;
}
Status InitList(linkList &L) // 构造一个空表
{
L = NULL;
return OK;
}
Status ListInsert(linkList &L, int i, ElemType e)
{
int j=0;
linkList p=L; //创建指针用来遍历表
while(p&&j<i-1)
{
j++;
p=p->next
}
if(!p||j>i-1)
return 0;
linkList q = new LNode;//生成新结点,q指针指向该结点
q->data=e;
q->next=p->next;
p->next=q;
return 1;
}
Status ListDelete(linkList &L, int i)//删除
{
int j=0;
linkList p=L;
while(p&&j<i-1)
{
j++;
p = p->next;
}
if(!p||j>i-1)
return 0;
linkList q;
q = p->next;
p->next = q->next;
delete q;
return 1;
}
void CreateList_R(LinkList &L)//后插法
{
linkList p=L;
while(p->next)
{
p=p->next;
}
while(!cin >> ch)
{
linkList q = new LNode;
q->data=ch;
p->next=NULL;//!!!!!
p->next = q;
p=q;
}
}
/*
步骤
1.先创建指针用来遍历表
2.进行插入等操作时要先动态分配节点
然后判断是否在连表内可执行
最后才能赋值插入
3.创建节点p后有时(初始化,创建链表)需要p->next=NULL;
*/
三.栈和队列
1. 栈和队列的定义、操作特点
都是限制在表的一端进行插入和删除运算的线性表
- 栈 ( 先进后出):插入删除一端为栈顶,另一端为栈底
- 队列 (先进先出):在队尾插入,在队头删除
2.栈和队列的实现和基本操作
栈的实现和基本操作
定义实现
//顺序栈
typedef struct {
SElemType *base;//栈底指针
SElemType *top;//栈顶指针
int stacksize;//栈可用的最大容量
} SqStack;
//链栈
typedef struct StackNode {
SElemType data;
struct StackNode *next;
} StackNode, *LinkStack;
操作(顺序栈)
因为链栈与线性表相似,所以不再写出
Status InitStack(SqStack &s)//顺序栈的初始化
{
s.base = new SElemType[MAXSIZE];
if(!s.base)
exit(0);
s.top=s.base;
s.stacksize = MAXSIZE;
}
void DestroyStack(SqStack &s)//销毁栈S
{
delete []s.base;
s.base=s.top=NULL;
s.stacksize = 0;
}
Status Push(SqStack &s, SElemType e)// 顺序栈的入栈
{
if(s.top-s.base==s.stacksize)
return 0;
else
{
*(s.top++)=e;
return OK;
}
}
SElemType GetTop(SqStack s)
{
if(s.base==s.top)
return 0;
else
{
return *(s.top-1);
}
}
/*
判断是否栈空或栈满
*/
队列的实现和基本操作
定义实现
在这里插入代码片
typedef struct QNode {
QElemType data;
struct QNode *next;
} QNode, *QueuePtr;
typedef struct {
QueuePtr front; //队头指针
QueuePtr rear; //队尾指针
} LinkQueue;
操作
/***链队的基本操作***/
#include<iostream>
#include<cstdlib>
#include<cstdio>
using namespace std;
#define MAXQSIZE 6
#define OK 1
#define ERROR 0
#define OVERFLOW -2
typedef int QElemType;
typedef int Status;
//- - - - - 队列的链式存储结构- - - - -
typedef struct QNode {
QElemType data;
struct QNode *next;
} QNode, *QueuePtr;
typedef struct {
QueuePtr front; //队头指针
QueuePtr rear; //队尾指针
} LinkQueue;
//算法3.16 链队的初始化
Status InitQueue(LinkQueue &q) //构造一个空队列Q
{
q.front = q.rear = new QNode; //生成新结点作为头结点,队头和队尾指针指向此结点
q.front->next = NULL; //头结点的指针域置空
return OK;
}
void DestroyQueue(LinkQueue &q)
{
/* 销毁队列Q(无论空否均可) */
for(QueuePtr p = q.front, q; p; ) {
q = p->next;
delete p;
p = q;
}
}
Status QueueEmpty(LinkQueue q)
{
/****在此下面完成代码************/
return q.rear==q.front;
/***********************************/
}
int QueueLength(LinkQueue q)
{
/****在此下面完成代码************/
int len=0;
QueuePtr p = q.front->next;
while(p)
{
p=p->next;
len++;
}
return len;
/***********************************/
}
//算法3.17 链队的入队
Status EnQueue(LinkQueue &q, QElemType e) //插入元素e为Q的新的队尾元素
{
/****在此下面完成代码************/
QueuePtr p = new QNode;
p->data=e;
//
p->next=NULL;
q.rear->next=p;
q.rear=p;
return OK;
/***********************************/
}
//算法3.18 链队的出队
Status DeQueue(LinkQueue &q, QElemType &e) //删除Q的队头元素,用e返回其值
{
/****在此下面完成代码************/
if(q.rear==q.front)
return ERROR;
QueuePtr z;
z=q.front->next;
e=z->data;
q.front->next=z->next;
delete z;
return OK;
/***********************************/
}
//算法3.19 取链队的队头元素
QElemType GetHead(LinkQueue q) //返回Q的队头元素,不修改队头指针
{
/****在此下面完成代码************/
return q.front->next->data;
/***********************************/
}
void PrintQueue(LinkQueue q)
{
QueuePtr p;
for(p = q.front->next; p; p = p->next) {
cout << p->data;
if(p->next != NULL)
cout << ' ';
}
cout << endl;
}
循环队列
队满条件:
(q.rear+1)%MAXQSIZE==q.front
队列长度:
q.rear-q.front+MAXQSIZE)%MAXQSIZE
/***循环队列基本操作***/
#include<iostream>
#include<cstdlib>
#include<cstdio>
using namespace std;
#define MAXQSIZE 6
#define OK 1
#define ERROR 0
#define OVERFLOW -2
typedef int QElemType;
typedef int Status;
typedef struct {
QElemType *base;//初始化时动态分配存储空间
int front;//头指针
int rear;//尾指针
} SqQueue;
//算法3.11 循环队列的初始化
Status InitQueue(SqQueue &q) //构造一个空队列Q
{
q.base = new QElemType[MAXQSIZE]; //为队列分配一个最大容量为MAXSIZE的数组空间
if(!q.base)
exit(OVERFLOW); //存储分配失败
q.front = q.rear = 0; //头指针和尾指针置为零,队列为空
return OK;
}
void DestroyQueue(SqQueue &q)
{
/* 销毁队列Q,Q不再存在 */
if(q.base)
delete []q.base;
q.base = NULL;
q.front = q.rear = 0;
}
//算法3.12 求循环队列的长度
int QueueLength(SqQueue q) //返回Q的元素个数,即队列的长度
{
/****在此下面完成代码***************/
return ((q.rear-q.front+MAXQSIZE)%MAXQSIZE);
/***********************************/
}
bool QueueEmpty(SqQueue q)
{
/****在此下面完成代码***************/
return (q.front==q.rear);
/***********************************/
}
//算法3.13 循环队列的入队
Status EnQueue(SqQueue &q, QElemType e) //插入元素e为Q的新的队尾元素
{
/****在此下面完成代码***************/
{
if((q.rear+1)%MAXQSIZE==q.front)
return ERROR;
q.base[q.rear]=e;
q.rear=(q.rear+1)%MAXQSIZE;
return OK;
}
/***********************************/
}
//算法3.14 循环队列的出队
Status DeQueue(SqQueue &q, QElemType &e) //删除Q的队头元素,用e返回其值
{
/****在此下面完成代码***************/
if(q.front==q.rear)
return ERROR;
e=q.base[q.front];
q.front=((q.front+1)%MAXQSIZE);
return OK;
/***********************************/
}
//算法3.15 取循环队列的队头元素
QElemType GetHead(SqQueue q) //返回Q的队头元素,不修改队头指针
{
/****在此下面完成代码***************/
return q.base[q.front];
/***********************************/
}
void PrintQueue(SqQueue q)
{
for(int i = q.front; i != q.rear; i = (i + 1) % MAXQSIZE) {
if(i != q.front)
cout << ' ';
cout << q.base[i];
}
cout << endl;
}
四.串
串的概念
串:由零个或多个任意字符组成的有限序列
子串:任意个连续字符组成的子序列,包含字串的串对应称为主串
空串:零个字符的串(与空格串不同
定义实现
顺序存储
typedef struct{
char ch[MAXLEN+1];
int length;
}SString;
链式存储
typedef struct{
char ch[CHUNKSIZE];
struct Chunk *next;
}Chunk;
typedef struct{
Chunk *head *tail;
int curlen
}HString;
!?!串模式匹配算法思想与实现
BF算法
依次比较,最坏为O(m*n)
/*
匹配失败则回溯
主串: i=i-j+1+1
魔术串:j=1
*/
int Index_BF(SString S,SString T,int pos)
{
int i=pos,j=1;
while(i<=S.length&&j<=T.length)
{
if(S.ch[i]==T.ch[j]
{
i++;
j++;
}
else
{
i=i-j+1;
j=1;
}
if(j>=T.length)
return i-T.length;
else
return 0;
}
}
KMP算法
提速到O(m+n)
nextval更快
void get_nextval(SString T,int &next[])
{
i=1;
next[1]=0;
j=0;
while(i<T.length)
{
if(j==0||T.ch[i]==T.ch[j])
{
i++;
j++;
if(T.ch[i]!=T.ch[j])
nextval[i]=j;
}
else
nextval[i]=nextval[j];
}
}
void get_next(SString T,int &next[])
{
i=1;
next[1]=0;
j=0;
while(i<T.length)
{
if(j==0||T.ch[i]==T.ch[j])
{
i++;
j++;
next[i]=j;
}
else
j=next[j];
}
}
/*
匹配失败则回溯
主串: i不变
魔术串:j=next[j]
*/
int Index_BF(SString S,SString T,int pos)
{
int i=pos,j=1;
while(i<=S.length&&j<=T.length)
{
if(S.ch[i]==T.ch[j]
{
i++;
j++;
}
else
{
j=next[j];
}
if(j>=T.length)
return i-T.length;
else
return 0;
五.二叉树
1. 二叉树的定义、性质
定义:
-
二叉树是n个节点所构成的集合,他或为空树,(n=0)或为非空树。对于非空树:
- 有且仅有一个根节点
- 除根结点外其余节点为两个互不相交的子集T1和T2,分别为左子树和右子树(不能交换顺序)且T1T2本身都是二叉树
-
二叉树节点的度不超过2。子树有左右之分,次序不能颠倒。有五种基本形态。
性质:
- 第i层至多有2^(i-1)个节点
- 深度为k的二叉树至多有2^k-1个节点
- 叶子节点(度为0)=其他节点(度都为2)+1
- n个节点的完全二叉树的深度为[log2n]+1(向下取整如7.1为7)
- 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从1开始编号
概念不好理解,但是看图就很容易理解- 若i=1,则该节点为根,否则编号i/2的节点为其双亲节点
- 若2i>n,则该节点无左孩子,否则编号为2i的节点为其左孩子节点
- 若2i+1>n,则该节点无左孩子,否则编号为2i+1的节点为其左孩子节点
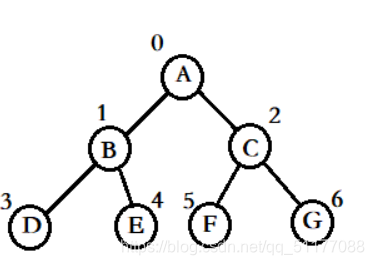
2. 对任何一棵二叉树能够写出它的先序、中序和后序序列
先序:根,左,右
中序:左,根,右
后续:左,右,根
3. 遍历二叉树的定义、方法(先序、中序和后序
定义实现
typedef string Element
typedef struct BiNode
{
Element data;
struct BiNode *lchild *rchild
}BiNode,*BiTree
操作
创建
void Creat(BiTree &T)
{
char ch[20];
if(!cin >> ch)
exit(0);
if(ch[0]=='#')
T=NULL;
else
{
T = new BiNode;
T->data=ch;
Creat(T->lchild);
Creat(T->rchild);
}
}
遍历
先序
void Order(BiTree T)
{
cout << T->data ;
Order(T->lchild);
Order(T->rchild);
}
层次遍历
原理:利用队列存放
void FoundTree(BiTree &t)
{
if(t==NULL)
return;
queue <BiTree> fk;
BiTNode *flag;
fk.push(t);
while(!fk.empty())
{
flag=fk.front();
fk.pop();
printf(" %c",flag->data);
if(flag->lchild)
fk.push(flag->lchild);
if(flag->rchild)
fk.push(flag->rchild);
}
}
4. 掌握二叉树求叶子节点、高度、总节点数、左右子树交换等算法。
叶子节点
int LeafNodeCount(BiTree T)
{
if(T==NULL)
return 0;
else if(T->lchild==NULL&&T->rchild==NULL)
return 1;
else
return LeafNodeCount(T->lchild)+LeafNodeCount(rchild);
}
高度
int Depth(BiTree T)
{
int m,n
if(T==NULL)
return 0;
else
m=Depth(T->lchild);
n=Depth(T->rchild);
if(m>n)
return m+1;
else
return n+1;
}
总结点数
int NodeCount(BiTree T)
{
if(T==NULL)
return 0;
else
return NodeCount(T->lchild)+NodeCount(rchild)+1;
}
左右子树交换
void SwapTree(BiTree &T)
{
BiTree S;
if(T==NULL)
return;
else
{
S=T->lchild;
T->lchild=T->rchild;
T->rchild=s;
}
SwapTree(T->lchild);
SwapTree(T->rchild);
}
}
六.哈夫曼树
掌握哈夫曼树的构造方法
会设计哈夫曼编码及带权路径长度的计算。
七.图
掌握图的基本概念
定义
图Graph=(V,E)
- V:顶点的有穷集合
- E:边的有穷集合