目录
leetcode 451 根据字符出现频率排序 计数排序的应用
1 基础概念
排序问题,就是将无序序列排成一个有序序列(升序或降序)。
2 插入排序
基本思想
即边插入边排序,每步将一个待排序的对象,按其关键码大小,插入到前边已经排好序的一组对象的适当位置上,直到全部对象全部插入为止,插入过程中始终保持当前子序列有序。

虽说是边插入边排序,貌似一边输入一遍插入排序,像打牌一样,但通常情况下我们都是拿到一个待排序的无序序列,然后进行排序后输出有序序列。即真实过程并不是我们一遍输入一遍排序,而是给定一个无需序列a:
在插入a[i]前,数组a的前半段(a[0]~a[i-1])是有序段,后半段(a[i]~a[n-1])是停留在输入次序的无序段。
插入a[i]使a[0]~a[i]有序,就是要为a[i]找到一个插入位置j(0<=j<=i),将a[i]插入到a[j]的位置上之后,有序子序列长度加1.
可见插入排序的关键在于确定插入位置的方法,基于插入方法的不同,插入排序可分为三种:直接插入排序、二分插入排序、希尔排序。
直接插入排序
直接插入排序概述
主要思想是用顺序查找法查找到插入位置然后插入。
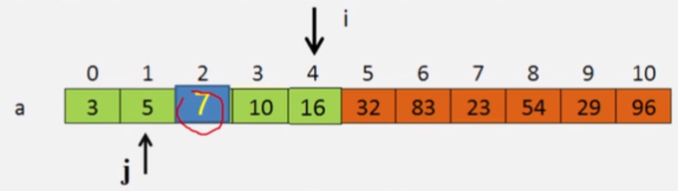
比如上图中一个待排序的数列,i前边的部分是已经排好序的部分,i后边的部分是未排序的。当需要把i插入到前边完成排序时,先复制i的值,然后从 j = i - 1的位置往前找,如果j位置上元素大于i位置上元素,就将j位置上元素后移,然后j前移。这也是为什么我们要先复制i位置的值的原因,因为前边元素后移会覆盖后边元素。
因此主要代码逻辑为:
x = a[i]; // 复制待排序的值
for(j = i - 1; j >= 0 && x < a[j]; --j){
a[j - 1] = a[j]; // 如果j位置上值大于i位置,且j大于0,那么继续往前查找
}
a[j + 1] = x; // 如果当前j位置的值小于i位置,那么就把i位置上的值插入到j+1的位置,注意j+1位置上的值在上一次的时候刚刚后移,因此直接用x覆盖j+1位置上的值即可以上代码在每次循环中都要进行两次比较,一次是待插入元素与当前遍历元素的比较,一次是判断j是否是有效索引的比较,类似顺序查找中的做法,我们可以设置一个哨兵,来减少一次比较。使用哨兵之后,就不用判断索引j的有效性了。具体做法如下,即每次都将待插入的元素复制到数组开头作为哨兵。
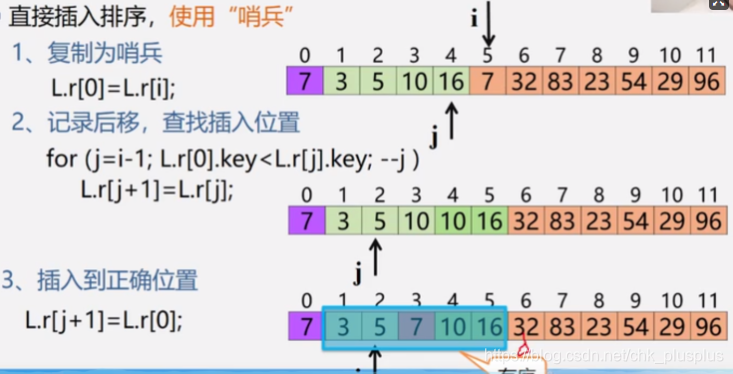
void InsertSort(SqList &L){
int i, j;
for(i = 2; i <= L.length; ++i){
if(L.r[i].key < L.r[i - 1].key){ // 如果待插入元素比它前一个位置元素大,那就放原地就行
L.r[0] = L.r[i]; // 把待插入元素复制到0号位置做哨兵
for(j = i - 1; L.r[0].key < L.r[j].key; --j){
L.r[j + 1] = L.r[j]; // 如果哨兵小于j位置元素,那么将j位置元素后移
}
L.r[j + 1] = L.r[0]; // 把哨兵插入到j位置的后一个位置
}
}
}直接插入排序复杂度分析
实现排序的基本操作有两个,一个是比较序列中两个关键字的大小,一个是移动序列中的记录。
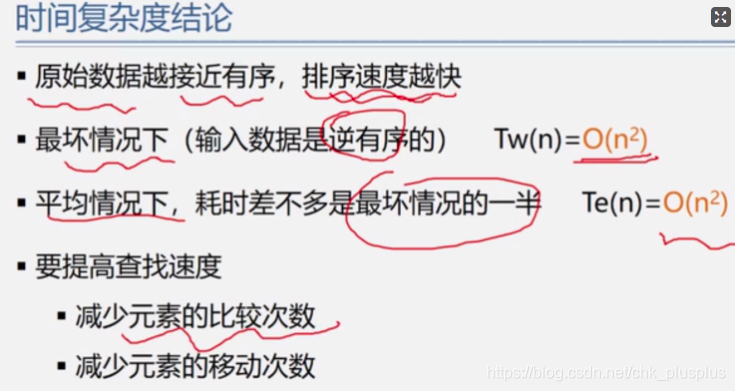
最好的情况:原始序列中关键字顺序有序

最坏的情况:原始序列中关键字逆序有序

平均的情况:
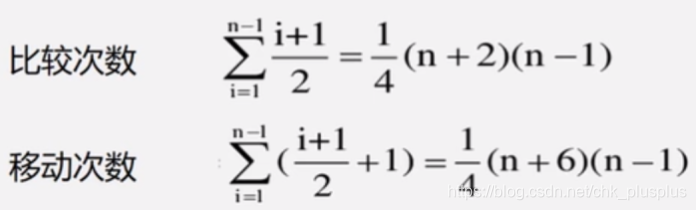
最坏情况下和平均情况下时间复杂度都是平凡阶,最优情况当然是线性阶。
空间复杂度常数阶。
是一种稳定的排序方法。
二分插入排序
主要思想
直接插入排序中用顺序查找来找到插入位置,二分插入排序则使用二分查找来确定插入位置。
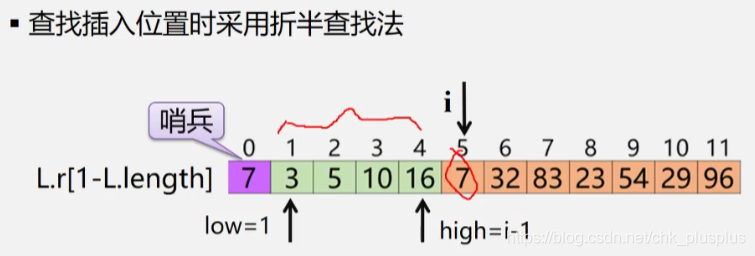
因为i位置之前是已经拍好序的,因此可以用二分查找。
void BInsertSort(SqList &L){
for(int i = 2; i <= L.length; ++i){
L.r[0] = L.r[i]; // 当前元素复制到0号位置做哨兵,其实并没有起到哨兵的作用,只是复制了一份
int low = 1, high = i - 1; // 确定二分查找初始区间
while(low <= high){
mid = (low + high) / 2;
if(L.r[0].key < L.r[mid].key){ // 插入位置在前半区间
high = mid - 1;
}else low = mid + 1;
} // 循环阶数,high + 1为插入位置
for(int j = i - 1; j >= high + 1; --j) L.r[j + 1] = L.r[j]; // 移动元素
L.r[high + 1] = L.r[0]; // 将哨兵插入到正确位置
}
}二分插入排序效率分析
首先,由于二分查找比顺序查找效率高,所以二分插入排序平均性能肯定是超过直接插入排序的。
具体还是要看比较次数与移动次数。
比较次数:
二分查找的比较次数值与对象个数有关,与数列原始排列无关。
当n较大时,总的比较次数比直接插入排序最坏情况好的多,但是比其最好情况要差。
当初始排列已经有序或接近有序时,直接插入排序比二分插入排序比较次数好(其实就是直接插入的最好情况要比二分插入排序好)。
移动次数:
二分插入排序移动次数与直接插入排序一样,依赖于初始排列。
即二分插入排序优化了比较次数,但是没有优化移动次数。

希尔排序
基本思想
在直接插入排序中,我们每次插入一个元素,都要把前边有序部分依次遍历一遍。并且我们知道,当原序列基本有序时,直接插入排序效率会很高。因此提出了希尔排序来从这两方面改进直接插入排序:
? ? ? ? 先将整个待排记录序列分割成若干子序列(子序列中元素对应到原序列中元素不连续),分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行一个直接插入排序。
也就是说希尔排序实际上是进行了多遍插入排序,且刚开始时候的插入排序对应的元素在元素列中间隔更大,因此可以依次把元素移动更多步数。
看下边例子:
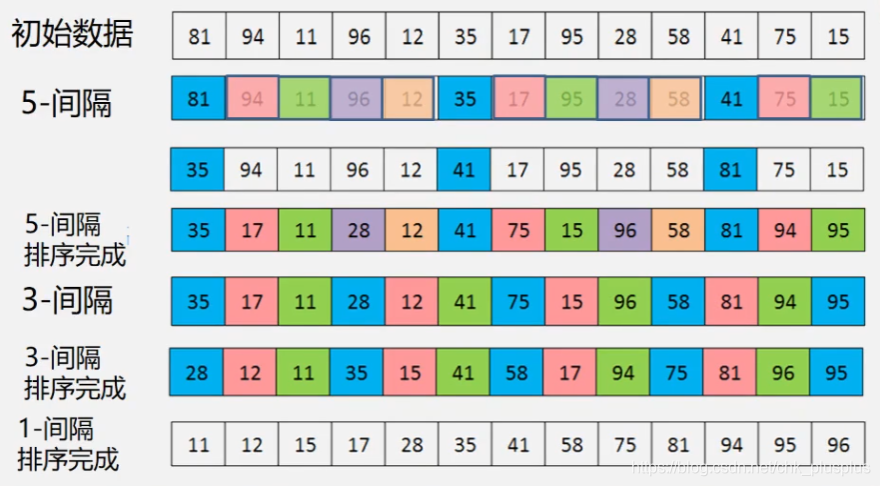
第一次子序列插入排序:如图中5-间隔那一行中3个蓝色方块81,35,41,它们就是本次直接插入排序的序列,是在原序列中每五个元素抽一个形成的一个子序列。直接插入排序完成后就形成了35,41,81的排序。然后再从94开始,每5个元素抽一个组成子序列92,17,75,继续进行直接插入排序,接下俩还有11,95,15,等子序列待排序。本次插入排序可以一次让元素移动5步,而不是一步一步移动的。
第二次子序列插入排序:从图中5间隔排好序的首元素35开始,每3个元素抽一个元素组成子序列,仍进行直接插入排序。然后从17开始,每3个元素抽取子序列,直接插入排序。一直到序列中所有元素都完成了3间隔的直接插入排序。
最后一次子序列插入排序:最后一个1间隔直接插入排序,其实就是直接对整个序列进行直接插入排序,但是由于上边5间隔和3间隔排序的完成,此时序列已经基本有序了,因此最后进行直接插入排序时候的效率会很高。
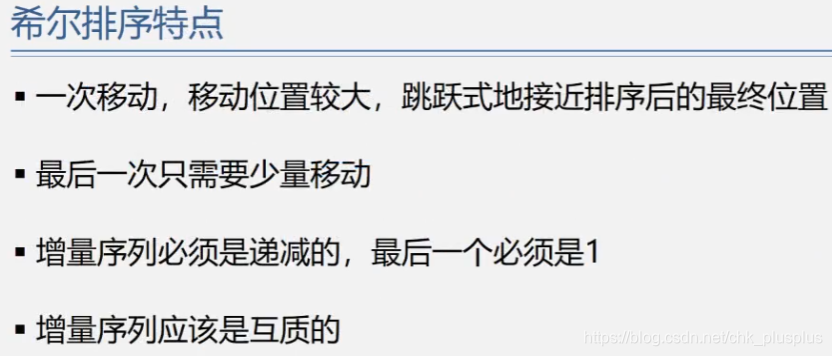
希尔排序的特点有两个:
? ? ? ? 缩小增量;
? ? ? ? 多遍插入排序;
多遍插入排序就不说了,缩小增量的意思是,多轮插入排序中的增量序列是递减的,且增量序列是互质的,最后一个必须是1。
希尔排序复杂度分析
希尔排序算法效率与增量序列的取值有关,但是小于最坏情况还是小于直接插入排序的平方阶的。但希尔排序是一种不稳定的排序算法。希尔排序不适合在链式存储结构上实现。

总结:

3 交换排序
基本思想
基于插入的方法主要操作是比较和移动,待插入元素与当前元素比较,如果当前元素大于待插入元素,则将当前元素后移。而基于交换的排序主要思想是将序列中两个元素进行比较,如果他们之间的大小顺序与我们要排的顺序是相反的,则将他们交换。即基于交换的排序方法主要操作是比较和交换。
冒泡排序
冒泡思想
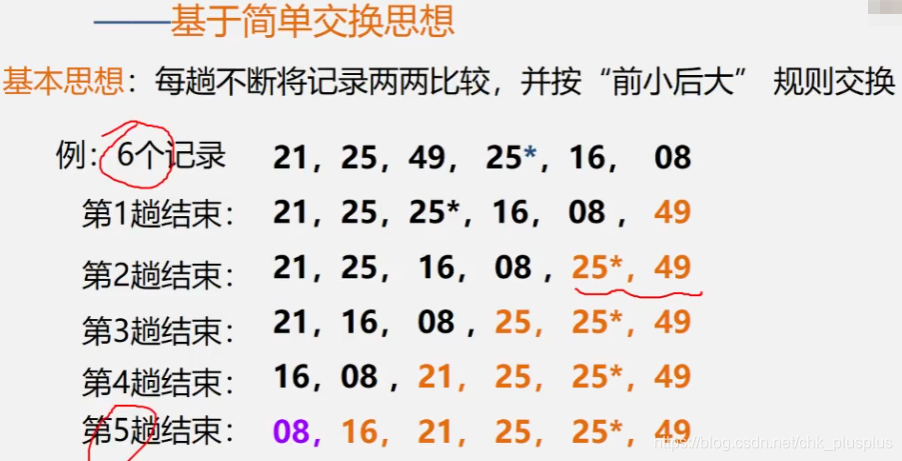
每趟比较相邻位置的两个元素,然后按规则交换,对于一个含有m个元素的序列,只需要5趟比较就可以完成排序。如下图,第一趟结束,我们已经将整个序列中最大值放在了最后边,第二趟的时候不用再比较最后一个值,因为那个一定是最大的,因此只需要比较前m-1个值就行了,等到低5趟的时候,只需要比较前两个值的相对大小就行了。
冒泡特点
每趟结束时,都能挤出一个最大值到最后边位置,同时还能部分理顺其它元素。
但是有时候对于m个记录的序列,我们不需要m-1趟交换。
如果在某一趟的时候我们发现没有发生记录交换,那么说明整个序列已经排好序了,后边的趟就不用进行了,直接结束算法。
冒泡效率分析
最好情况:
序列本来就是有序的,这样一趟下来发现一次交换操作也没做,直接结束算法。

最坏情况:
序列逆序,第一趟比较n-1次,第二趟比较n-2次,第三趟比较n-3次,,,最后一趟比较1次,等差数列求和。
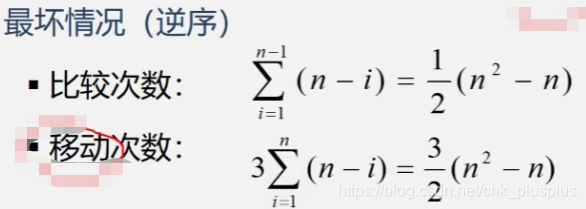

快速排序
基本思想
枢轴一般选择第一个数就行。

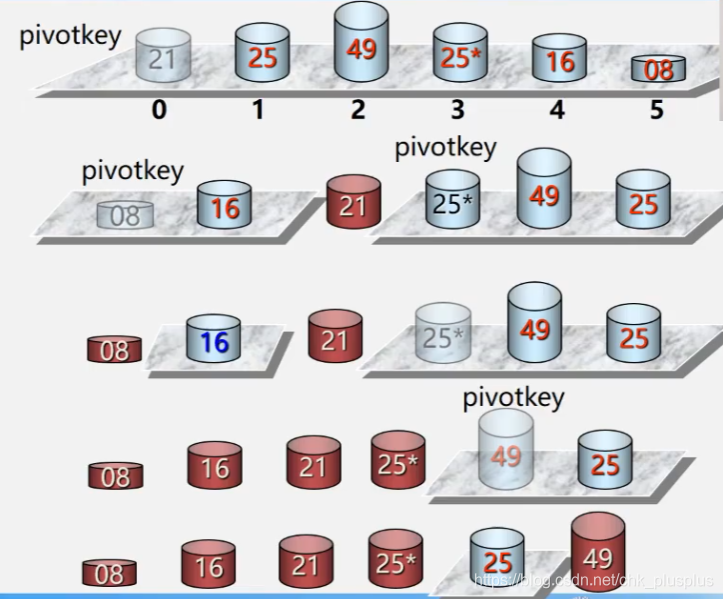
快排复杂度



快速排序的时候原始序列越乱越好,越有序则性能越差

C++冒泡&快排实现
通常用两个函数实现,一个用来递归实现整个序列的排序,一个用来进行快排中的一轮排序。一轮排序指的是在一个子表中选取一个枢轴,然后将比其小的数放在左边,比起大的数放在右边,具体可以参考数据结构与算法基础(青岛大学-王卓)_哔哩哔哩_bilibili
#include <bits/stdc++.h>
using namespace std;
int partition(vector<int> &v, int low, int high){
int pivot = v[low]; // 选表中第一个元素为枢轴
while(low < high){
while(low < high && v[high] >= pivot) --high; // 从后边遍历,如果比枢轴大就不用动(直接遍历前一个),如果比枢轴小就放到前边去
v[low] = v[high]; // low始终代表前边插入位置,high始终代表后边插入位置
while(low < high && v[low] <= pivot) ++low; // 从前边遍历,如果比枢轴小就不用动(直接遍历后一个),如果比枢轴大就放到后边去
v[high] = v[low];
}
v[low] = pivot; // 当low == high的时候,就把枢轴放到这个位置上
return low; //枢轴位置
}
void quick_sort(vector<int> &v, int low, int high){ // 递归排序
if(low < high){ // 递归出口
int pivot_location = partition(v, low, high); // 一轮排序
quick_sort(v, low, pivot_location - 1); // 对左边子表递归排序
quick_sort(v, pivot_location + 1, high); // 对右边子表递归排序
}
}
void bubble_sort(vector<int> &v){
int flag = 1;
int len = v.size();
int temp;
for(int i = 0; i < len - 1 && flag == 1; ++i){ // 注意这里i是从0到len-2一共len-1次,因为长度为len的序列冒泡需要len-1次
flag = 0;
for(int j = 0; j < len -i; ++j){ // 第i趟冒泡,需要比较 len - i - 1次
if(v[j] > v[j + 1]){
flag = 1;
temp = v[j];
v[j] = v[j + 1];
v[j + 1] = temp;
}
}
}
}
int main(){
vector<int> v{23, 5, 65, -3, 33, 789, -654};
int len = v.size();
for(int i = 0; i < len; ++i){
cout<<v[i]<<" ";
}
cout<<endl;
// quick_sort(v, 0, len - 1);
bubble_sort(v);
for(int i = 0; i < len; ++i){
cout<<v[i]<<" ";
}
cout<<endl;
return 0;
}4 选择排序
简单选择排序
基本操作
就是每次找到当前最小的,然后交换位置。

简单选择排序复杂度分析

堆排序
堆的定义

这里虽然堆的实际是一个完全二叉树,但是不要把堆理解的窄了,只要满足一个序列满足上边的条件那么这个序列就是一个堆,所以堆的本质可以说就是一个满足特定条件的序列,只是可以对应到一个完全二叉树上来帮助理解。所以在堆排序中实际操作的数据结构还是数组,而不是树。
堆排序基本操作

要使用堆排序,主要要解决两个问题,
1. 如何由一个无序序列建成一个堆
2. 如果在输出堆顶元素后,调整剩余元素为一个新的堆
其中第二个问题解决了,第一个问题就解决了,可以通过不断调整,将无序序列建成一个堆,也就是下边讲的,对于一个无序序列反复筛选,就能得到一个堆。
第二个问题即堆的调整:
小根堆调整步骤:
(1)输出堆顶元素之后,以堆中最后一个元素替代它,堆中最后一个元素即数组中最后一个元素,要时刻记得堆排序在实际编码中用的数据结构是数组,而不是树。
(2)将根结点值(注意这是上一步替代过的新值)与左、右子树的根节点值进行比较,并与其中较小者进行交换,左右子树根节点值即存储在数组索引?2i 和 2i + 1 位置上的元素。
(3)重复上述操作,直到叶子结点,将得到新的堆,这个从堆顶到叶子的调整过程叫做“筛选”。
大根堆的调整同理。
堆的建立
首先明确一点,一个堆对应了一个完全二叉树,而完全二叉树中最后一个非叶子结点编号一定是n整除2,即我们在建堆的筛选操作的时候只需要从数组中索引为 n/2的结点开始筛选即可,需要注意的是建堆过程的筛选是自底向上的,即从最后一个非叶子结点进行筛选,一直筛选到根节点,这样才能保证整棵树是堆。在使用堆的时候,输出堆顶元素之后,把最后一个元素移动到堆顶之后,其实这时候只有以堆顶元素为根的树不是堆,因此需要对堆顶元素进行筛选,而以其它非叶子结点为根的树此时仍然是堆,因此只需要对堆顶元素的一次筛选过程就够了。

堆排序算法性能分析
初始化堆时间复杂度是O(N),输出堆顶后调整堆的时间复杂度是O(logN),如果要实现堆排序,则要不断地输出堆顶,把N个元素都输出出去,每输出一次堆顶就需要一次调整(除了最后一次输出堆顶,这个时候就剩一个元素,不用调整),因此整个堆排序的时间复杂度是O(NlogN)


堆排序实例
leetcode 215数组中第K大元素
215. 数组中的第K个最大元素 - 力扣(LeetCode) (leetcode-cn.com)

下面是大顶堆解法,因为是第k大,需要调整输出k-1个元素,并调整k-1次,每次调整的时间复杂度可认为是logN,因此时总的时间复杂度是KlogN
class Solution {
// 大顶堆解法
public:
// i为数组nums中待调整的结点,n是数组中元素个数
void adjust(vector<int> &nums, int i, int n){
int j = 2 * i + 1; // j是i的左叶子结点,加1是因为数组是从0开始索引的
while(j < n){ // 不能超过涉及的元素总数,之所以用 j < n 而不是 j + 1 < n是因为堆对应完全二叉树,有些结点只有左孩子
// 没有右孩子,如果用 j + 1 < n会把只有左孩子且左孩子大于根节点的情况给忽略
if(j + 1 < n && nums[j + 1] > nums[j]) ++j; // 如果右孩子更大,就让j指向右孩子,左孩子更大则j指向左孩子,这里
// 还用 j + 1 < n来解决了只有左孩子的情况,这个时候不用比较左右孩子,直接让左孩子跟根节点比较即可
if(nums[j] < nums[i]) break; // 如果根节点大于其左右孩子,直接返回,不用调整了
else{
swap(nums[i], nums[j]); // 将根节点与比它大的孩子交换
i = j; // 交换之后下一步调整的是原先位置j的结点
j = 2 * i + 1;
}
}
}
void heap_sort(vector<int> &nums){
int n = nums.size(); // n是要调整的数组中元素个数
for(int i = n / 2 - 1; i >= 0; --i){ // n/2-1是第一个非叶子结点,减一的原因是数组从0开始索引
adjust(nums, i, n);
}
}
int findKthLargest(vector<int>& nums, int k) {
heap_sort(nums); // 建堆
int n = nums.size();
for(int i = 0; i < k - 1; ++i){ // 需要注意这里有个坑,第k大,这个k是从1开始的,而i是从0开始的,
// 比如第1大在代码中实上是第0大,如果要求第1大,直接输出堆顶即可,不需要输出堆顶调整,如果要求第2大
// 则输出一个堆顶元素,然后进行一次调整,输出第k大,需要输出k-1个堆顶元素,调整k-1次,这里i只是用来
// 确定调整次数,调整k-1次,那就应该是i从0到k-2
swap(nums[0], nums[--n]); // 堆顶元素输出,最后一个元素放到堆顶,直接把堆顶放到最后一个位置
adjust(nums, 0, n); // 上一语句输出堆顶之后直接将n自减1,刚好调整的时候不用考虑最后一个元素
}
return nums[0];
}
};此外求第k大的数还可以用小顶堆来解,只需要维护一个大小为k的小顶堆,遍历数组中元素,如果比k大就替换堆顶,然后调整,如果比k小就直接遍历下一个,这样遍历完成之后的堆顶元素就是第k大的元素,时间复杂度NlogK
5 归并排序
把两个或两个以上的有序子序列归并成一个有序序列,最常见的是2路归并排序。
归并排序 详解_k_koris的博客-CSDN博客_归并排序
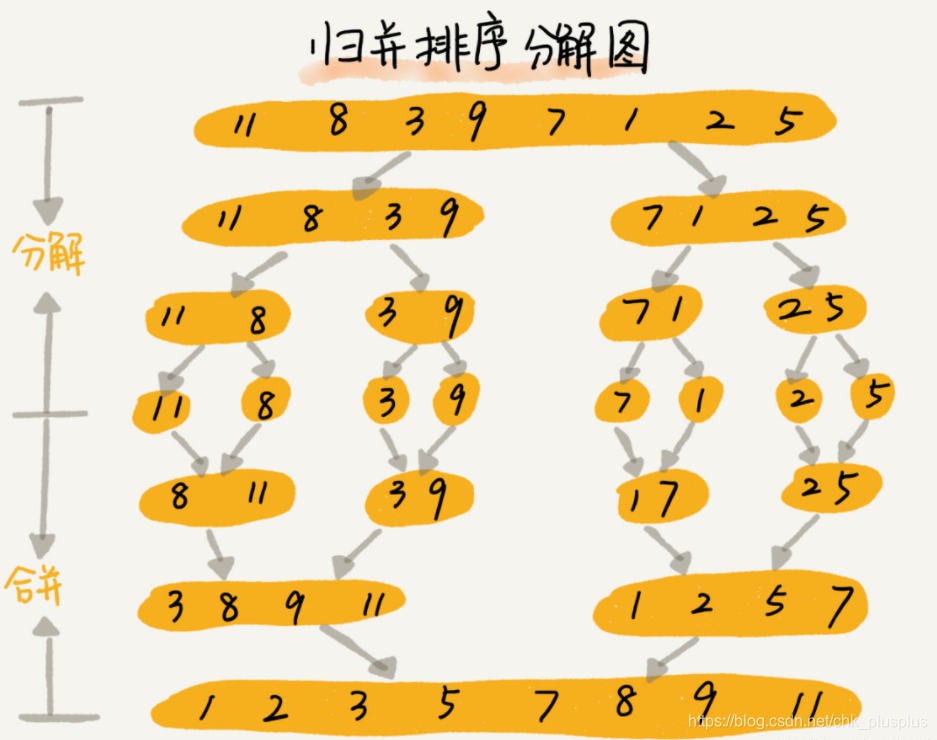
主要是两个函数,一个用来分治,一个用来合并
分治函数一般用递归实现,递归出口是分治区间里只剩下了一个元素。
合并要负责将两个有序序列合并成一个有序序列,合并操作是自底向上的,即从两个区间都只有一个元素开始,直接比较大小合并成一个包含两个元素的有序序列。
#include<bits/stdc++.h>
using namespace std;
// l是左索引,r是右索引,q是中间索引
void Merge(int arr[], int l, int q, int r){
int n = r - l + 1; // 用一个长度为n的临时数组存放合并后的有序序列
int *tmp = new int[n];
int i = 0; // i用来指示临时数组中正要赋值的位置
int left = l; // left用来遍历左边
int right = q + 1; // right用来遍历右边
// 三个while循环,第一个决定让两个数组中对应位置比较小的元素放入tmp临时数组,后边两个意思是如果其中一个已经放完,就将没放完的数组中剩余元素都放入临时数组
while(left <= q && right <= r)
tmp[i++] = arr[left] <= arr[right] ? arr[left++] : arr[right++];
while(left <= q)
tmp[i++] = arr[left++];
while(right <= r)
tmp[i++] = arr[right++];
// for循环把合并之后的有序数组放入原数组
for(int j = 0; j < n; ++j)
arr[l + j] = tmp[j];
delete [] tmp;
}
void MergeSort(int arr[], int l, int r){
if(l == r) return; // 递归出口,区间里只剩下一个元素了,没法分治了
int q = (l + r) / 2;
MergeSort(arr, l, q);
MergeSort(arr, q + 1, r);
Merge(arr, l, q, r); // 先分治,再合并
}
int main(){
int a[5] = {2, 44, -34, 5, 3};
MergeSort(a, 0, 4);
for(int i = 0; i < 5; ++i){
cout<<a[i]<<" ";
}
cout<<endl;
}
最佳/最差/平均时间复杂度:O(N)
空间复杂度:临时数组O(N),递归栈 O(lgN),因此总的空间复杂度O(N)
6 桶排序
非比较排序。
基数排序跟桶排序还是有一点区别,桶排序不是一种具体的排序方法,而是一种思想,基数排序和计数排序都可以算是用了桶排序的思想。基数排序的特点是多关键字。计数排序可参考马士兵说:计数排序,桶思想的一种_哔哩哔哩_bilibili,一般认为与频次有关的是计数排序的应用,比如下边的两道力扣题。
基数排序基本思想
分为分配和收集两个步骤。
分配:设置若干个箱子,将关键字为k的记录放入第k个箱子(注意可能有些箱子直到最后都没放东西,即是空的)。
收集:将非空的箱子连接起来。
一般的排序只能针对一个关键字来排序,而基数排序可以综合多个关键字实现排序。
小例子:

这里的数字是三位数,我们可以认为有三个关键字(个位十位百位),因此需要进行三轮排序,我们按照从个位开始排序的方法,因为三个关键字的取值范围都是0到9,所以三轮排序时候用到的桶的数量都是10
第一轮:
第一趟分配
从数列中第一个数614开始按个位将其放到对应的桶里。
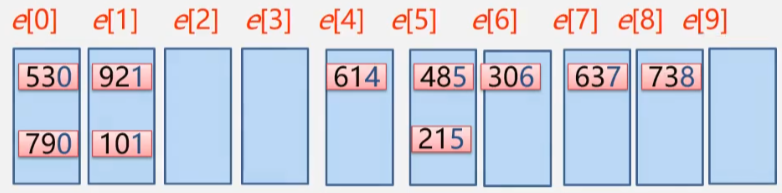
第一趟收集

可以看出经过第一趟分配与第一趟收集,所有的记录在第一个关键字即个位数上已经有序了。
第二轮:
第二轮是在第一轮的基础上进行的。
第二轮分配
从530开始按十位数将不同数字放到对应的桶里。
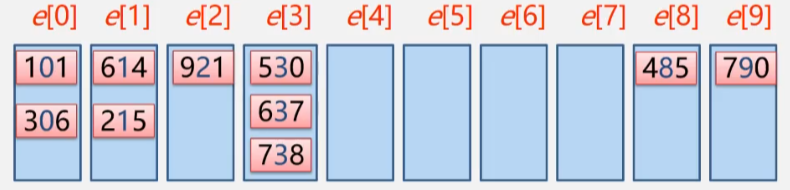
第二轮收集

第三轮:
在前两轮的基础上进行。
第三轮分配
从101开始按百位将数字放到对应的桶里。
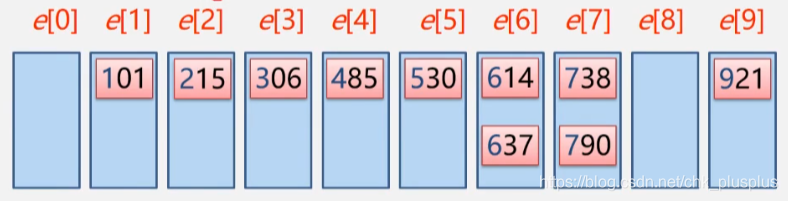
第三轮收集
![]()
第三轮收集之后数列已经有序了,排序完成!
效率分析
时间效率
O(k*(n + m))
n:待排序序列中记录个数,比如上边例子中一共有10个数,n代表分配过程,有n个数我们就要进行n次比较然后将对应的数放到桶里。
m:关键字取值范围,即桶的个数,比如上边例子中因为数字范围0到9,因此有10个桶,收集的时候就要收集10个桶,m代表收集过程。
k:关键字个数,比如上边例子中一共有个位,十位,百位三个关键字,因此k=3,巧的是这三个关键字取值范围都一样,k代表要进行多少轮分配与收集。
空间效率
O(n + m)
n:代表收集过程,要收集回来n个记录。
m:代表桶,需要m个桶。
基数排序是稳定排序。
leetcode 347 前k个高频元素?

时间复杂度是 O(N + K)
可以认为是只有一个关键字情况下的基数排序(对频次这个关键字进行一轮基数排序),也可以认为是计数排序的应用,毕竟跟频次有关。不如以后统称为桶排序吧。
class Solution {
public:
vector<int> topKFrequent(vector<int>& nums, int k) {
int len = nums.size();
unordered_map<int, int> mp;
for(auto num: nums){
mp[num]++; // 哈希表mp的键是数组元素,值是其频率
}
// 虽然桶排序可以排好几个关键字的记录,但是这里我们只用频率这一个关键字做一轮排序,关键字的取值范围即为桶的个数
// 所以要先求出最大频率,即为桶的个数
// 设定桶的个数
int max_fre = 0;
for(auto &m : mp){
if(m.second > max_fre) max_fre = m.second;
}
// 桶排序第一步,分配
vector<vector<int>> bucket(max_fre, vector<int>()); // 一共max_fre个桶,桶的实例是一个int数组,之所以
// 用数组,是因为一个桶中可能分配好几个实例
for(auto j : mp){
if(j.second != 0){ // 如果频率不为0,就按频率将其分配到对应索引的桶中
bucket[j.second - 1].push_back(j.first); // 某元素对应其在桶数组bucket中的索引就是其频率
}
}
// 桶排序第二步,收集
vector<int> ans; // 这里的收集只收集前k个元素即可,因为不是要进行排序,而是找前k个频率的元素,收集当然要用数组
for(int t = max_fre - 1; t >= 0; --t){
if(bucket[t].size()){ // 收集的时候当然不收集空桶
for(auto a : bucket[t]){ // 一个桶中可能有多个元素
ans.push_back(a);
}
}
if(ans.size() == k) return ans; // 收集到k个就撤
}
return {};
}
};leetcode 451 根据字符出现频率排序 计数排序的应用

class Solution {
// 频率排序问题,一般都可以用哈希加桶排序,哈希用于求频率,桶排序用于排序, 频次就是桶索引
public:
string frequencySort(string s) {
// 哈希表求频率
unordered_map<char, int> mp;
for(auto ss : s){
mp[ss]++;
}
// 桶数组初始化
int max_fre = 0;
for(auto m : mp){
if(m.second > max_fre) max_fre = m.second;
}
vector<string> bucket(max_fre, string()); // 因为是用max_fre定义的数组,因此最大索引是max_fre - 1,这里挖了
// 一个坑,频次比索引多1
// 桶排序第一步,分配
for(auto m : mp){
if(m.second) bucket[m.second - 1] += m.first;
}
// 桶排序第二步,收集
string ans;
int j;
for(int i = max_fre - 1; i >= 0; --i){
if(bucket[i].size()){
cout<<bucket[i]<<endl;
for(auto b : bucket[i]){// 一个桶中可能有多个元素
j = i + 1;
while(j--){
ans += b;
}
}
}
}
return ans;
}
};7 内部排序算法总结
内部排序是数据记录在内存中进行排序,外部排序是因为要排序的数据很多,内存不能一次性容纳,因此要访问外存,上边提到的排序算法都是内部排序算法。
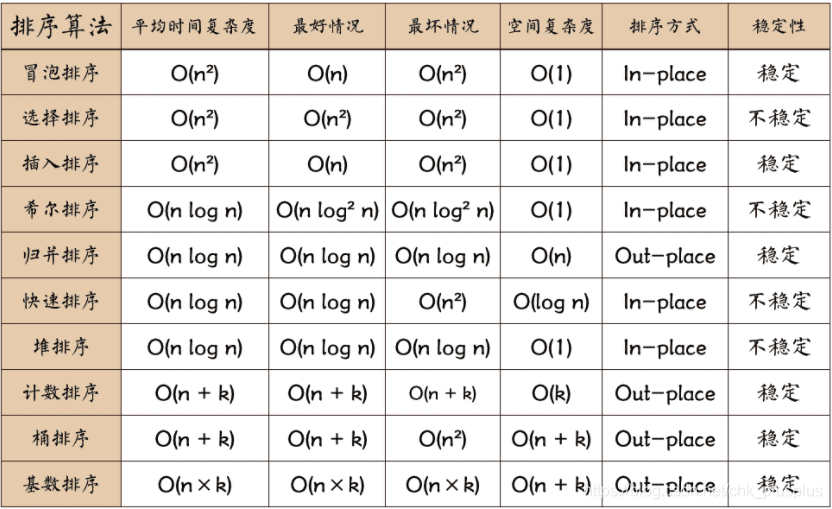
桶排序,基数排序,计数排序是非比较式排序,其它都是基于比较的排序方法。