上周确定了新高考教师评价的数学模型就是使用多层线性模型进行计算,但就在昨天有个数学专家给出了他的否定意见,根据一篇国外的论文 使用多层线性模型关键在第二层组的差异,所以在使用最小测试组时,样本量应满足30/30原则或50/>5的原则,这么说按照学校规模进行计算的话,很有可能对教师增值评价结果不准确,so,只能暂时抛弃

所谓30/30 就是最少30组。每组30人这种规模,即1000人左右,50/>5 即50个组,每组大于5人,算出来的准确性才会最高。对于一个学校来说,1000人的规模没有问题,但对于组的统计就很难划分,尤其是到了高二开始,只有天知道学校是否会有50个班开设历史课或其余的选修课,这样对于教师增值评价这种严肃的事就变成了听天由命,如果在一个系统中存在多种算法考虑到成本那是不可能的,所以还是要回到回归方式对数据进行处理。
接下来的方式就是采用什么样的回归方式解题,这当然要借助spass进行提前估计,找到拟合度最高的方式。经过对N所学校的数据对比,和各科的数据拟合情况,下面是几个样例:
1:
语文成绩:
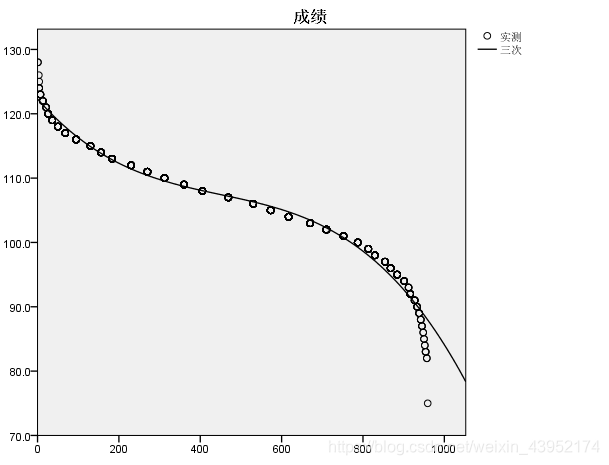
2:数学
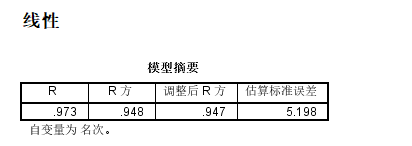
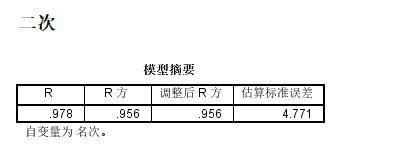

优势三次函数拟合度最高,接下来看看图形是否存在不合理现象
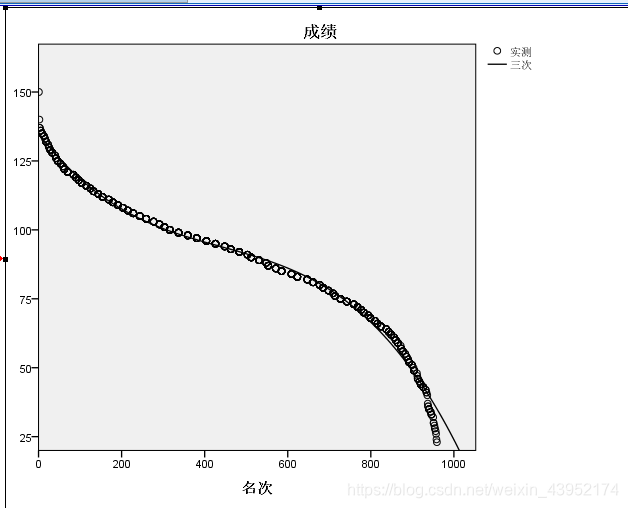
我勒个去,几乎是完美拟合。
3:再看其余选修课
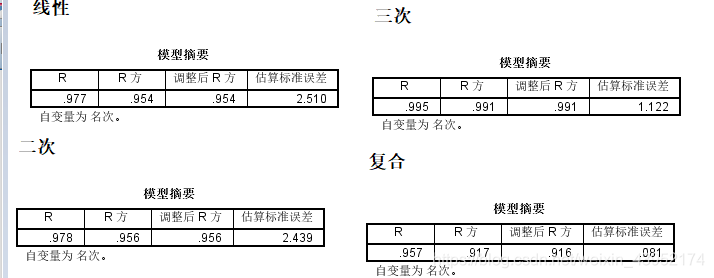
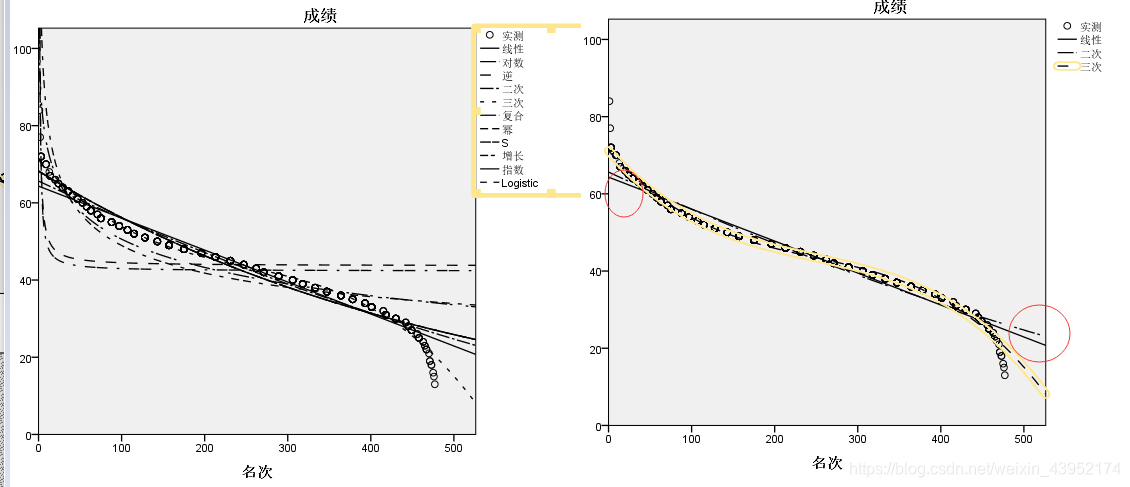
黄色是三次函数,通过对比可以看到,线性回归和二次回归都会造成一定的拟合度偏差,其实,我们还是研究了很多的方式。另外还有一种方式,就是将两次的名次差做Y, 最后一次的名次为X。同样对各种归回做了验证,首先排除了线性回归对教师增值评价的作用,这种算法对好学生和落后生的的计算偏差太大,形成的对教师评价的数据也是不公正客观的,好处是 在写算法的时候相对容易些。
新高考教师增值评价必须是一个非常严谨的事,毕竟这涉及到教师的辛勤付出,同时也能更好的发挥指挥棒的作用,帮助学校改进教学方式,提供过程性参考建议,所以,三次函数尽管比较麻烦,但还是值的做的。