[数据结构与算法]二分算法，你真的觉得自己会？

什么是二分算法：

二分搜索（英语：binary search），也称折半搜索（英语：half-interval search）、对数搜索（英语：logarithmic search），是一种在有序数组中查找某一特定元素的搜索算法。搜索过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜索过程结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空，则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。

二分的使用规则：

二分算法的题，网上的模板太多了，但是别傻用，你得懂它们到底在干什么才对！

同时使用二分的两个模板。
刷题简单总结下来，根据题意设计check函数，判断要找的分界点是哪一个模板，对应选择不同的模板即可。

二分的算法一定要是数组的连续递增吗？ 当然不是（只要有序即可）

一大部分的题目明显的特征就是单调性质，还有一部分就是二段性。
写题解是为了梳理思路，同时锻炼自己的思维整合能力

代码模板是这样的，具体就是要不同的题，设计不同的check函数即可。

		int left = ;
        int right = ;
        int mid = 0;
        while (left < right){
            mid = ();
            if() {
                
            } else{
                
            } 
        }
        return  left;

难度会依次上升，但是都逃脱不了这些模板

lc二分题目

x的平方根

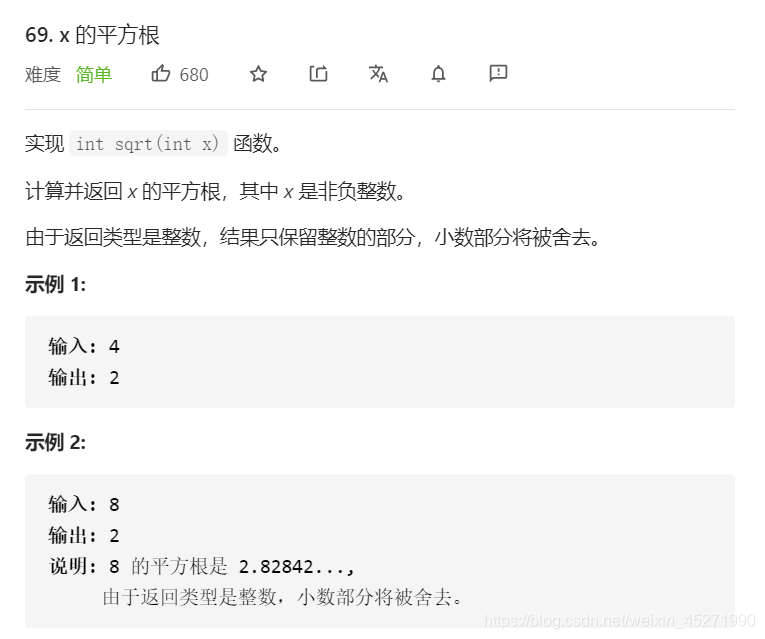
这个题要注意的就是 细节问题

思路一 穷举 然后判断i的平方是不是等于x 但是这样的做法也有不可取的地方就是 不可以被开整数的

思路一，使用已有的java自带函数

class Solution {
    public int mySqrt(int x) {
        return (int) (Math.sqrt(x));
    }
}

思路二： 二分查找
本质上刚开始想到的是使用穷举暴力，然后判断是不是这个数字的平方等于x，二分的本质也就是在穷举上进行了进一步的优化。

class Solution {
    public int mySqrt(int x) {
        //思路三 二分的进行查找 小于等于x 的最后一个来作为check函数
        int left = 0;
        int right = x;
        int mid = 0;
        while(left < right){
            mid =(int)(left+ (long) (right+1) )/2; //这样的加法是否会出现溢出的问题呢？ 需要做处理
            //   mid = (int) (left + (  ( (long)right +1 ) - left)/2  ); 等价的写法二 但是注意数据类型的转换
            //   注意首先需要把right 转换成 long类型 然后进行计算，最后的结果再转换为int
            if(mid <= x / mid) { //同样不写成 mid * mid <= x 也是考虑到数据溢出的问题
                left = mid;
            }else{
                right = mid- 1;
            }

        }
        return left;
    }
}

小tips：
计算mid的两种方式

• (left +right)/2
• left + (right - left)/2 这种做法可以防止数据的溢出

搜索插入位置

这个题主要就是check函数的设计问题。如果数组中存在这个函数，那么需要返回对应的index ，如果不存在，返回插入的位置。因此决定了 必须将check函数设计成 nums[mid] >= target 区间背划分为两端，左边是不满足的，右边是满足的，那么需要找到的分界点就是绿色的点。

/**
 * 这个题尝试使用 不同的check函数来进行二段性的区间的判定
 *
 * 边界出现问题就是
 * 1.数组不指向任何引用 那么 返回-1
 * 2.数组长度为0 那么 返回数组长度
 * 3.数组的最后一个数字都比target小 那么返回数组长度
 *
 * 其他情况 数字存在在数组中 或者是
 *         数字不存在在数组中，但是 最后一个值 是比target的值大的
 *         那么使用二分的模板但只能使用模板一 更新mid也就是找有区间的第一点
 *
 * 关于check函数的问题  nuns[mid] >= target
 * 那么该如何思考这个题呢？ 为什么只能用一 也即是 mid >= target
 * 可以想 如果这个数组存在的话 那么返回这个数字
 * 如果这个数字不存在的话 那么找到的肯定是比这个数字第一个大的位置作为下标插入的位置
 *
 * 如果使用check mid <= target
 * 数字存在 找到的是 相同的
 * 数字不存在 找到的是 比目标值小的第一个 所以不应该使用这个方法
 *
 * 那么根据使用check函数 选择的是右区间里面的第一个 所以使用模板一
 */
public  static int searchInsert(int[] nums, int target) {
        //特例判断
        // 如果数组为空是一种边界  另一种是 如果数数组的最后一个数字都小于target
        // 那么返回数组的长度
        if(nums == null) return -1;
        if(nums .length == 0 || nums[nums.length -1] < target) return nums.length;

        int left = 0;
        int right = nums.length -1;
        while(left < right){
            int mid = (left + right) /2;
            if(nums[mid] >= target){
                right = mid;
            }else{
                left = mid+1;
            }
        }
        return left;
    }

在排序数组中查找元素的第一个和最后一个位置

算法思路：
以nums[mid] >= target 作为check函数 满足条件的右半段的第一个index。 也就是是要寻找元素的左边界。
以nums[mid] <= target 作为check函数 满足条件的左半段的最后一个index。 也就是是要寻找元素的右边界。
可以发现同时使用了右半段（模板一）和左半段（模板二）来做

public static int[] searchRange(int[] nums, int target) {
        //首先判断特例
        if(nums == null) return new int[]{-1,-1};
        if(nums.length == 0||nums[nums.length- 1] < target) return new int[]{-1,-1};

        //然后进行正常情况的处理
        int [] res = new int[]{-1,-1};
        //首先找出数字的左边界 也就是  >= 第一个值
        int left = 0;
        int right = nums.length-1;
        while(left < right){
            int mid = (left + right)/2;
            if(nums[mid] >= target){
                right = mid;
            }else{
                left = mid+1;
            }
        }
        //如果存在 那么就对应的更改值即可
        if(nums[left] == target){
            res[0] = left;
        }

        //然后找出右边界的最后一个
        left = 0;
        right = nums.length-1;
        while(left < right){
            int mid = (left + right+1)/2;
            if(nums[mid] <= target){
                left = mid;
            }else{
                right = mid -1;
            }
        }
        //如果存在 那么就对应的更改值即可
        if(nums[left] == target){
            res[1] = left;
        }
        return res;
    }

搜索二维矩阵

搜索的区间由一维变成了二维，但是整体上还是一个有序的，可以使用二分的做法。
思路一：先确定具体在哪一个区间里面（确定区间的过程也可以使用二分 或者暴力），然后在具体的区间里面在二分寻找值

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        //二维 -- 一维
        //判断特例
        if(matrix == null || matrix[0] == null) return false;
        int level = matrix.length;
        int column = matrix[0].length;
        if(matrix[level-1][column-1] < target) return false;

        //先找存在的行 -- 可以使用二分 也可以使用 暴力遍历
	/*  int i = 0;
        for(;i < level;i++){
            if( matrix[i][0] <=target  && target <= matrix[i][column-1]){
                break;
            }
        }*/
        int left = 0;
        int right = level-1;
        int mid = 0;
        while(left < right){
            mid = (left + right +1)/2;
            if(matrix[mid][0] <= target){
                left = mid;
            }else{
                right = mid-1;
            }
        }
        level = left;
        left = 0;
        right = column-1;
        while(left < right){
            mid = (left + right +1)/2;
            if(matrix[level][mid] <= target){
                left = mid;
            }else{
                right = mid-1;
            }
        }
        return matrix[level][left] == target;
    }
}

**思路二：**不把它当作一个二维数组去处理，而是全部数字平铺，重新排序编号 根据编号 然后转换为具体的下标找到对应的数字
对应的编号转换为下标的方式
行下标 ： 编号/列数
列下标 ： 编号%列数

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
       if(matrix == null || matrix[0].length == 0) return false;
        int level = matrix.length;
        int column = matrix[0].length;
        int left = 0;
        int right = level * column - 1;
        while (left < right){
            int mid = (left +right)/2;
            if(matrix[mid/column][mid % column] >= target){
                right = mid;
            }else {
                left = mid+1;
            }
        }
        //这里跳出的条件是找到的第一个 大于等于target的数字
        return matrix[left/column][left%column] == target;
    }
}

然后是一个上面题目的进阶版本

搜索二维矩阵II

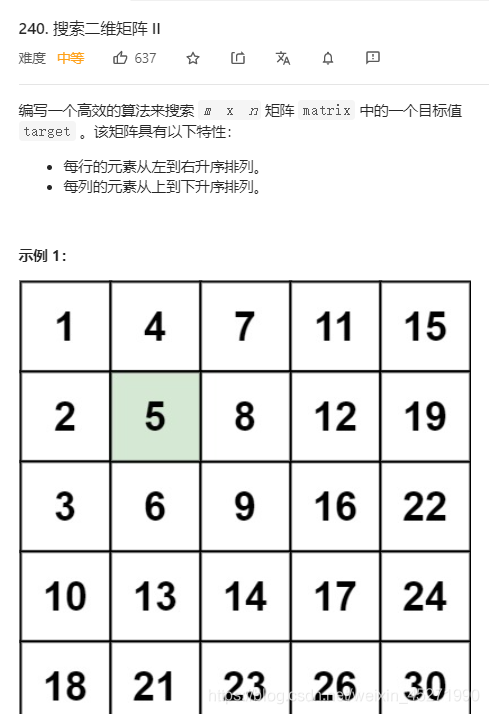
寻找旋转排序数组中的最小值

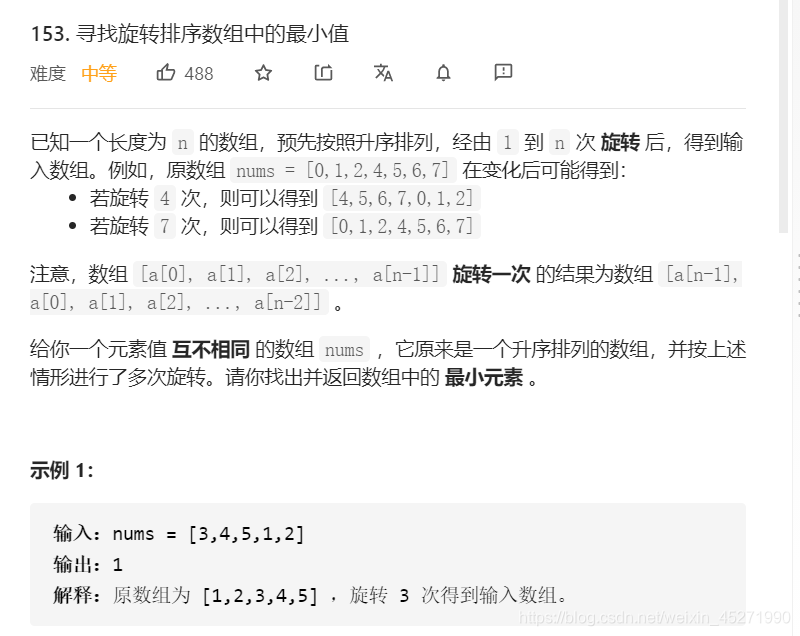
思路一：排序找到最小的哪一个，没什么技术含量

class Solution {
    public int findMin(int[] nums) {
        if(nums == null ) return -1;
        //排序 然后返回第一个
        Arrays.sort(nums);
        return nums[0];

    }
}

思路二：二分，利数组的性质，设计二分函数

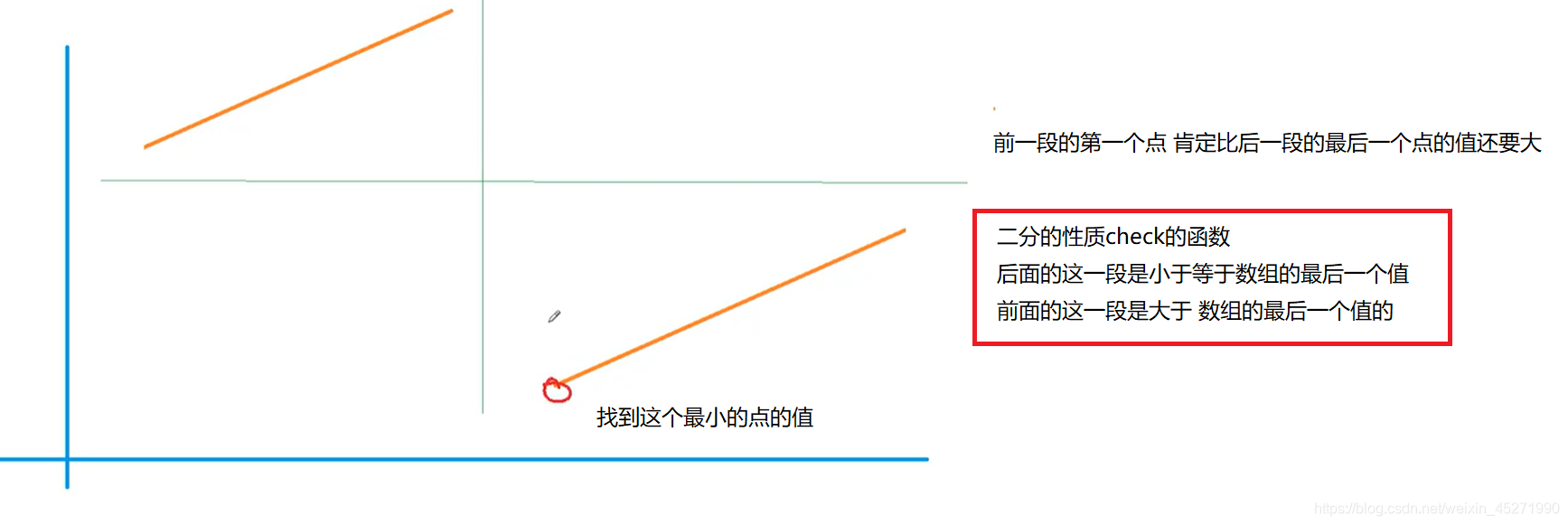
class Solution {
    public int findMin(int[] nums) {
        if(nums == null) return -1;
        int left = 0;
        int right = nums.length-1;
        int target = nums[right];
        int mid = 0;
        while(left < right){
            mid = (left + right)/2;
            if(nums[mid] <= target){
                right = mid;
            }else{
                left = mid+1;
            }
        }
        return nums[left];
    }
}

一个启发
二分是不一定要求整个数组连续递增，只要做到，能够有一个，那么为什么会这样呢？

搜索旋转排序数组

上一个题的进阶版

思考 ：是否可以target 这个值二分整个数组 ？
当然是不可以的 因为整个数组上不存在来连续递增的特性。这个题不可以直接用target进行二分，因为没有单调性，没有办法二段性去使用。

那么上一个题，为什么可以用二分，二分的标准到底是什么？
思路：可以将数组根据最后一个值的大小划分成两段性质，所以需要在这样的基础上 先确定出是在哪一个连续递增的区间上
然后再对应的区间上进行一个二分查找。

class Solution {
    public int search(int[] nums, int target) {
        if (nums == null) return -1;
        int left = 0;
        int right = nums.length;
        int mid = 0;
        int key = nums[nums.length - 1];
        //先二分确定最小值的位置 -- 主要是为了获取最小值下标 之后二分的边界可以确定
        while (left < right) {
            mid = (left + right) / 2;
            if (nums[mid] <= key) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        //然后判断target和 最后一个元素的关系 然后 选择对应的区间进行二分
        if (target > key) {
            //在左区间
            left = 0;
        } else if (target < key) {
            right = nums.length - 1;
        }else {
            return nums.length-1;
        }
        //以最小的值二分的位置作为重新二分的下标

        while (left<right){
            mid = (left+right)/2;
            if(nums[mid] >= target){
                right = mid;
            }else {
                left = mid+1;
            }
        }
        return nums[left]== target? left:-1;
    }
}

宫水三叶的题解

搜索排序数组II

俗话说的是再进阶

第一个错误版本

其实之前找实习的很多笔试题，大概笔试有个三四次，都不是那种直接阐述题目的，都是给你一个小故事，阿里很多大厂都是这样，导致很多笔试，其实第一步难点就是看懂题目到底要干啥。不过也是啊，由现实落地到代码思想的能力不是人人都具备的。

二分的思路，连怎么涉及check函数基本都说清楚了，只是需要注意的就是数字的越界问题，写求解mid的时候换一种写法就好了。

/* The isBadVersion API is defined in the parent class VersionControl.
      boolean isBadVersion(int version); */

public class Solution extends VersionControl {
    public int firstBadVersion(int n) {
        int left = 1;
        int right = n;
        int mid = 0;
        //尽量少的调用一个函数那么其实本质就是搜索比较的次数尽量少 二分
        while(left < right){
            mid = left + (right-left)/2;
            if(isBadVersion(mid) == true){
                right = mid;
            }else{
                left = mid+1;
            }
        }
        return left;
    }
}

寻找峰值

图画清楚了，基本啥清楚了

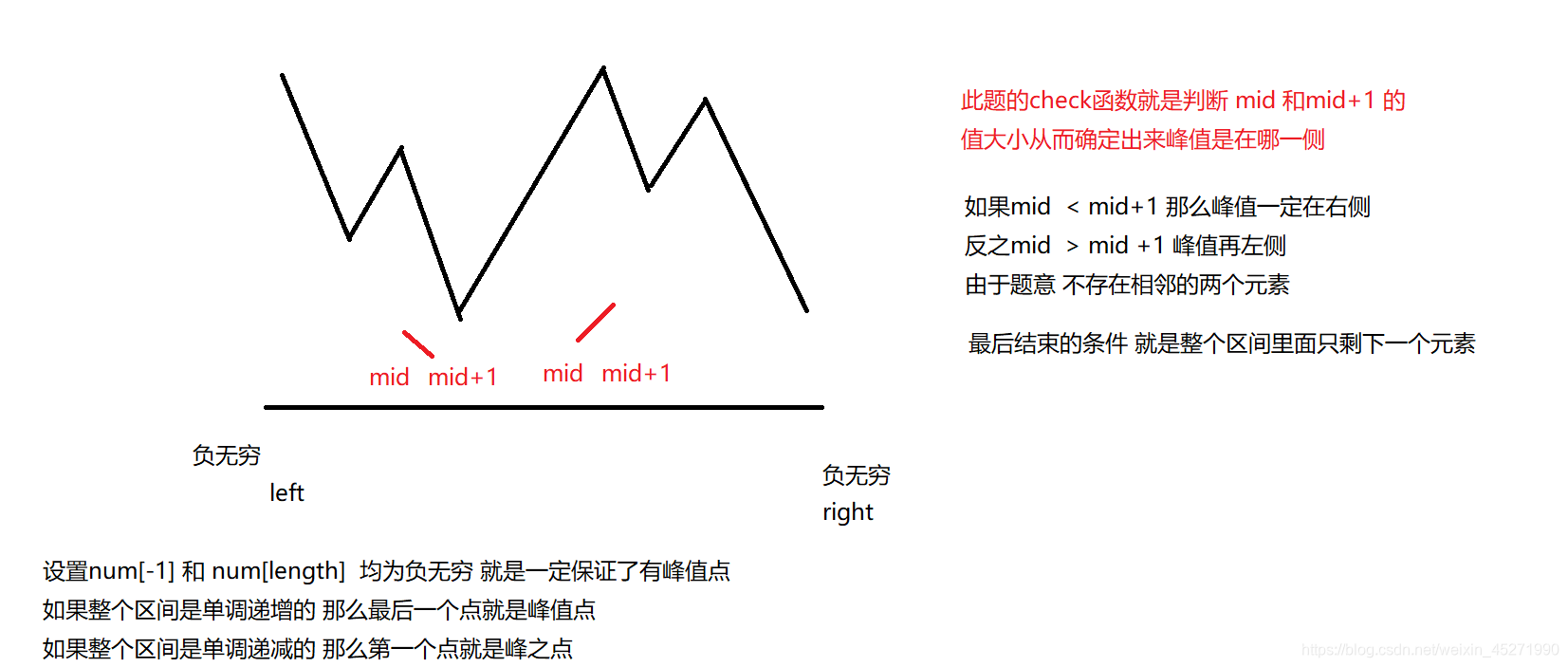
class Solution {
    public int findPeakElement(int[] nums) {
        //最简单的做法 暴力遍历一遍然后求解

        //一旦出现了拐点，那么整个拐点就是峰值
        //但是一定不可能出现越界的问题 如果mid 是边界
        //那么说明left == right 
        //这种情况是不可能进入到循环里面的，所以不会出现越界
        int left = 0;
        int right = nums.length-1;
        int mid =0 ;
        while(left < right){
            mid = (left +right)/2;
            if(nums[mid] < nums[mid+1]){
                left = mid+1;
            }else{
                right = mid;
            }
        }
        return left;
    }
}

寻找重复数

这个题是一个没有一个明确的二段性质的题目，比较不容易想到，主要可以以学习思路为基础。

思路一： 从题目要求不可改变数组，不可以使用额外的空间，可以满足的有两种算法
一个是抽屉原理，一个是判断链表是否有环的思想

使用抽屉原理来思考 苹果个数是大于抽屉个数 那么一定存在一个抽屉里面有两个苹果 也就是说一个数值被两个数组元素同时占有
苹果是说 有n+1个数字 抽屉是说 取值的范围只能在1-n之间

class Solution {
    public int findDuplicate(int[] nums) {
        //常规思路 数组排序之后  进行遍历的两两比较的操作
        //萝卜坑原理 每一个数字放的位置 都应该是数值-1 如果要存放的位置已经是这个数字 那么这个遍历到的数字就是一个重复的数字
        //如果不限制额外的空间 还可以使用 hashmap 计数的方式
        //使用链表判断是否有环的做法来判断
        //抽屉原理
        int left = 1;
        int right = nums.length-1;
        int mid = 0;
        int sub = 0;
        while(left < right){
            mid = (left+right+1)/2;
            sub = mid-left;
            int count = 0;//用来统计数组里面落在左半区间的元素个数
            for(int i =0;i < nums.length;i++){
                if(nums[i] >= left && nums[i] < mid) count++;
            }

            //check函数
            if(count > sub){
                right = mid-1;
            }else{
                left = mid;
            }

        }
        return left;
    }
}

思路二： ；链表有环的思想 （快慢指针）
但是如何设计让数组变成一个可以有环的链表，是这个题的难点
思想的本质是建立了一个映射关系

 /**
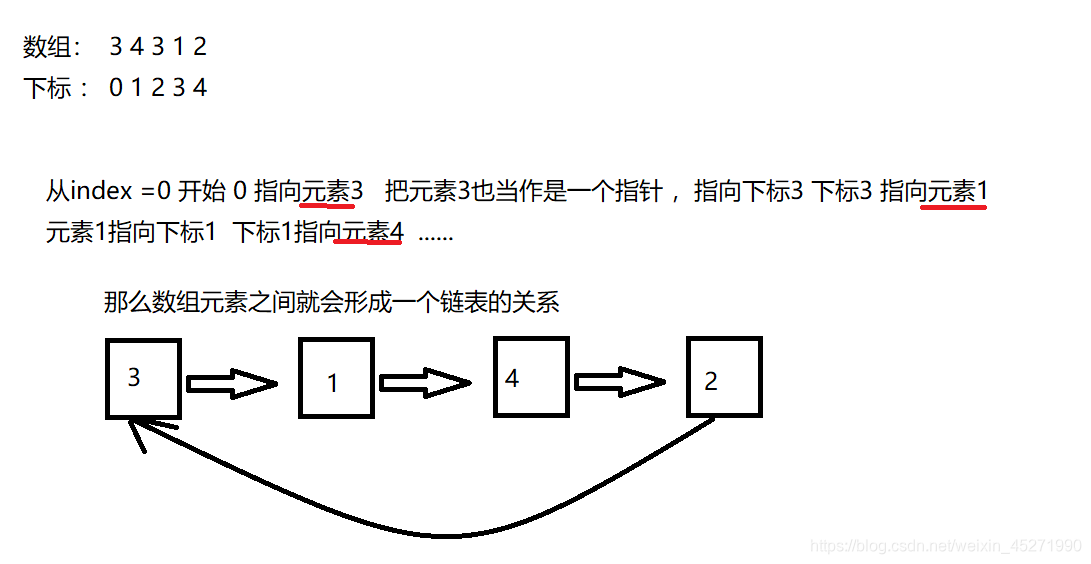
     * 快慢指针
     * 个题目给的特殊的数组当作一个链表来看，
     * 数组的下标就是指向元素的指针，把数组的元素也看作指针。
     * 如 0 是指针，指向 nums[0]，而 nums[0] 也是指针，指向 nums[nums[0]].
     * @param nums
     * @return
     */
    public  static int findDuplicate(int[] nums) {
        //链表有环的思想 快慢指针 一定要把保证的是 有相同的起点，这样才有性质可说
        int slow = 0;
        int fast = 0;
        slow = nums[slow];
        fast = nums[nums[fast]];
        // 这里确实是在相遇
        while(nums[slow] != nums[fast]){
            slow = nums[slow];
            fast = nums[nums[fast]];
        }

        //但是这时候的一个一步走的根本不可能实现 找到重复度额数字
        slow = 0;
        while(nums[slow] != nums[fast]){
            slow = nums[slow];
            fast = nums[fast];
        }

        return nums[slow];
    }

其他可以扩展的，但是不太符合题目的要求
思路三： 萝卜坑原理
思路四”： 最常规的，排序暴力遍历，懒得写代码了。

H指数 II

class Solution {
    public int hIndex(int[] citations) {
        int length = citations.length;
        int left = 0;
        int right = length-1;       
        int mid = 0;
        int count = 0;
        if(length == 0 || citations[length-1] == 0) return 0; 
        while(left < right){
            mid = (left+right)/2;
            count = length-mid; //论文个数
            // 表示的含义是 大于等于mid 的个数 <= mid 那么区间要往左边查找
            if(citations[mid] >= count) right = mid;
            else left = mid+1;
        }
        return length - left;


    }
}

理解题意有一点点的难，但是遵从单调性的
分析单调性：整个数组的元素是代表被引用次数的大小，是遵从单调性的。
求找到的是大于等于当前数组元素的个数是和当前元素的数值相等的。很容易的一个误区会以为最后返回找到的数组元素或者论文的个数是一样的，但是其实不对！！！
对于题中给出的示例比较好理解，几个关键的用例输入的分析
如果数组中最后一个元素都是0 那么说明所有的论文都没有被引用过，所以总共有0篇论文至少被引用了0次


数组元素是100 论文个数是1 这个例子就可以很好的说退出二分循环的时候，返回的论文个数和数组元素不一定相同。
这个示例，h指数应该是1 有1篇论文被至少引用了1次

惨痛的战绩呜呜

关键的关键是分析清楚题意，有点不好理解。

最后，我发现lc里面可以使用二分思想的题真的太多了，上述这写题目根本无法完全涉及到，但是基本上，二分也逃离不出这些题目了。
这是二分的一周，下一周可能会写什么，我也不知道，嘻嘻嘻…