目录
一、原理
????????从一系列有特征和标签的数据中总结出决策规则,通过树状图来呈现,以解决分类和回归问题。
????????一棵树包含一个根节点、若干内部节点和若干叶子节点。叶子节点对应决策结果,其他每个节点对应一个特征测试,特征选择的衡量指标是不纯度。
? ? ? ? 决策树的生成是一个递归过程:
? ? ? ? 计算全部特征的不纯度指标 → 选取不纯度最优的特征进行分支 → 以此类推(直到无更多特征可用或者整体不纯度达到最优) → 停止生长
二、决策树的学习过程?
- 特征选择
- 决策树生成
- 剪枝
?第一步:如何切分特征(选择节点) → 特征选择
? ? ? ? 通过一种衡量标准,来确定最佳节点和最佳分支方法。
? ? ? ? 这个衡量标准就是不纯度?
1. 不纯度的计算方法:信息熵和基尼系数
(1)信息熵
????????从概率统计的角度看,信息熵是对随机变量不确定性的度量,也可以说是对随机变量的概率分布的一个衡量。
? (2)基尼系数
计算速度:信息熵 > 基尼系数(不涉及对数)
敏感性:信息熵 > 基尼系数(信息熵对不纯度更敏感 → 决策树生长更“精细” → 过拟合)
?2. 特征选择方法
?2.1 信息增益(ID3算法)
????????Gain = 父节点信息熵 - 所有子节点信息熵的加权平均(权重是使用单个叶子节点上所占的样本量 比上父节点上的总样本量)
根据信息增益准则的特征选择方法是:对训练数据集(或子集)D,计算其每个特征的信息增益,并比较它们的大小,选择信息增益最大的特征。
ID3算法在每一次对决策树进行分叉选取最优特征时,会选取信息增益最高的特征来作为分裂特征。
缺陷:信息增益准则对可取值数目较多的属性有所偏好。
- 信息增益主要用于帮助选择某个能最大程度减少目标变量不确定性的特征(随机变量),考虑极端情况,当选择唯一id这种随机变量时,会导致条件熵为0,信息增益最大,但这种情况没有任何泛化意义,所以需要对类似的情况进行惩罚,从而帮助我们做出更合理的选择。
?
2.2 信息增益率(C4.5算法)
Gain_ratio = 信息增益 / 特征本身的熵(分支度)
其中,IV(a)为特征的“分支度”,特征a可能取值数目越多 → IV(a)越大
注意:增益率准则对可取值数目较少的特征有所偏好,因此,C4.5算法不是直接选择信息增益率最大的候选划分特征,而是使用了一个启发式:先从候选划分特征中找出信息增益高于平均水平的特征,再从中选择增益率最高的。
2.3 基尼指数(CART算法)
选择使得划分后基尼指数最小的特征作为最优划分特征。
第二步:决策树的生成
? ? ? ? 从根节点出发 →?计算全部特征的不纯度指标 → 选取不纯度最优的特征进行分支 → 以此类推(直到无更多特征可用或者整体不纯度达到最优) → 停止生长
第三步:决策树剪枝
为什么要剪枝:决策树过拟合风险很大,理论上可以完全分得开数据
? ? ? ? (想象一下,如果树足够庞大,每个叶子节点不就一个数据了嘛)
剪枝策略:预剪枝,后剪枝
1. 预剪枝
? ? ? ? 决策树构建过程中,通过设置参数防止树过度生长。
(1)max_depth:限制树的最大深度(一般=3开始尝试)
(2)min_samples_leaf:限制分支后的叶子节点样本数(=5开始或0.5)
(3)min_samples_split:限制节点包含的样本数
(4)max_features:限制特征个数(暴力、不建议)
(5)min_impurity_decrease:限制信息增益大小
2. 后剪枝
? ? ? ? 建完决策树后再剪枝。?
- 先让决策树完整生成一棵大树(过拟合)
- 从下往上以此判断:如果剪掉子树能够提高测试集准确率,那么就剪。
三、决策树的三种算法
1. ID3算法
? ? ? ? 在决策树各个节点上使用信息增益法选择特征,递归的构建决策树。
????????局限性:
????????ID3局限主要源于局部最优化条件,即信息增益的计算方法,其局限性主要有以下几点:
????????(1)分支度越高(分类水平越多)的离散变量往往子节点的总信息熵会更小,ID3是按照某一列进行切分,有一些列的分类可能不会对我需要的结果有足够好的指示。极限情况下取ID作为切分字段,每个分类的纯度都是100%, 因此这样的分类方式是没有效益的
????????(2)不能处理连续型变量 → C4.5可
????????(3)不能处理缺失值 → C4.5可
????????(4)没有剪枝的设置,容易导致过拟合 → C4.5可
2. C4.5算法
2.1 修改局部最优化条件
? ? ? ? 引入分支度来修正信息增益法,使用增益率作为特征选择的参考指标。
????????增益比例是我们决定对哪一列进行分枝的标准,我们分枝的是数字最大的那一列,本质是信息增益最大,分支度又较小的列(也就是纯度提升很快,但又不是靠着把类别分特别细来提升的那些特征)。IV越大,即某一列的分类水平越 多,Gain ratio实现的惩罚比例越大。当然,我们还是希望GR越大越好。
2.2 连续变量处理手段
????????在C4.5中,同样还增加了针对连续变量的处理手段。如果输入特征字段是连续型变量,则有下列步骤:
????????(1)算法首先会对这一列数进行从小到大的排序
????????(2)选取相邻的两个数的中间数作为切分数据集的备选点,若一个连续变量有N个值,则在C4.5的处理过程中将产生 N-1个备选切分点,并且每个切分点都代表着一种二叉树的切分方案,例如:
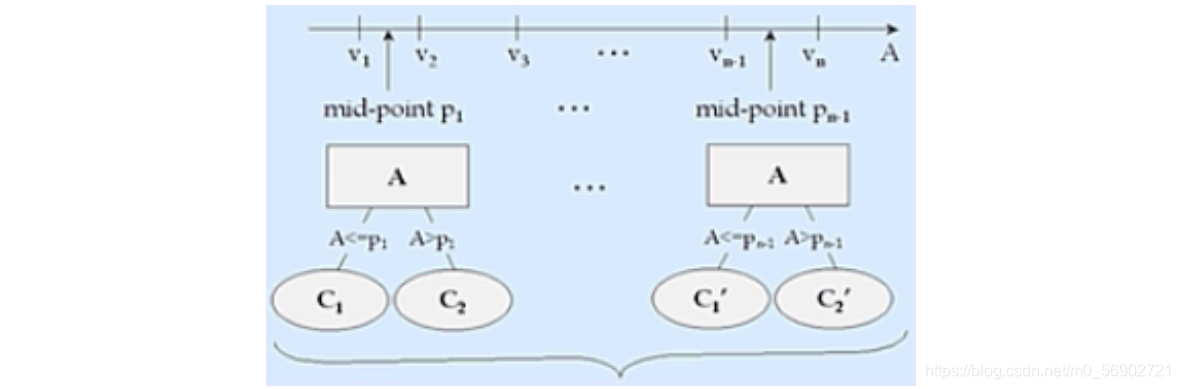
????????这里需要注意的是,此时针对连续变量的处理并非是将其转化为一个拥有N-1个分类水平的分类变量,而是将其转化成了N-1个二分方案,而在进行下一次的切分过程中,这N-1个方案都要单独带入考虑,其中每一个切分方案和一个离散变量的地位均相同(一个离散变量就是一个单独的多路切分方案)。
3. CART算法
? ? ? ? 使用基尼指数作为特征选择的参考指标。
????????目标变量可以是分类型变量也可以是连续型变量,既能做分类,也能做回归。
????????只能是二叉树。
四、决策树的优缺点
????????优点:
????????(1)计算简单、速度快;
????????(2)可解释性强;
????????(3)比较适合处理有缺失属性的样本。
????????缺点:
????????(1)容易发生过拟合(随机森林可以很大程度上减少过拟合);
????????(2)忽略了数据之间的相关性;
????????(3)对于那些各类别样本数量不一致的数据,在决策树当中,信息增益的结果偏向于那些具有更多数值的特征(只要是使用了信息增益,都有这个缺点,如RF)。
五、重要参数

六、交叉验证
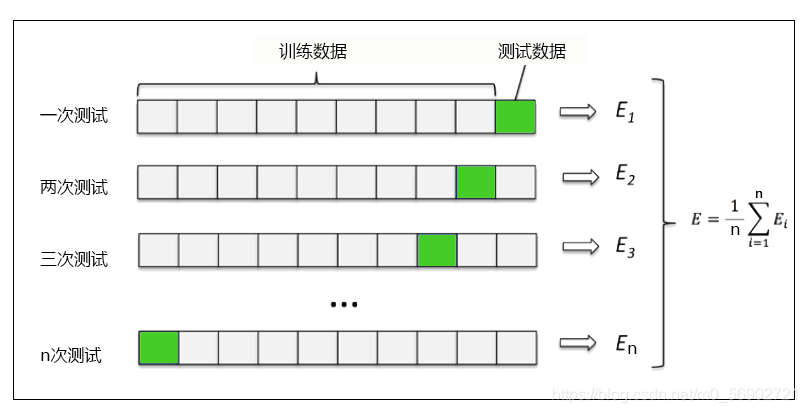
????????交叉验证是用来观察模型的稳定性的一种方法,我们将数据划分为n份,依次使用其中一份作为测试集,其他n-1份作为训练集,多次计算模型的精确性来评估模型的平均准确程度。训练集和测试集的划分会干扰模型的结果,因此用交叉验证n次的结果求出的平均值,是对模型效果的一个更好的度量。
from sklearn.datasets import load_boston
from sklearn.model_selection import cross_val_score
from sklearn.tree import DecisionTreeRegressor
boston = load_boston()
regressor = DecisionTreeRegressor(random_state=0)
cross_val_score(regressor, boston.data, boston.target, cv=10,
scoring = "neg_mean_squared_error")
#交叉验证cross_val_score的用法