强烈推荐,刷PTA的朋友都认识一下柳神–PTA解法大佬
本文由参考于柳神博客写成
还有就是非常非常有用的 算法笔记 全名是
算法笔记 上级训练实战指南 //这本都是PTA的题解算法笔记
PS 今天也要加油鸭

题目原文
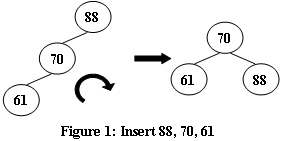
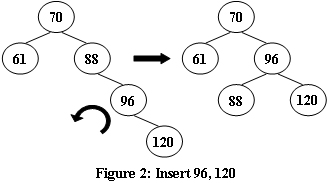
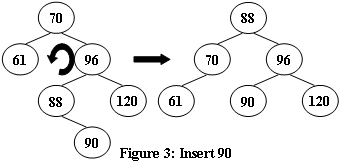
An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.
 |  |
|---|---|
 |  |
Now given a sequence of insertions, you are supposed to output the level-order traversal sequence of the resulting AVL tree, and to tell if it is a complete binary tree.
Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer N (≤ 20). Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.
Output Specification:
For each test case, insert the keys one by one into an initially empty AVL tree. Then first print in a line the level-order traversal sequence of the resulting AVL tree. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line. Then in the next line, print YES if the tree is complete, or NO if not.
Sample Input 1:
5
88 70 61 63 65
Sample Output 1:
70 63 88 61 65
YES
Sample Input 2:
8
88 70 61 96 120 90 65 68
Sample Output 2:
88 65 96 61 70 90 120 68
NO
生词如下:
AVL 平衡二叉树 Adelson-Velsky and Landis Tree
insertions 插入
思路如下:
这题算是比较标准的套模板的题目了
主要就考察,如何构建一颗AVL树(平衡二叉树),只要会构建这题基本就解决了.
就是套用公式吧.
借鉴了算法笔记的代码如下:
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
struct node {
//v是结点权值,height为当前字数高度
int v, height;
//左右孩子的结点地址
node* lchild, * rchild;
};
//生成一个新结点,V为结点权值
node* newNode(int v) {
node* Node = new node; //申请一个node型变量的地址空间
Node->v = v; //结点权值为V
Node->height = 1; //结点高度初始为1
Node->lchild = Node->rchild = nullptr; //初始状态下没有左右孩子
return Node; //返回新建结点的地址
}
//获取以root为根结点的子树的当前height
int getHeight(node* root) {
if (root == nullptr) return 0; //空结点高度为0
return root->height;
}
//计算结点的平衡因子
int getBalanceFactor(node* root) {
//左子树高度减去右子树高度
return getHeight(root->lchild) - getHeight(root->rchild);
}
//更新结点root的height
void updateHeight(node* root) {
//max(右孩子的height,左孩子的height)+1
root->height = max(getHeight(root->lchild), getHeight(root->rchild)) + 1;
}
//左旋
void L(node*& root) {
node* temp = root->rchild;
root->rchild = temp->lchild;
temp->lchild = root;
updateHeight(root);
updateHeight(temp);
root = temp;
}
//右旋
void R(node*& root) {
node* temp = root->lchild;
root->lchild = temp->rchild;
temp->rchild = root;
updateHeight(root);
updateHeight(temp);
root = temp;
}
//插入权值为v的结点
void insert(node*& root, int v) {
if (root == nullptr) { //到达空结点
root = newNode(v);
return;
}
if (v < root->v) {
insert(root->lchild, v);
updateHeight(root);
if (getBalanceFactor(root) == 2) {
if (getBalanceFactor(root->lchild) == 1) { //LL
R(root);
}
else if (getBalanceFactor(root->lchild) == -1) { //LR
L(root->lchild);
R(root);
}
}
}
else { //v比根节点的权值大
insert(root->rchild, v);
updateHeight(root);
if (getBalanceFactor(root) == -2) {
if (getBalanceFactor(root->rchild) == -1) { //RR型
L(root);
}
else if (getBalanceFactor(root->rchild) == 1) { //RL型
R(root->rchild);
L(root);
}
}
}
}
node* Create(int data[], int n) {
node* root = nullptr;
for (int i = 0; i < n; ++i) {
insert(root, data[i]); //将data[0]-data[n-1]插入AVL树中
}
return root;
}
//树的层次遍历
//层次遍历可以用来判断是不是满二叉树
void LayerOrder(node *root) {
queue<node > Q;
node T = *root;
Q.push(*root);
while (!Q.empty()) {
T = Q.front();
Q.pop();
if (T.v != root->v) printf(" ");
printf("%d", T.v);
if (T.lchild) {
Q.push(*T.lchild);
}
if (T.rchild) {
Q.push(*T.rchild);
}
}
}
//判断是不是完全二叉树
bool isCompleteTree(node* root) {
queue<node*>q;
q.push(root);
bool flag = false;
while (!q.empty()) {
auto T = q.front();
q.pop();
if (T == nullptr) {
flag = true;
continue;
}
if (flag) return false;
q.push(T->lchild);
q.push(T->rchild);
}
return true;
}
int main(void) {
node* root = nullptr;
int N,t;
scanf("%d", &N);
for (int i = 0; i < N; ++i) {
scanf("%d", &t);
insert(root, t);
}
LayerOrder(root);
isCompleteTree(root);
if (isCompleteTree(root)) {
printf("\nYES");
}
else {
printf("\nNO");
}
return 0;
}
这题可以算是模板了吧.我个人感觉还是比较经典的.
感觉AVL的代码都差不多,一样的代码,一样的考试.要求会套用.