题目
20. 有效的括号
给定一个只包括 ‘(’,’)’,’{’,’}’,’[’,’]’ 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
示例 1:
输入:s = “()”
输出:true
示例 2:
输入:s = “()[]{}”
输出:true
示例 3:
输入:s = “(]”
输出:false
示例 4:
输入:s = “([)]”
输出:false
示例 5:
输入:s = “{[]}”
输出:true
提示:
1 <= s.length <= 104
s 仅由括号 '()[]{}' 组成
题解:经典的括号匹配问题,用栈处理。
那么这里为什么不用Stack,而使用ArrayDeque呢?因为Stack是Vector的子类,而Vector里面的方法基本都是用synchronized修饰的,虽然是线程安全的,但是效率会比较低,而对于ArrayList和ArrayDeque,本身是线程不安全的,若想要线程安全,只需使用Collections.synchronizedCollection()转化成线程安全的,基本可以绕过Vector。
class Solution {
public boolean isValid(String s) {
char[] sc = s.toCharArray();
ArrayDeque<Character> deque = new ArrayDeque();
for(int i = 0; i < sc.length; i++){
if(sc[i] == '(' || sc[i] == '[' || sc[i] == '{'){
deque.addLast(sc[i]);
}else{
if(deque.isEmpty()){
return false;
}
char c = deque.removeLast();
if((sc[i] == ')' && c != '(' ) || (sc[i] == '}' && c != '{' ) || (sc[i] == ']' && c != '[' ))
return false;
}
}
return deque.isEmpty();
}
}
150. 逆波兰表达式求值
根据 逆波兰表示法,求表达式的值。
有效的算符包括 +、-、*、/ 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
说明:
整数除法只保留整数部分。
给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
示例 1:
输入:tokens = [“2”,“1”,"+",“3”,"*"]
输出:9
解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
示例 2:
输入:tokens = [“4”,“13”,“5”,"/","+"]
输出:6
解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
示例 3:
输入:tokens = [“10”,“6”,“9”,“3”,"+","-11","","/","",“17”,"+",“5”,"+"]
输出:22
解释:
该算式转化为常见的中缀算术表达式为:
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
提示:
1 <= tokens.length <= 104
tokens[i] 要么是一个算符("+"、"-"、"*" 或 "/"),要么是一个在范围 [-200, 200] 内的整数
逆波兰表达式:
逆波兰表达式是一种后缀表达式,所谓后缀就是指算符写在后面。
平常使用的算式则是一种中缀表达式,如 ( 1 + 2 ) * ( 3 + 4 ) 。
该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。
逆波兰表达式主要有以下两个优点:
去掉括号后表达式无歧义,上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
适合用栈操作运算:遇到数字则入栈;遇到算符则取出栈顶两个数字进行计算,并将结果压入栈中。
题解:上面介绍优点的第二个就是题解。
class Solution {
public int evalRPN(String[] tokens) {
ArrayDeque<Integer> deque = new ArrayDeque();
for(int i = 0; i < tokens.length; i++){
if(isNumber(tokens[i])){
deque.addLast(Integer.parseInt(tokens[i]));
}else{
Integer a = deque.removeLast();
Integer b = deque.removeLast();
switch(tokens[i]){
case "+" : deque.addLast(b + a); break;
case "-" : deque.addLast(b - a); break;
case "*" : deque.addLast(b * a); break;
case "/" : deque.addLast(b / a); break;
}
}
}
return deque.removeLast();
}
public boolean isNumber(String str){
return !(str.equals("+") || str.equals("-") || str.equals("*") || str.equals("/"));
}
}
71. 简化路径
给你一个字符串 path ,表示指向某一文件或目录的 Unix 风格 绝对路径 (以 ‘/’ 开头),请你将其转化为更加简洁的规范路径。
在 Unix 风格的文件系统中,一个点(.)表示当前目录本身;此外,两个点 (…) 表示将目录切换到上一级(指向父目录);两者都可以是复杂相对路径的组成部分。任意多个连续的斜杠(即,’//’)都被视为单个斜杠 ‘/’ 。 对于此问题,任何其他格式的点(例如,’…’)均被视为文件/目录名称。
请注意,返回的 规范路径 必须遵循下述格式:
始终以斜杠 '/' 开头。
两个目录名之间必须只有一个斜杠 '/' 。
最后一个目录名(如果存在)不能 以 '/' 结尾。
此外,路径仅包含从根目录到目标文件或目录的路径上的目录(即,不含 '.' 或 '..')。
返回简化后得到的 规范路径 。
示例 1:
输入:path = “/home/”
输出:"/home"
解释:注意,最后一个目录名后面没有斜杠。
示例 2:
输入:path = “/…/”
输出:"/"
解释:从根目录向上一级是不可行的,因为根目录是你可以到达的最高级。
示例 3:
输入:path = “/home//foo/”
输出:"/home/foo"
解释:在规范路径中,多个连续斜杠需要用一个斜杠替换。
示例 4:
输入:path = “/a/./b/…/…/c/”
输出:"/c"
提示:
1 <= path.length <= 3000
path 由英文字母,数字,'.','/' 或 '_' 组成。
path 是一个有效的 Unix 风格绝对路径。
题解:将字符串按照 “/”分隔开,然后遍历,过滤掉空格和“.”,如果是“. .”,并且栈不为空,则出栈;否则入栈。
class Solution {
public String simplifyPath(String path) {
String[] res = path.split("/");
ArrayDeque<String> deque = new ArrayDeque();
for(int i = 0; i < res.length; i++){
if(!res[i].equals("") && !res[i].equals(".")){
if(res[i].equals("..")){
if(!deque.isEmpty())
deque.removeLast();
}else{
deque.addLast(res[i]);
}
}
}
StringBuilder sb = new StringBuilder();
for(String s : deque){
sb.append("/" + s);
}
if(sb.toString().equals(""))
return "/";
return sb.toString();
}
}
144. 二叉树的前序遍历
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
示例 1:
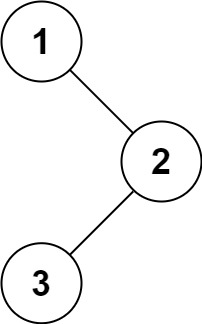
输入:root = [1,null,2,3]
输出:[1,2,3]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
示例 4:
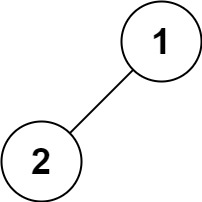
输入:root = [1,2]
输出:[1,2]
示例 5:
输入:root = [1,null,2]
输出:[1,2]
提示:
树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100
进阶:递归算法很简单,你可以通过迭代算法完成吗?
①递归实现:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
List<Integer> res = new ArrayList<>();
public List<Integer> preorderTraversal(TreeNode root) {
if(root != null)
res.add(root.val);
if(root != null && root.left != null)
preorderTraversal(root.left);
if(root != null && root.right != null)
preorderTraversal(root.right);
return res;
}
}
②迭代实现:对于二叉树的前序遍历,可以先推根节点入栈,进入循环,因为栈是后入先出,所以先推入右节点,后推入左节点。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
ArrayDeque<TreeNode> deque = new ArrayDeque<>();
List<Integer> res = new ArrayList<>();
if(root == null)
return res;
deque.addLast(root);
while(!deque.isEmpty()){
TreeNode node = deque.removeLast();
res.add(node.val);
if(node.right != null){
deque.addLast(node.right);
}
if(node.left != null){
deque.addLast(node.left);
}
}
return res;
}
}
94. 二叉树的中序遍历
给定一个二叉树的根节点 root ,返回它的 中序 遍历。
示例 1:
输入:root = [1,null,2,3]
输出:[1,3,2]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
示例 4:
输入:root = [1,2]
输出:[2,1]
示例 5:
输入:root = [1,null,2]
输出:[1,2]
提示:
树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
递归:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
List<Integer> res = new ArrayList<>();
public List<Integer> inorderTraversal(TreeNode root) {
if(root != null && root.left != null)
inorderTraversal(root.left);
if(root != null)
res.add(root.val);
if(root != null && root.right != null)
inorderTraversal(root.right);
return res;
}
}
迭代实现思路:用栈,一路找到二叉树的最左孩子,弹出并存入结果;然后判断当前节点有无右节点,有的话需要继续找到其最左孩子。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
ArrayDeque<TreeNode> deque = new ArrayDeque<>();
List<Integer> res = new ArrayList<>();
if(root == null)
return res;
TreeNode cur = root;
while(!deque.isEmpty() || cur != null){
while(cur != null){
deque.addLast(cur);
cur = cur.left;
}
TreeNode node = deque.removeLast();
res.add(node.val);
if(node.right != null){
cur = node.right;
}
}
return res;
}
}
145. 二叉树的后序遍历
给定一个二叉树,返回它的 后序 遍历。
示例:
输入: [1,null,2,3]
1
2
/
3
输出: [3,2,1]
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
递归:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
List<Integer> res = new ArrayList<>();
public List<Integer> postorderTraversal(TreeNode root) {
if(root != null && root.left != null)
postorderTraversal(root.left);
if(root != null && root.right != null)
postorderTraversal(root.right);
if(root != null)
res.add(root.val);
return res;
}
}
迭代:后序遍历打印的结果是左右中,所以我们入栈的顺序可以是中右左。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
ArrayDeque<TreeNode> deque = new ArrayDeque<>();
ArrayDeque<Integer> resDeque = new ArrayDeque<>();
List<Integer> res = new ArrayList<>();
if(root == null)
return res;
deque.addLast(root);
while(!deque.isEmpty()){
TreeNode node = deque.removeLast();
resDeque.addLast(node.val);
if(node.left != null)
deque.addLast(node.left);
if(node.right != null)
deque.addLast(node.right);
}
while(!resDeque.isEmpty()){
res.add(resDeque.removeLast());
}
return res;
}
}
341. 扁平化嵌套列表迭代器
给你一个嵌套的整型列表。请你设计一个迭代器,使其能够遍历这个整型列表中的所有整数。
列表中的每一项或者为一个整数,或者是另一个列表。其中列表的元素也可能是整数或是其他列表。
示例 1:
输入: [[1,1],2,[1,1]]
输出: [1,1,2,1,1]
解释: 通过重复调用 next 直到 hasNext 返回 false,next 返回的元素的顺序应该是: [1,1,2,1,1]。
示例 2:
输入: [1,[4,[6]]]
输出: [1,4,6]
解释: 通过重复调用 next 直到 hasNext 返回 false,next 返回的元素的顺序应该是: [1,4,6]。
思路:把一个嵌套的列表,存储到普通列表中,然后实现iterator()方法。
/**
* // This is the interface that allows for creating nested lists.
* // You should not implement it, or speculate about its implementation
* public interface NestedInteger {
*
* // @return true if this NestedInteger holds a single integer, rather than a nested list.
* public boolean isInteger();
*
* // @return the single integer that this NestedInteger holds, if it holds a single integer
* // Return null if this NestedInteger holds a nested list
* public Integer getInteger();
*
* // @return the nested list that this NestedInteger holds, if it holds a nested list
* // Return empty list if this NestedInteger holds a single integer
* public List<NestedInteger> getList();
* }
*/
public class NestedIterator implements Iterator<Integer> {
private List<Integer> list;
private Iterator<Integer> cur;
public NestedIterator(List<NestedInteger> nestedList) {
list = new ArrayList<>();
// 把值传入list
DFS(nestedList);
cur = list.iterator();
}
@Override
public Integer next() {
return cur.next();
}
@Override
public boolean hasNext() {
return cur.hasNext();
}
public void DFS(List<NestedInteger> nestedList){
for(NestedInteger i : nestedList){
if(i.isInteger()){
list.add(i.getInteger());
}else{
DFS(i.getList());
}
}
}
}
/**
* Your NestedIterator object will be instantiated and called as such:
* NestedIterator i = new NestedIterator(nestedList);
* while (i.hasNext()) v[f()] = i.next();
*/
102. 二叉树的层序遍历
给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。
示例:
二叉树:[3,9,20,null,null,15,7],

返回其层序遍历结果:
[
[3],
[9,20],
[15,7]
]
题解:这里的ArrayDeque主要的作用是队列了。把每一层的元素入队,然后依次弹出记录。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
Queue<TreeNode> queue = new ArrayDeque<>();
if(root != null){
queue.add(root);
}
while(!queue.isEmpty()){
List<Integer> list = new ArrayList<>();
int n = queue.size();
for(int i = 0; i < n; i++){
TreeNode node = queue.poll();
list.add(node.val);
if(node.left != null)
queue.add(node.left);
if(node.right != null)
queue.add(node.right);
}
res.add(list);
}
return res;
}
}
107. 二叉树的层序遍历 II
给定一个二叉树,返回其节点值自底向上的层序遍历。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
例如:
给定二叉树 [3,9,20,null,null,15,7],
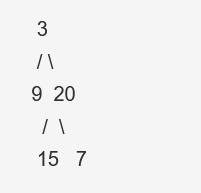
返回其自底向上的层序遍历为:
[
[15,7],
[9,20],
[3]
]
题解:把上一题的数据结构变成LinkedList<>(),用头插法实现倒序。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<List<Integer>> levelOrderBottom(TreeNode root) {
LinkedList<List<Integer>> res = new LinkedList<>();
Queue<TreeNode> queue = new ArrayDeque<>();
if(root != null){
queue.add(root);
}
while(!queue.isEmpty()){
List<Integer> list = new ArrayList<>();
int n = queue.size();
for(int i = 0; i < n; i++){
TreeNode node = queue.poll();
list.add(node.val);
if(node.left != null)
queue.add(node.left);
if(node.right != null)
queue.add(node.right);
}
res.addFirst(list);
}
return res;
}
}
103. 二叉树的锯齿形层序遍历
给定一个二叉树,返回其节点值的锯齿形层序遍历。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
例如:
给定二叉树 [3,9,20,null,null,15,7],
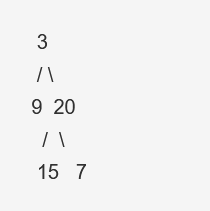
返回锯齿形层序遍历如下:
[
[3],
[20,9],
[15,7]
]
题解:加一个flag判断,当其为偶数行的时候,利用Collections.reverse(),直接反转整一行即可。
class Solution {
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
Queue<TreeNode> queue = new ArrayDeque<>();
if(root != null){
queue.add(root);
}
Boolean flag = false;
while(!queue.isEmpty()){
int n = queue.size();
List<Integer> list = new ArrayList<>();
for(int i = 0; i < n; i++){
TreeNode node = queue.poll();
list.add(node.val);
if(node.left != null)
queue.add(node.left);
if(node.right != null)
queue.add(node.right);
}
if(flag){
Collections.reverse(list);
}
flag = !flag;
res.add(list);
}
return res;
}
}
199. 二叉树的右视图
给定一棵二叉树,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例:
输入: [1,2,3,null,5,null,4]
输出: [1, 3, 4]
解释:

思路:想法很简单,就是层序遍历,然后保存最后一个节点。一开始的代码如下,
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> rightSideView(TreeNode root) {
List<Integer> res = new ArrayList<>();
Queue<TreeNode> queue = new ArrayDeque<>();
if(root != null){
queue.add(root);
}
while(!queue.isEmpty()){
int n = queue.size();
ArrayDeque<Integer> queueLast = new ArrayDeque<>();
for(int i = 0; i < n; i++){
TreeNode node = queue.poll();
queueLast.add(node.val);
if(node.left != null)
queue.add(node.left);
if(node.right != null)
queue.add(node.right);
}
res.add(queueLast.removeLast());
}
return res;
}
}
结果发现效率很低,2ms,只打败20+%的人,参考了一下大佬的代码,发现我这里有一些地方是多余的。
 我只要最后一个元素,却把很多多余的元素给添加进队列了。优化的方法就是把它去掉,然后再for里加一个判断是否为最后一轮遍历,此时的node.val就是最后一个值。变为1 ms, 在所有 Java 提交中击败了99.59% 的用户。
我只要最后一个元素,却把很多多余的元素给添加进队列了。优化的方法就是把它去掉,然后再for里加一个判断是否为最后一轮遍历,此时的node.val就是最后一个值。变为1 ms, 在所有 Java 提交中击败了99.59% 的用户。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> rightSideView(TreeNode root) {
List<Integer> res = new ArrayList<>();
Queue<TreeNode> queue = new ArrayDeque<>();
if(root != null){
queue.add(root);
}
while(!queue.isEmpty()){
int n = queue.size();
for(int i = 0; i < n; i++){
TreeNode node = queue.poll();
if(node.left != null)
queue.add(node.left);
if(node.right != null)
queue.add(node.right);
// 修改的代码
if(i == n - 1){
res.add(node.val);
}
}
}
return res;
}
}
347. 前 K 个高频元素
给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
示例 2:
输入: nums = [1], k = 1
输出: [1]
提示:
1 <= nums.length <= 105
k 的取值范围是 [1, 数组中不相同的元素的个数]
题目数据保证答案唯一,换句话说,数组中前 k 个高频元素的集合是唯一的
进阶:你所设计算法的时间复杂度 必须 优于 O(n log n) ,其中 n 是数组大小。
思路:用一个treeMap来存储数值和它的频数,建立一个优先队列,在维持里面数量为k的情况下,遍历map.keySet。最后输出结果。
import java.util.LinkedList;
import java.util.PriorityQueue;
import java.util.TreeMap;
public class Solution {
class Freq implements Comparable<Freq>{
int e, freq;
public Freq(int e,int freq){
this.e = e;
this.freq = freq;
}
@Override
public int compareTo(Freq another){
if(this.freq < another.freq)
return -1;
else if(this.freq > another.freq)
return 1;
else
return 0;
}
}
public int[] topKFrequent(int[] nums, int k) {
TreeMap<Integer,Integer> map = new TreeMap<>();
for(int num : nums){
if(map.containsKey(num)){
map.put(num, map.get(num) + 1);
}else
map.put(num, 1);
}
PriorityQueue<Freq> pq = new PriorityQueue<>();
for(int key : map.keySet()){
if(pq.size() < k){
pq.add(new Freq(key, map.get(key)));
}else if(map.get(key) > pq.peek().freq){
pq.remove();
pq.add(new Freq(key, map.get(key)));
}
}
int[] res = new int[k];
int i = 0;
while(!pq.isEmpty())
res[i++] = pq.remove().e;
return res;
}
}
23. 合并K个升序链表
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例 1:
输入:lists = [[1,4,5],[1,3,4],[2,6]]
输出:[1,1,2,3,4,4,5,6]
解释:链表数组如下:
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6
示例 2:
输入:lists = []
输出:[]
示例 3:
输入:lists = [[]]
输出:[]
提示:
k == lists.length
0 <= k <= 10^4
0 <= lists[i].length <= 500
-10^4 <= lists[i][j] <= 10^4
lists[i] 按 升序 排列
lists[i].length 的总和不超过 10^4
思路:用容量为K的最小堆优先队列,把链表的头结点都放进去,然后出队当前优先队列中最小的,挂上链表,然后让出队的那个节点的下一个入队,再出队当前优先队列中最小的,直到优先队列为空。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
if(lists.length==0)
return null;
// 定义一个存结果的链表
ListNode dummy = new ListNode(0);
ListNode cur = dummy;
PriorityQueue<ListNode> pq = new PriorityQueue<>(new Comparator<ListNode>(){
@Override
public int compare(ListNode o1,ListNode o2){
return o1.val - o2.val;
}
});
for(ListNode list : lists){
if(list == null)
continue;
pq.add(list);
}
while(!pq.isEmpty()){
ListNode node = pq.poll();
cur.next = node;
cur = cur.next;
if(node.next != null){
pq.add(node.next);
}
}
return dummy.next;
}
}