开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 树形DP -> 正文阅读

[数据结构与算法]树形DP

树形DP

1. 树形DP

定义

在树上进行DP操作。

2. AcWing上的树形DP题目

AcWing 285. 没有上司的舞会

问题描述

问题链接：AcWing 285. 没有上司的舞会

分析

本题相当于让我们每条边上最多选一个点，让选出的点的权值最大。属于最大独立集问题。
分析如下：

在这里插入图片描述

代码

#include <iostream>
#include <cstring>

using namespace std;

const int N = 6010;

int n;
int h[N], e[N], ne[N], idx;
int happy[N];
int f[N][2];
bool has_fa[N];

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void dfs(int u) {
    
    f[u][1] = happy[u];
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        dfs(j);
        
        f[u][1] += f[j][0];
        f[u][0] += max(f[j][0], f[j][1]);
    }
}

int main() {
    
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) scanf("%d", &happy[i]);
    
    memset(h, -1, sizeof h);
    for (int i = 0; i < n - 1; i++) {
        int a, b;
        scanf("%d%d", &a, &b);  // b是a的上司，b向a右一条连边
        add(b, a);
        has_fa[a] = true;
    }
    
    int root = 1;  // 找到根节点
    while (has_fa[root]) root++;
    
    dfs(root);
    
    printf("%d\n", max(f[root][0], f[root][1]));
    
    return 0;
}

AcWing 1072. 树的最长路径

问题描述

问题链接：AcWing 1072. 树的最长路径

分析

树的最长路径也被称为树的直径。
如果树中没有边权，则可以通过如下做法求解树的直径（此时直径为两个点经过的边数）：求两次最远点。
- 任取一点作为起点，找到距离该点最远的一个点u；
- 再找到距离u最远的一点v，那么u、v之间的路径就是一条直径。
本题是有权无向树，我们可以选择任意一个点作为根节点，将整棵树“拎”起来，然后将路径分为若干类，每个点代表一类，每个点代表的集合是经过该点且该点是此路径最高点的所有路径的集合，属性是路径权值和最大值。

在这里插入图片描述

在递归求解的过程中记录每个点所有子树的路径和最大值和次大值（可能相等）即可，最长路径就是两者之和。

代码

#include <iostream>
#include <cstring>

using namespace std;

const int N = 10010, M = N * 2;

int n;
int h[N], e[M], w[M], ne[M], idx;
int ans;

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

int dfs(int u, int father) {  // father是为了防止向回遍历
    
    int d1 = 0, d2 = 0;  // d1: 表示从当前点往下走的最大长度
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == father) continue;
        int d = dfs(j, u) + w[i];
        
        if (d >= d1) d2 = d1, d1 = d;
        else if (d > d2) d2 = d;
    }
    
    ans = max(ans, d1 + d2);
    
    return d1;
}

int main() {
    
    cin >> n;
    
    memset(h, -1, sizeof h);
    for (int i = 0; i < n - 1; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c), add(b, a, c);
    }
    
    dfs(1, -1);  // 任选一点作为根节点均可
    
    cout << ans << endl;
    
    return 0;
}

AcWing 1073. 树的中心

问题描述

问题链接：AcWing 1073. 树的中心

分析

本题记录每个点到子节点的路径的最大值d1和次大值d2，p1记录每个d1对应的路径，p2记录d2对应的路径。
up记录从某个点向其父节点可以到达的最长路径，对于节点x，up[x]存在两种情况：

（1）向父节点u走取得最大值；

（2）达到父节点u后向下折返取得最大值（要求折返路线不能原路返回，即经过x）；

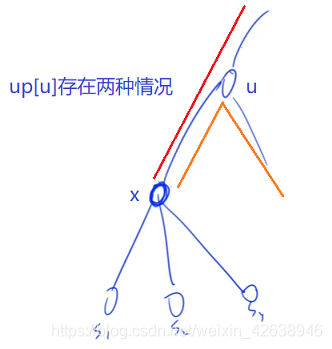
在这里插入图片描述

正是因为不能原路返回，所以要存储每个节点到子节点的路径的次大值d2，注意这里的次大值可能和最大值相同，因为向下可能存在多条路径长度相同的最大值。

代码

#include <iostream>
#include <cstring>

using namespace std;

const int N = 10010, M = N * 2;

int n;
int h[N], e[M], w[M], ne[M], idx;
// d1[u]存储以u为根的子树的高度最大值, d2[u]存储以u为根的子树的次大值（最大值可能等于次大值）
// p1[u]存储最大值路径，如p1[u]=x，说明最大值路径经过(u, x)。
// p2存储次大值路径，在这个题目中没有用，删掉也行，写出来完全是为了对称
// up[u] : 从u向上走的最大长度
int d1[N], d2[N], p1[N], p2[N], up[N];

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

void dfs_d(int u, int father) {
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == father) continue;
        dfs_d(j, u);
        int d = d1[j] + w[i];
        
        if (d >= d1[u]) {
            d2[u] = d1[u], d1[u] = d;
            p1[u] = j;
        } else if (d > d2[u]) d2[u] = d;
    }
}

void dfs_u(int u, int father) {
    for (int i = h[u]; i != -1; i = ne[i]) {
        int j = e[i];
        if (j == father) continue;
        
        if (p1[u] == j) up[j] = max(up[u], d2[u]) + w[i];
        else up[j] = max(up[u], d1[u]) + w[i];
        
        dfs_u(j, u);
    }
}

int main() {
    
    cin >> n;
    
    memset(h, -1, sizeof h);
    for (int i = 0; i < n - 1; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c), add(b, a, c);
    }
    
    dfs_d(1, -1);
    dfs_u(1, -1);
    
    int res = 1e9;
    for (int i = 1; i <= n; i++) res = min(res, max(d1[i], up[i]));
    
    cout << res << endl;
    
    return 0;
}

AcWing 1075. 数字转换

问题描述

问题链接：AcWing 1075. 数字转换

分析

我们使用sum记录每个数的约数之和，按照题意，如果sum[i]<i，可以在sum[i]和i之间建立一条边，因为对于每个i，最多建立一条边，且连接更小的数，因此我们可以得到一个森林。我们求出森林中每棵树的直径即得到本题的答案。
树的直径可以使用AcWing 1072. 树的最长路径的做法。
另外就是求解每个数的约数之和，常规做法是对于给定的数k，按照试除法求出其所有约数，这样的时间复杂度是 $\times \sqrt n)$ 的。我们可以反过来考虑，考虑每个因子i的倍数，这样的时间复杂度是 $\times log(n))$ 的（调和级数）。

代码

#include <iostream>
#include <cstring>

using namespace std;

const int N = 50010;

int n;
int h[N], e[N], ne[N], idx;
int sum[N];  // sum[i]存储i的约数之和
bool st[N];
int ans;

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

int dfs(int u) {
    st[u] = true;

    int d1 = 0, d2 = 0;
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (!st[j]) {
            int d = dfs(j) + 1;
            if (d >= d1) d2 = d1, d1 = d;
            else if (d > d2) d2 = d;
        }
    }

    ans = max(ans, d1 + d2);

    return d1;
}

int main() {

    cin >> n;

    for (int i = 1; i <= n; i++)
        for (int j = 2; j <= n / i; j++)  // 枚举倍数
            sum[i * j] += i;

    memset(h, -1, sizeof h);
    for (int i = 1; i <= n; i++)
        if (sum[i] < i)
            add(sum[i], i);

    for (int i = 1; i <= n; i++)
        if (!st[i])
            dfs(i);

    cout << ans << endl;

    return 0;
}

AcWing 1074. 二叉苹果树

问题描述

问题链接：AcWing 1074. 二叉苹果树

分析

本题是AcWing 10. 有依赖的背包问题问题的一个简化版，区别有两点：（1）本题子树要么没有，要么是两个；（2）本题是保留边，AcWing10是保留点。
使用f[i][j]表示：以i为根且保留j条边最多保留苹果数目。
dfs的过程中，对于某个节点来说，如果其有两个子节点a、b，则物品组有四种组合方式，我们可以依次考虑每棵子树需要保留多少条边，这样就不要枚举a、b有几棵子树了（这样枚举是指数级别的）。
本题解法和AcWing10是一样的，可以参考：背包问题（背包九讲）。

代码

#include <iostream>
#include <cstring>

using namespace std;

const int N = 110, M = N * 2;

int n, m;
int h[N], e[M], w[M], ne[M], idx;
int f[N][N];  // f[i][j]: 以i为根且保留j条边最多保留苹果数目

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

void dfs(int u, int father) {
    for (int i = h[u]; ~i; i = ne[i]) {  // 循环物品组
        if (e[i] == father) continue;
        dfs(e[i], u);
        for (int j = m; j; j--)  // 循环体积
            for (int k = 0; k + 1 <= j; k++)  // 循环决策，即子树占用的边数k
                f[u][j] = max(f[u][j], f[u][j - k - 1] + f[e[i]][k] + w[i]);
    }
}

int main() {
    
    cin >> n >> m;
    memset(h, -1, sizeof h);
    for (int i = 0; i < n - 1; i++) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c), add(b, a, c);
    }
    
    dfs(1, -1);
    
    printf("%d\n", f[1][m]);
    
    return 0;
}

AcWing 323. 战略游戏

问题描述

问题链接：AcWing 323. 战略游戏

分析

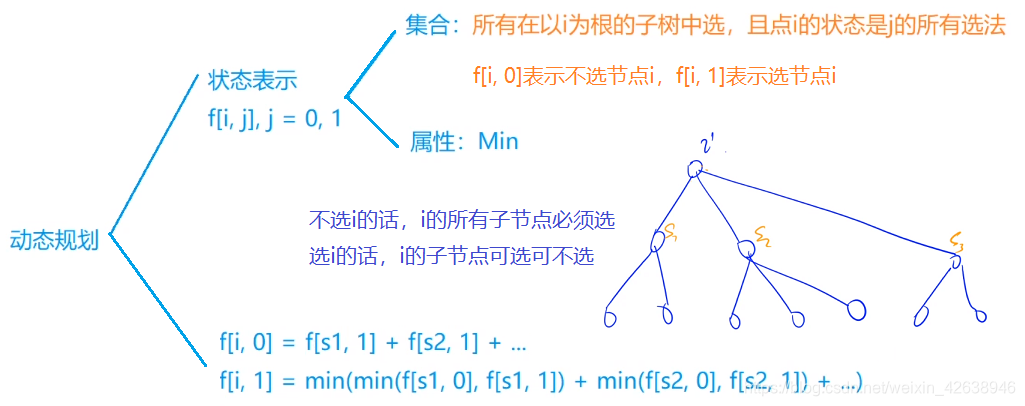
本题相当于问每条边上至少选择一个点，最小的权值和是多少（这里点的权值都为1）？相当于是AcWing 285. 没有上司的舞会的一个对偶问题。对比如下：

（1）没有上司的舞会：每条边上最多选一个点，让选出的点的权值最大。

（2）战略游戏：每条边上最少选择一个点，让选出的点的权值最小。
分析如下：

在这里插入图片描述

本题实际上是一个无向图，从任意一点出发求解结果都是一样的，因此可以用有向图存储，这样可以节省一些空间，但代价是需要找出根节点。
这里采用无向图的写法。

代码

#include <iostream>
#include <cstring>

using namespace std;

const int N = 1510, M = N * 2;

int n;
int h[N], e[M], ne[M], idx;
int f[N][2];

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void dfs(int u, int father) {
    f[u][0] = 0, f[u][1] = 1;
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == father) continue;
        
        dfs(j, u);
        
        f[u][0] += f[j][1];
        f[u][1] += min(f[j][0], f[j][1]);
    }
}

int main() {
    
    while (cin >> n) {
        memset(h, -1, sizeof h);
        idx = 0;
        
        for (int i = 0; i < n; i++) {
            int id, cnt;
            scanf("%d:(%d)", &id, &cnt);
            while (cnt--) {
                int ver;
                scanf("%d", &ver);
                add(id, ver), add(ver, id);
            }
        }
        
        dfs(0, -1);
        
        printf("%d\n", min(f[0][0], f[0][1]));
    }
    
    return 0;
}

AcWing 1077. 皇宫看守

问题描述

问题链接：AcWing 1077. 皇宫看守

分析

注意本题和AcWing 323. 战略游戏的区别，本题在某个点放置一个警卫，则他可以看到周围的点，问所有点都有警卫看守的最少警卫数。AcWing323在某个点放置一个警卫，则他可以看到周围的边，问所有边都有警卫看守的最少警卫数。这两个问题是不同的，例如一排四个点依次相连，本题可以在第一个和最后一个点上放置警卫，但AcWing323这样放置就不满足要求。
状态定义：

f(i, 0): 点i被父节点看到的所有集合对应的最小花费
f(i, 1): 点i被子节点看到的所有集合对应的最小花费
f(i, 2): 在点i上放置警卫的所有摆放方案的最小花费

状态转移（j是i的子节点，k也是i的子节点）：

$\sum min(f(j, 1), f(j, 2)) \\ f(i, 2) = \sum min(f(j, 0), f(j, 1), f(j, 2)) \\ f(i, 1) = \underset {k}{min} \Bigl(f(k, 2) + \underset {j \neq k}{\sum}(f(j, 1), f(j, 2)) \Bigr)$

本题实际上是一个无向图，从任意一点出发求解结果都是一样的，因此可以用有向图存储，这样可以节省一些空间，但代价是需要找出根节点。
这里采用无向图的写法。

代码

#include <iostream>
#include <cstring>

using namespace std;

const int N = 1510, M = N * 2;

int n;
int h[N], e[M], w[N], ne[M], idx;  // w存储节点权值
int f[N][3];

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void dfs(int u, int father) {
    f[u][2] = w[u];  // u放置警卫代价
    
    int sum = 0;
    for (int i = h[u]; i != -1; i = ne[i]) {
        int j = e[i];
        if (j == father) continue;
        
        dfs(j, u);
        
        f[u][0] += min(f[j][1], f[j][2]);
        f[u][2] += min(min(f[j][0], f[j][1]), f[j][2]);
        sum += min(f[j][1], f[j][2]);
    }
    
    f[u][1] = 1e9;
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        f[u][1] = min(f[u][1], f[j][2] + sum - min(f[j][1], f[j][2]));
    }
}

int main() {
    
    cin >> n;
    
    memset(h, -1, sizeof h);
    for (int i = 0; i < n; i++) {
        int id, cost, cnt;
        cin >> id >> cost >> cnt;
        w[id] = cost;
        while (cnt--) {
            int ver;
            cin >> ver;
            add(id, ver), add(ver, id);
        }
    }
    
    dfs(1, -1);  // 任选一点作为根遍历即可
    
    cout << min(f[1][1], f[1][2]) << endl;
    
    return 0;
}

3 LeetCode上一些树形DP问题

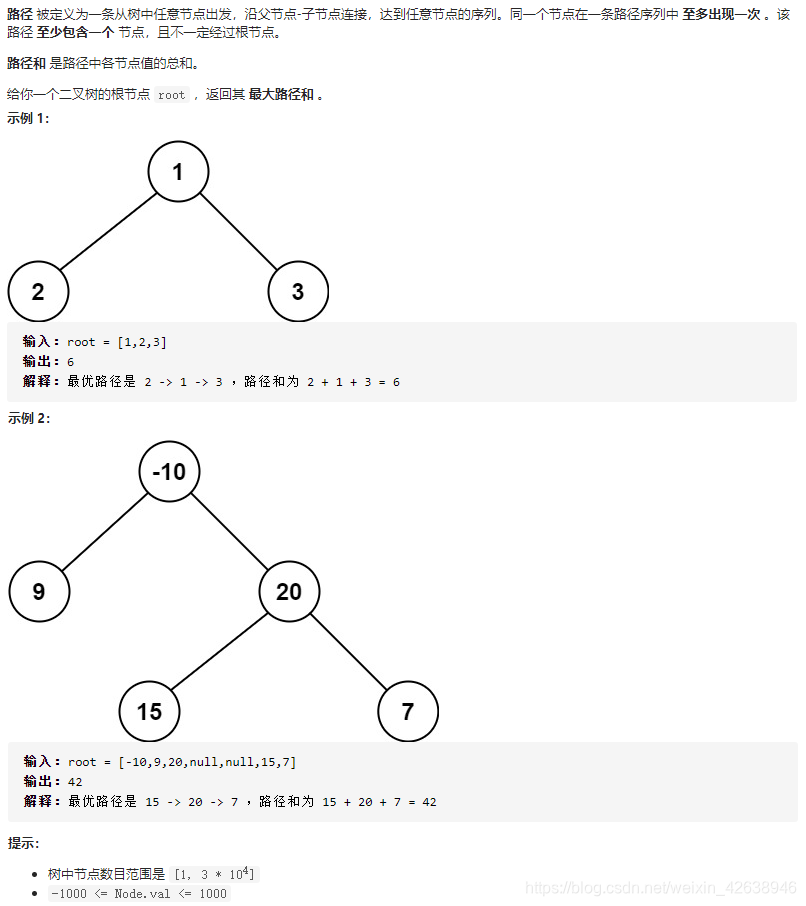
Leetcode 0124 二叉树中的最大路径和

题目描述：Leetcode 0124 二叉树中的最大路径和

在这里插入图片描述

分析

本题的考点：树形DP。
本题就是AcWing 1072. 树的最长路径的简化版。
我们可以枚举路径的最高点节点u，则以u为最高点的所有路径的最大值f(u)是下面三者的最大值：u->val、u->val+f(u->left)、u->val+f(u->right)。如下图：

在这里插入图片描述

得到上述结果后，若令left=max(0, f(u->left))，right=max(0, f(u->right))，则经过u的所有路径中的最大的一个对应的路径和为：u->val+left+right。

代码

class Solution {
public:
    int ans;

    int maxPathSum(TreeNode* root) {
        ans = INT_MIN;
        dfs(root);
        return ans;
    }

    // 返回以u为最高点的所有路径的最大值
    int dfs(TreeNode* u) {
        if (!u) return 0;
        int left = max(0, dfs(u->left)), right = max(0, dfs(u->right));
        ans = max(ans, u->val + left + right);
        return u->val + max(left, right);
    }
};

Java

class Solution {

    int ans = Integer.MIN_VALUE;

    public int maxPathSum(TreeNode root) {
        dfs(root);
        return ans;
    }

    private int dfs(TreeNode u) {
        if (u == null) return 0;
        int left = Math.max(0, dfs(u.left)), right = Math.max(0, dfs(u.right));
        ans = Math.max(ans, u.val + left + right);
        return u.val + Math.max(left, right);
    }
}

时空复杂度分析

时间复杂度： $O (n)$ ，n为树中节点数。
空间复杂度： $O (h)$ ，h为树的高度。

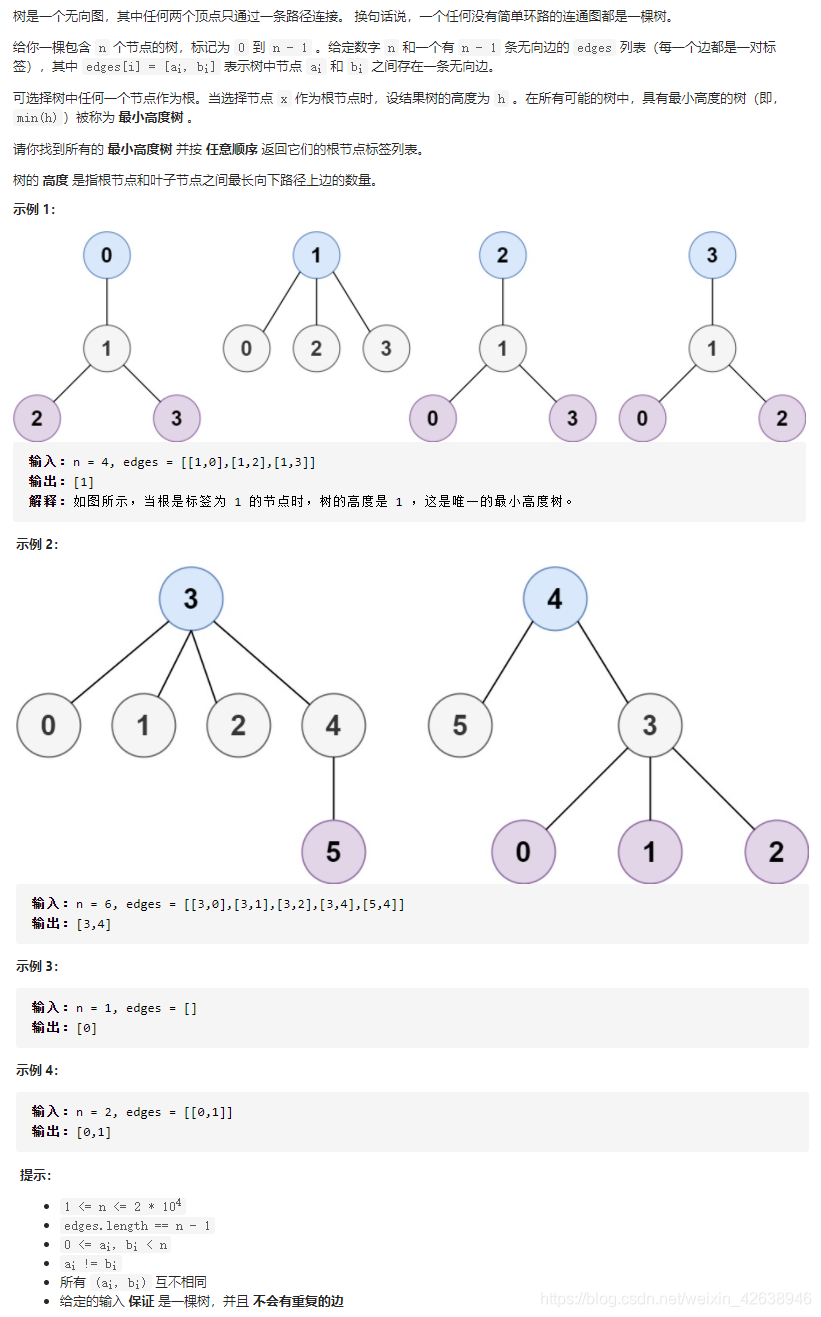
Leetcode 0310 最小高度树

题目描述：Leetcode 0310 最小高度树

在这里插入图片描述

分析

本题的考点：动态规划、树形DP。
本题和AcWing 1073. 树的中心一样。
本题记录每个点到子节点的路径的最大值d1和次大值d2，p1记录每个d1对应的路径，p2记录d2对应的路径。
up记录从某个点向其父节点可以到达的最长路径，对于节点x，up[x]存在两种情况：

（1）向父节点u走取得最大值；

（2）达到父节点u后向下折返取得最大值（要求折返路线不能原路返回，即经过x）；

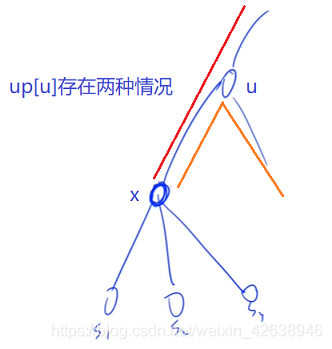
在这里插入图片描述

正是因为不能原路返回，所以要存储每个节点到子节点的路径的次大值d2，注意这里的次大值可能和最大值相同，因为向下可能存在多条路径长度相同的最大值。

代码

class Solution {
public:

    vector<vector<int>> g;
    // d1[u]存储以u为根的子树的高度最大值, d2[u]存储以u为根的子树的次大值（最大值可能等于次大值）
    // p1[u]存储最大值路径，如p1[u]=x，说明最大值路径经过(u, x)。
    // p2存储次大值路径，在这个题目中没有用，删掉也行，写出来完全是为了对称
    // up[u] : 从u向上走的最大长度
    vector<int> d1, d2, p1, p2, up;

    vector<int> findMinHeightTrees(int n, vector<vector<int>> &edges) {

        g.resize(n);
        d1 = d2 = p1 = p2 = up = vector<int>(n);
        for (auto &e : edges) {
            int a = e[0], b = e[1];
            g[a].push_back(b), g[b].push_back(a);
        }

        // 这两句话不能颠倒，因为计算up需要用到down，计算down不需要用到up
        dfs1(0, -1);  // 更新down
        dfs2(0, -1);  // 更新up

        int mind = n + 1;
        for (int i = 0; i < n; i++) mind = min(mind, max(up[i], d1[i]));
        vector<int> res;
        for (int i = 0; i < n; i++)
            if (max(up[i], d1[i]) == mind)
                res.push_back(i);
        return res;
    }

    void dfs1(int u, int father) {
        for (int x : g[u]) {
            if (x == father) continue;
            dfs1(x, u);  // 算出孩子之后，才能计算当前节点
            int d = d1[x] + 1;
            if (d >= d1[u]) {
                d2[u] = d1[u], d1[u] = d;  // 次大值=最大值，最大值=新的最大值
                p2[u] = p1[u], p1[u] = x;
            } else if (d > d2[u]) {
                d2[u] = d;
                p2[u] = x;
            }
        }
    }

    void dfs2(int u, int father) {
        for (int x : g[u]) {
            if (x == father) continue;
            if (p1[u] == x) up[x] = max(up[u], d2[u]) + 1;
            else up[x] = max(up[u], d1[u]) + 1;
            dfs2(x, u);  // 计算父节点之后，才能计算子节点
        }
    }
};

Java

class Solution {

    List<List<Integer>> g = new ArrayList<>();
    int[] d1, d2, p1, p2, up;

    public List<Integer> findMinHeightTrees(int n, int[][] edges) {

        d1 = new int[n]; d2 = new int[n]; p1 = new int[n]; p2 = new int[n]; up = new int[n];
        for (int i = 0; i < n; i++) g.add(new ArrayList<>());
        for (int[] e : edges) {
            int a = e[0], b = e[1];
            g.get(a).add(b); g.get(b).add(a);
        }

        dfs1(0, -1);  // 求d1, d2
        dfs2(0, -1);  // 求up

        int mind = n + 1;
        for (int i = 0; i < n; i++) mind = Math.min(mind, Math.max(d1[i], up[i]));

        List<Integer> res = new ArrayList<>();
        for (int i = 0; i < n; i++)
            if (Math.max(d1[i], up[i]) == mind)
                res.add(i);
        return res;
    }

    private void dfs1(int u, int father) {
        for (int x : g.get(u)) {
            if (x == father) continue;
            dfs1(x, u);
            int d = d1[x] + 1;
            if (d >= d1[u]) {
                d2[u] = d1[u]; d1[u] = d;
                p2[u] = p1[u]; p1[u] = x;
            } else if (d > d2[u]) {
                d2[u] = d;
                p2[u] = x;
            }
        }
    }

    private void dfs2(int u, int father) {
        for (int x : g.get(u)) {
            if (x == father) continue;
            if (p1[u] == x) up[x] = Math.max(up[u], d2[u]) + 1;
            else up[x] = Math.max(up[u], d1[u]) + 1;
            dfs2(x, u);
        }
    }
}

时空复杂度分析

时间复杂度： $O (n)$ ，n为树中节点个数。
空间复杂度： $O (n)$ 。

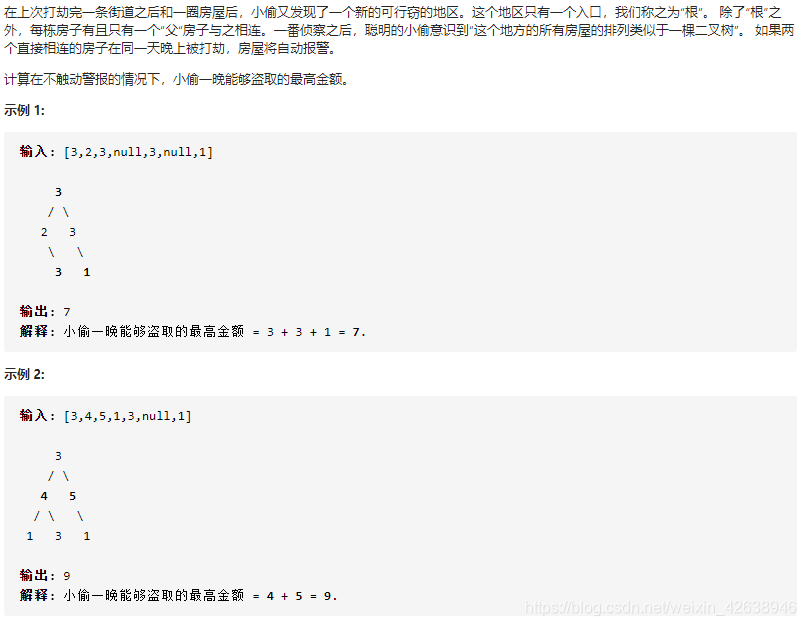
Leetcode 0337 打家劫舍 III

题目描述：Leetcode 0337 打家劫舍 III

在这里插入图片描述

分析

本题的考点：动态规划、树形DP。
本题就是AcWing 285. 没有上司的舞会的简化版。
分析如下：

在这里插入图片描述

代码

class Solution {
public:
    int rob(TreeNode *root) {
        auto f = dfs(root);
        return max(f[0], f[1]);
    }

    vector<int> dfs(TreeNode *u) {
        if (!u) return {0, 0};
        auto x = dfs(u->left), y = dfs(u->right);
        return {max(x[0], x[1]) + max(y[0], y[1]), x[0] + y[0] + u->val};
    }
};

Java

class Solution {
    public int rob(TreeNode root) {
        int[] f = dfs(root);
        return Math.max(f[0], f[1]);
    }

    private int[] dfs(TreeNode root) {
        if (root == null) return new int[]{0, 0};
        int[] x = dfs(root.left), y = dfs(root.right);
        return new int[]{Math.max(x[0], x[1]) + Math.max(y[0], y[1]), x[0] + y[0] + root.val};
    }
}

时空复杂度分析

时间复杂度： $O (n)$ ，n为树中节点数。
空间复杂度：和递归深度有关。

Leetcode 0968 监控二叉树

题目描述：Leetcode 0968 监控二叉树

在这里插入图片描述

分析

本题的考点：动态规划、树形DP。
本题是AcWing 1077. 皇宫看守的简化版，从多叉树变为了二叉树。
状态定义：

f(i, 0): 点i被父节点看到的所有集合对应的最小花费
f(i, 1): 点i被子节点看到的所有集合对应的最小花费
f(i, 2): 在点i上放置警卫的所有摆放方案的最小花费

状态转移（j是i的子节点，k也是i的子节点）：

$\sum min(f(j, 1), f(j, 2)) \\ f(i, 2) = \sum min(f(j, 0), f(j, 1), f(j, 2)) \\ f(i, 1) = \underset {k}{min} \Bigl(f(k, 2) + \underset {j \neq k}{\sum}(f(j, 1), f(j, 2)) \Bigr)$

代码

class Solution {
public:
    const int INF = 1e8;

    vector<int> dfs(TreeNode* root) {
        if (!root) return {0, 0, INF};
        auto l = dfs(root->left), r = dfs(root->right);
        return {
            min(l[1], l[2]) + min(r[1], r[2]),
            min(l[2] + min(r[1], r[2]), r[2] + min(l[1], l[2])),
            min(l[0], min(l[1], l[2])) + min(r[0], min(r[1], r[2])) + 1,
        };
    }

    int minCameraCover(TreeNode* root) {
        auto f = dfs(root);
        return min(f[1], f[2]);
    }
};

Java

class Solution {

    static int INF = (int) (1e8);

    public int minCameraCover(TreeNode root) {
        int[] f = dfs(root);
        return Math.min(f[1], f[2]);
    }

    int[] dfs(TreeNode root) {
        if (root == null) return new int[]{0, 0, INF};
        int[] l = dfs(root.left), r = dfs(root.right);
        return new int[] {
            Math.min(l[1], l[2]) + Math.min(r[1], r[2]),
            Math.min(l[2] + Math.min(r[1], r[2]), r[2] + Math.min(l[1], l[2])),
            Math.min(l[0], Math.min(l[1], l[2])) + Math.min(r[0], Math.min(r[1], r[2])) + 1,
        };
    }
}

Python

class Solution:
    def minCameraCover(self, root: TreeNode) -> int:
        f = self.dfs(root)
        return min(f[1], f[2])
    
    def dfs(self, root):
        if root is None:
            return (0, 0, int(1e8))
        l, r = self.dfs(root.left), self.dfs(root.right)
        return (
            min(l[1], l[2]) + min(r[1], r[2]),
            min(l[2] + min(r[1], r[2]), r[2] + min(l[1], l[2])),
            min(l[0], min(l[1], l[2])) + min(r[0], min(r[1], r[2])) + 1,
        )