目录
一. ID3
1.1 信息增益
???????ID3算法构建决策树的过程简单概括起来就是,自根结点开始,选择信息增益最大的特征作为根结点对应的特征,并依据该特征的可能取值将训练数据分配到不同的子结点,对子结点进行同样的操作,若子结点的所有样本属于同一类别或该子结点处所有特征的信息增益均小于给定阈值或无可供选择的特征,那么这个子结点是一个叶结点,将叶结点的样本数量最多的类别作为叶结点的类别。
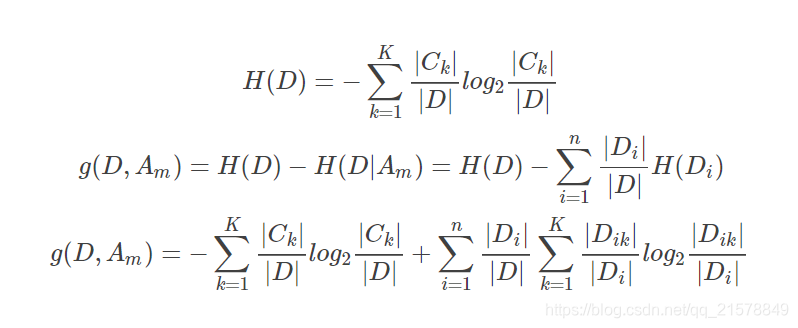
1.2 损失函数
???????通过信息增益特征选择构造的决策树往往能够对训练数据进行很准确的分类,但是应用于测试数据的分类时,效果往往不够理想,造成这种情况的一个重要原因是对训练数据的过拟合,就是过分在意对训练数据分类的准确性,导致模型过于复杂,普适性低,将这样的模型用于测试数据的分类时,效果就大打折扣。解决这个问题的方法是简化模型,剪掉决策树的某些枝,使模型的普适性提高。剪枝的方式是剪掉某些子树或叶结点,并将其父结点做为新的叶结点。要剪掉哪些枝是通过损失函数来确定的,其定义如下。
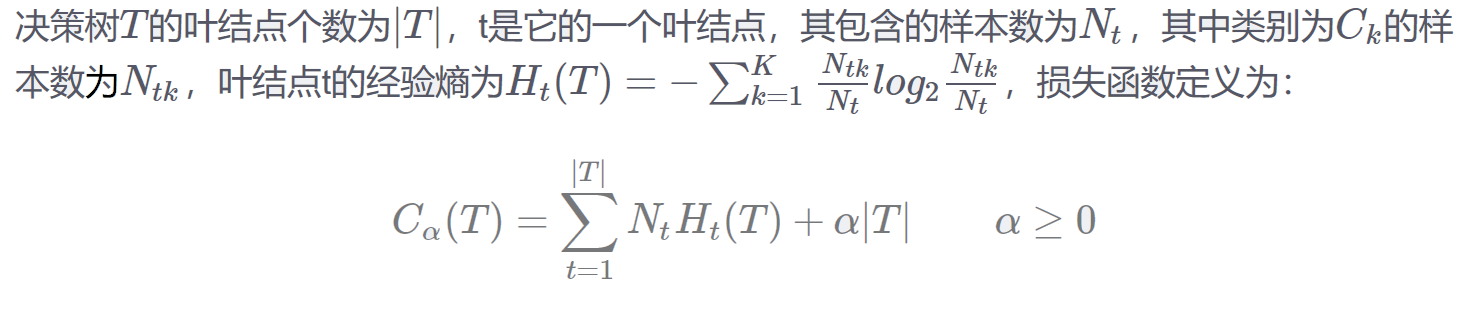
二. C4.5
2.1 信息增益比
???????C4.5算法进行特征选择时不是通过计算信息增益完成的,而是通过信息增益比来进行特征选择。
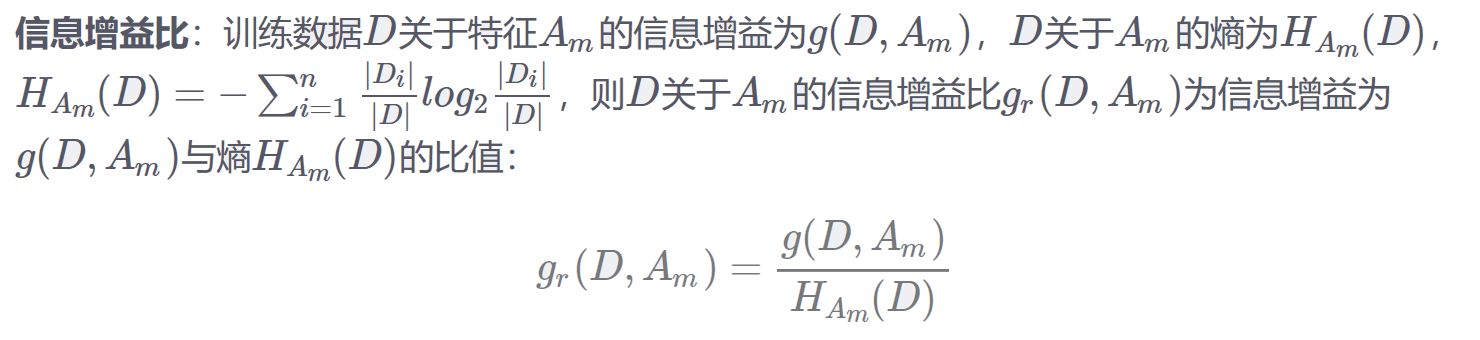
2.2 损失函数
损失函数同ID3
三. CART
CART回归树和CART分类树的建立和预测的区别主要有下面两点:
- 连续值的处理方法不同
- 决策树建立后做预测的方式不同
- 对于连续值的处理,CART分类树采用的是用基尼系数的大小来度量特征的各个划分点的优劣情况。这比较适合分类模型,但是对于回归模型,使用了常见的和方差的度量方式,CART回归树的度量目标是,对于任意划分特征A,对应的任意划分点s两边划分成的数据集D1和D2,求出使D1和D2各自集合的均方差最小,同时D1和D2的均方差之和最小所对应的特征和特征值划分点
- 对于决策树建立后做预测的方式,CART分类树采用叶子节点里概率最大的类别作为当前节点的预测类别。而回归树输出不是类别,它采用的是用最终叶子的均值或者中位数来预测输出结果
3.1 基尼指数(分类树)
???????CART算法构造的是二叉决策树,决策树构造出来后同样需要剪枝,才能更好的应用于未知数据的分类。CART算法在构造决策树时通过基尼系数来进行特征选择。

3.2 损失函数(分类树)

3.3 均方差最小(回归树)
???????CART回归树在构造决策树时通过最小化叶子节点的均方差来进行特征选择。
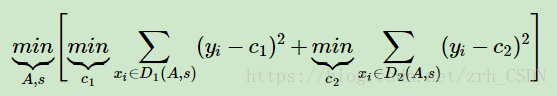
四. 区别