题目描述
有 n 个城市,其中一些彼此相连,另一些没有相连。如果城市 a 与城市 b 直接相连,且城市 b 与城市 c 直接相连,那么城市 a 与城市 c 间接相连。
省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。
给你一个 n x n 的矩阵 isConnected ,其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连,而 isConnected[i][j] = 0 表示二者不直接相连。
返回矩阵中 省份 的数量。
示例 1:
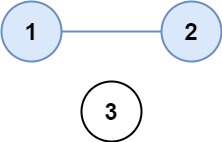
输入:isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出:2示例 2:
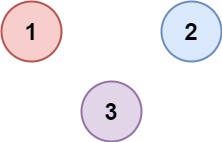
输入:isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出:3提示:
??? 1 <= n <= 200
??? n == isConnected.length
??? n == isConnected[i].length
??? isConnected[i][j] 为 1 或 0
??? isConnected[i][i] == 1
??? isConnected[i][j] == isConnected[j][i]
算法分析
每个城市都属于不同的连通分量。遍历矩阵 isConnected\textit{isConnected}isConnected,如果两个城市之间有相连关系,则它们属于同一个连通分量,对它们进行合并。
遍历矩阵 isConnected的全部元素之后,计算连通分量的总数,即为省份的总数。
代码
class Solution {
public:
vector<int> parent;
vector<int> ranks;
void Init(int n) {
parent.resize(n);
ranks.resize(n, 1);
for(int i = 0; i < n; ++i) {
parent[i] = i;
}
}
int find(int x) {
if(x == parent[x]) {
return x;
}
parent[x] = find(parent[x]);
return parent[x];
}
void merge(int i, int j) {
int rooti = find(i);
int rootj = find(j);
if(ranks[rooti] <= ranks[rootj]) {
parent[rooti] = parent[rootj];
} else {
parent[rootj] = parent[rooti];
}
if(ranks[rooti] == ranks[rootj] && rooti != rootj) {
ranks[rootj]++;
}
}
int findCircleNum(vector<vector<int>>& isConnected) {
const int n = isConnected.size();
Init(n);
for(int i = 0; i < isConnected.size(); ++i) {
for(int j = 0; j < isConnected[0].size(); ++j) {
if(i!=j && isConnected[i][j] == 1) {
merge(i,j);
}
}
}
int ans = 0;
for(int i = 0; i < parent.size(); ++i) {
if(parent[i] == i) {
++ans;
}
}
return ans;
}
};
深度优先搜索
class Solution {
public:
void dfs(vector<vector<int>>& isConnected, vector<bool>& visitor, int i) {
for(int j = 0; j < isConnected[0].size(); ++j) {
if(isConnected[i][j] == 1 && !visitor[j]) {
visitor[j] = true;
dfs(isConnected, visitor, j);
}
}
}
int findCircleNum(vector<vector<int>>& isConnected) {
int n = isConnected.size();
vector<bool> visitor(n, false);
int ans = 0;
for(int i = 0; i < n; ++i) {
if(!visitor[i]) {
dfs(isConnected, visitor, i);
++ans;
}
}
return ans;
}
};
?广度优先搜索
class Solution {
public:
int findCircleNum(vector<vector<int>>& isConnected) {
int n = isConnected.size();
vector<bool> visitor(n, false);
queue<int> que;
int ans = 0;
for(int i = 0; i < n; ++i) {
if(!visitor[i]) {
que.push(i);
while(!que.empty()) {
int cur = que.front();
que.pop();
visitor[cur] = true;
for(int j = 0; j < isConnected[0].size(); ++j) {
if(isConnected[cur][j] == 1 && !visitor[j]) {
que.push(j);
}
}
}
++ans;
}
}
return ans;
}
};
时间复杂度分析
时间复杂度:O(n^2logn),其中 n是城市的数量。需要遍历矩阵 isConnected中的所有元素,时间复杂度是 O(n^2),如果遇到相连关系,则需要进行 2次查找和最多 1 次合并,一共需要进行 n^2次查找和最多n^2次合并,因此总时间复杂度是O(2n^2logn)。这里的并查集使用了路径压缩,但是没有使用按秩合并,最坏情况下的时间复杂度是O(n^2logn),平均情况下的时间复杂度依然是 O(n2α(n)),其中 α\alphaα 为阿克曼函数的反函数,α(n)可以认为是一个很小的常数。
空间复杂度:O(n),其中 n是城市的数量。需要使用数组 parent记录每个城市所属的连通分量的祖先。