六大排序
排序,分为以下几个步骤:取数据->比较数据->交换数据
1.冒泡排序
结构示意图
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Ed8zLKHF-1625758859581)(G:\markdown\C++\数据结构与算法\冒泡排序.PNG)]
最坏排序方式:明明要从小到大排序,结果给的正好是最大到小
第一次:n-1
第二次:n-2
第n-1次:1
————————结果是:1 + 2 + … n-1 = n^2/2 记作为 o(n^2)
————————空间复杂度 0(1);
简单说:进行交换的方式,每次取出最大数据,放到数组最后面。
? 相邻交换的方式。
#include <iostream>
using namespace std;
void printArr(int *begin, int *end)
{
for (int *p = begin; p != end; ++p)
{
cout << *p << " ";
}
cout << endl;
}
void bubble_sort(int *begin, int *end)
{
for (int *p1 = begin; p1 != end; ++p1)
{
for (int *p2 = begin; p2 != end - 1; ++p2)
{
if (*p2 > *(p2 + 1))
{
int temp = *p2;
*p2 = *(p2 + 1);
*(p2 + 1) = temp;
}
}
}
}
int main(int argc, char const *argv[])
{
int arr[] = {6, 2, 3, 5, 4, 7};
bubble_sort(begin(arr), end(arr));
printArr(begin(arr), end(arr));
system("pause");
return 0;
}
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-obk8pYEM-1625758859588)(C:\Users\jialiang.li.v\Desktop\冒泡时间复杂度计算.PNG)]
上面的程序最后的复杂度都是:o(n^2);
那么冒泡能否改进程序,让其最优时间复杂度可以降低.
#include <iostream>
using namespace std;
void printArr(int *begin, int *end)
{
for (int *p = begin; p != end; ++p)
{
cout << *p << " ";
}
cout << endl;
}
void bubble_sort(int *begin, int *end)
{
int count = 0;
bool isContinue = false;
for (int *p1 = begin; p1 != end; ++p1)
{
isContinue = false;
for (int *p2 = begin; p2 != end - 1; ++p2)
{
++count;
if (*p2 > *(p2 + 1))
{
int temp = *p2;
*p2 = *(p2 + 1);
*(p2 + 1) = temp;
isContinue = true; //需要继续排序
}
}
if (isContinue == false)
{
cout << count << endl;
return; //排序完毕
}
}
}
int main(int argc, char const *argv[])
{
int arr[] = {1, 2, 3, 4, 5, 6};
bubble_sort(begin(arr), end(arr));
printArr(begin(arr), end(arr));
system("pause");
return 0;
}
5
1 2 3 4 5 6
请按任意键继续. . .
最佳时间复杂度o(n):
最复杂的时间复杂度是o(n^2);
空间复杂度:o(1)
所以可以知道冒泡排序时间复杂度在o(n)和o(n^2)之间.
2.插入排序
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-h7rrMMJl-1625758859592)(G:\markdown\C++\数据结构与算法\插入排序.PNG)]
简单说:每次的数据与之前比较,一直将最小数据放到第一位。
#include <iostream>
using namespace std;
void printArr(int *begin, int *end)
{
for (int *p = begin; p != end; ++p)
{
cout << *p << " ";
}
cout << endl;
}
void insertSort(int *begin, int *end)
{
for (int *p = begin + 1; p != end; ++p) // 注意begin+1不要写成了begin++
{
for (int *q = p; q != begin; --q)
{
if (*q < *(q - 1)) //找到,则交换,交换之后,需要再次比较
{
int temp = *q;
*q = *(q - 1);
*(q - 1) = temp;
}
else
{
break; //不比前一个小,说明已经插入合适位置
}
}
}
}
int main(int argc, char const *argv[])
{
int arr[] = {6, 2, 3, 5, 4, 7};
insertSort(begin(arr), end(arr));
printArr(begin(arr), end(arr));
system("pause");
return 0;
}
最佳时间复杂度:o(n)
最差时间复杂度:o(n^2)
平均时间复杂度:o(n^2)
3.选择排序
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dv6LPBOd-1625758859598)(G:\markdown\C++\数据结构与算法\选择排序.PNG)]
#include <iostream>
using namespace std;
void printArr(int *begin, int *end)
{
for (int *p = begin; p != end; ++p)
{
cout << *p << " ";
}
cout << endl;
}
void selectSort(int *begin, int *end)
{
for (int *p = begin; p != end; ++p)
{
int *loc = p;
for (int *q = p + 1; q != end; q++)//一直要找到最小的位置
{
if (*q < *loc)
{
loc = q;
}
}
//找到最小值的位置之后,进行交换。
if (loc != p) //地址要不一样,否则是同一个数据
{
int temp = *p;
*p = *loc;
*loc = temp;
}
}
}
int main(int argc, char const *argv[])
{
int arr[] = {6, 2, 3, 5, 4, 7};
selectSort(begin(arr), end(arr));
printArr(begin(arr), end(arr));
system("pause");
return 0;
}
优点:减少了交换的次数,
但是时间复杂度最好和最坏都是o(n^2);
空间复杂度:o(1)
4.希尔排序
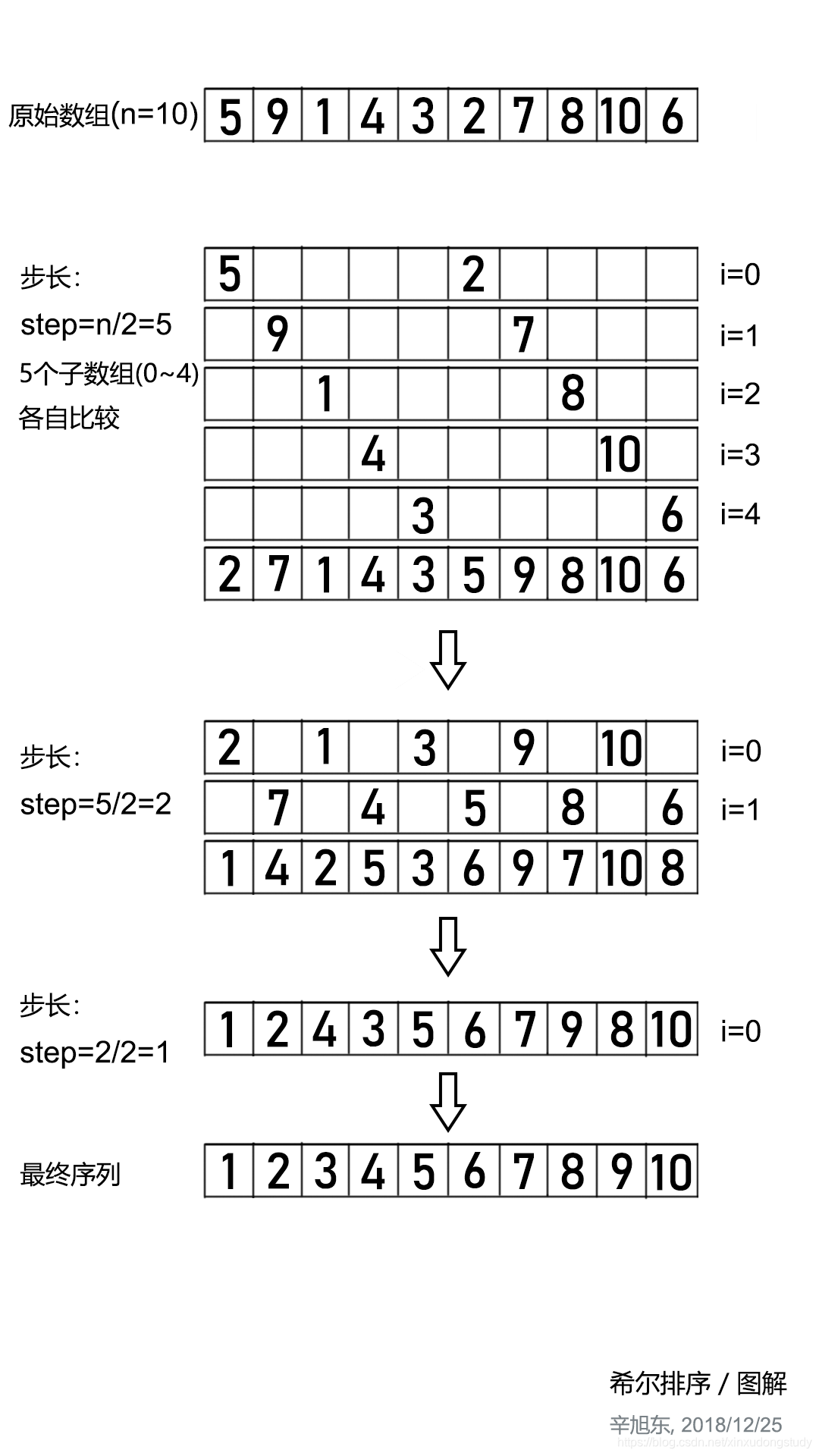
(G:\markdown\C++\数据结构与算法\希尔排序示意图.PNG)]
时间复杂度:O(nlogn)~O(n2),平均时间复杂度大致是O(n√n)
时间复杂度不同
N^1.3是一个比较快的实现
#include <iostream>
using namespace std;
void printArr(int *begin, int *end)
{
for (int *p = begin; p != end; ++p)
{
cout << *p << " ";
}
cout << endl;
}
void hillSort(int *begin, int *end)
{
int size = end - begin;
cout << size << endl;
int gap = size / 2 + size % 2;
while (gap >= 1)
{
for (int *p = begin + gap; p != end; ++p)
{
for (int *q = p; q - gap >= begin; q -= gap) //q-gap不能超过begin值,否则找不到
{
if (*q < *(q - gap))
{
int temp = *q;
*q = *(q - gap);
*(q - gap) = temp;
}
else
{
break;
}
}
}
gap = gap / 2;
}
}
int main(int argc, char const *argv[])
{
// int arr[] = {6, 2, 3, 5, 4, 7};
int arr[] = {0, 40, 30, 8, 10, 20, 50, 3};
// int arr[] = {2, 5, 8, 7, 9, 3};
hillSort(begin(arr), end(arr));
printArr(begin(arr), end(arr));
// int size = sizeof(arr) / sizeof(*arr);
// cout << size << endl;
system("pause");
return 0;
}
java希尔排序
package com.company.sort;
import java.util.Arrays;
public class HillSort {
public static void sort(Comparable[] arr) {
int h = 1;
while (h < arr.length / 2) { // 5
h = 2 * h + 1;
}
System.out.println(h);
System.out.println(h);
while (h > 0) {
for (int i = h; i < arr.length; i++) {
for (int j = i; j >= h; j -= h) {
if (greater(arr[j - h], arr[j])) {
exchange(arr, j - h, j);
} else {
break;
}
}
}
h /= 2;
}
}
public static boolean greater(Comparable v, Comparable w) {
return v.compareTo(w) > 0;
}
public static void exchange(Comparable[] arr, int i, int j) {
Comparable temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
public static void main(String[] args) {
Comparable[] arr = {2, 5, 8, 7, 9, 3};
sort(arr);
System.out.println(Arrays.toString(arr));
}
}
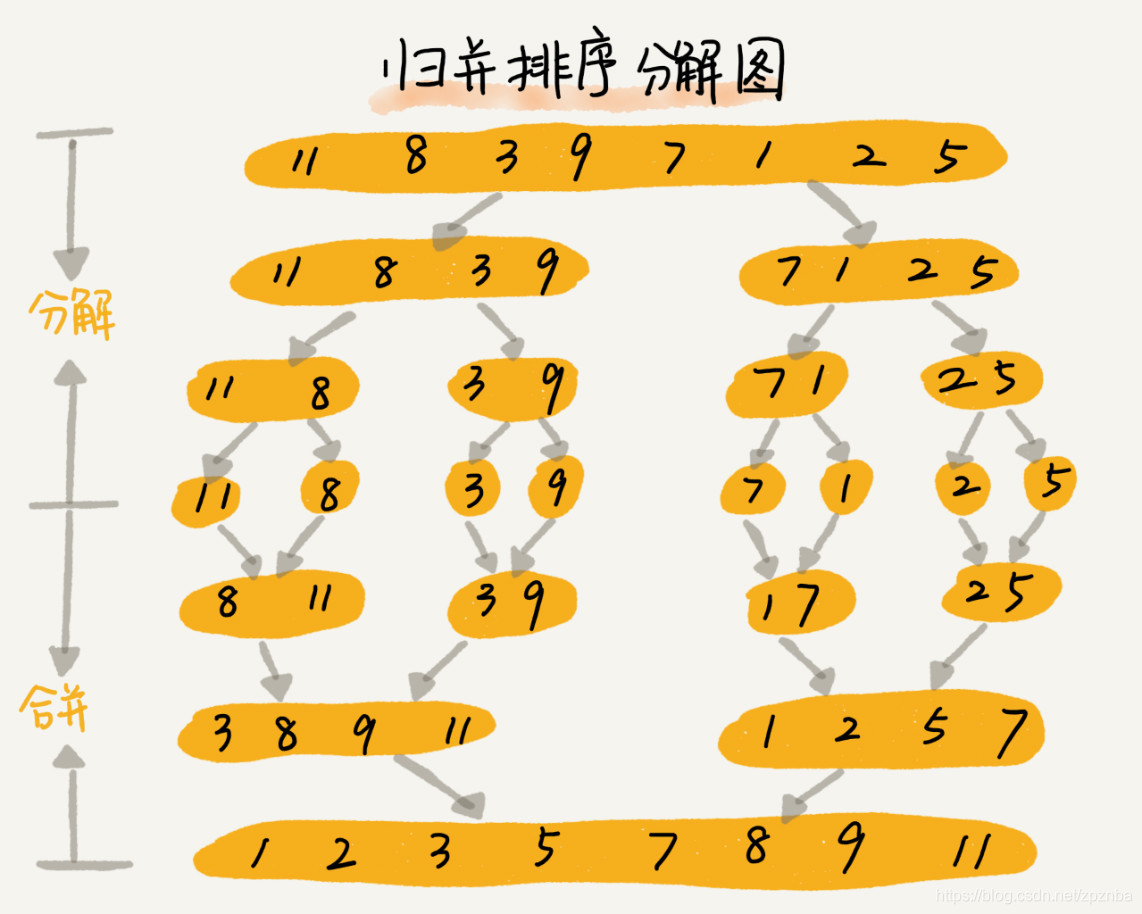
5.归并排序
归并的思路(分治)是把一个大问题a拆解成两个小问题b和c,解决了两个子问题再整合一下,就解决了原问题。用递归的方法,先分解再合并(分治是一种解决问题的处理思想,递归是一种编程技巧,这两者并不冲突):
System.out.println(Arrays.toString(arr));
}
}
### 5.归并排序
归并的思路(分治)是把一个大问题a拆解成两个小问题b和c,解决了两个子问题再整合一下,就解决了原问题。用递归的方法,先分解再合并(分治是一种解决问题的处理思想,递归是一种编程技巧,这两者并不冲突):
