- 2021-7-10 更新:简单(202、217);待更新:中等(137、287)
- 2021-7-8 更新:简单(26、136、剑指3)
难度:简单
26. 删除有序数组中的重复项
| 难度 | 简单 | 通过率 | 54.01%(718,156/1,329,468) |
|---|
题目描述:
给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。
不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以「引用」方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
// nums 是以“引用”方式传递的。也就是说,不对实参做任何拷贝 int len = removeDuplicates(nums); // 在函数里修改输入数组对于调用者是可见的。 // 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。 for (int i = 0; i < len; i++) { print(nums[i]); }
示例 1:
输入:nums = [1,1,2]
输出:2, nums = [1,2]
解释:函数应该返回新的长度 2 ,并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。
示例 2:
输入:nums = [0,0,1,1,1,2,2,3,3,4]
输出:5, nums = [0,1,2,3,4]
解释:函数应该返回新的长度 5 , 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。
提示:
- 0 <=
nums.length<= 3 ? 1 0 4 3 * 10^4 3?104 -
?
1
0
4
-10^4
?104 <=
nums[i]<= 1 0 4 10^4 104 nums已按升序排列
题解
双指针、原地算法
题目已经明确规定“原地修改数组”,那只能在现有数组上进行操作。
双指针是个不错的方法,具体过程看我的手稿,如下图:

值得注意的是if(j-index>1)这句判断,看注释,就知道为什么我要加上这句,当然不这么做也没问题,只是多少有点时间开销,或许这开销也不明显,但是这个小细节优化还是挺到位的哈哈~
class Solution {
public int removeDuplicates(int[] nums) {
int index = 0;
for (int j = 1; j < nums.length; j++)
if (nums[index] != nums[j]) {
// 加上这个判断是对付含有较多连续递增的子数组
// 如[0,1,2,4,5,5,6,7,8,8,9]等
// 当nums[index]!=nums[j]时,会原地复制nums[j]
// 这是个没必要的操作,会有时间开销
if (j - index > 1)
nums[index+1] = nums[j];
++index;
/** 如果优先++index的话,就不用if(j-index>1)了
++index;
nums[index] = nums[j];
*/
}
return index + 1; // index为原地操作的次数,所以最后要+1
}
}
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( 1 ) O(1) O(1)
136. 只出现一次的数字
| 难度 | 简单 | 通过率 | 71.64%(431,981/602,961) |
|---|
题目描述:
给定一个 非空 整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
实例 1:
输入: [2,2,1]
输出: 1
实例 2:
输入: [4,1,2,1,2]
输出: 4
题解
① Set 不可重复性
Set的特性:元素不可重复性
利用这个特性,能快速解决这个问题,当被add()入Set的元素是重复元素时,不进行add()并且将重复元素从set中移除,重复上述操作,最后set中剩下的就是不重复的元素了。
class Solution {
public int singleNumber(int[] nums) {
Set<Integer> set = new HashSet<>();
for (int i = 0; i < nums.length; i++)
// 尝试将当前元素加入 set
if (!set.add(nums[i]))
// 当前元已经存在于 set,即当前元素第二次出现,从 set 删除
set.remove(nums[i]);
// 最后只剩一个不重复的元素
return set.iterator().next();
}
}
时间复杂度: O ( n ) O(n) O(n),达到题目说明的“线性时间复杂度”。
空间复杂度: O ( n ) O(n) O(n) ,使用了
Set空间,未能达到说明中的“可以不使用额外空间”。
② 位运算
既然题目说明中让我们“可以不使用额外空间”,我再想想别的方法——位运算!
为什么是“
位运算”呢?因为题目描述中说到“除了某个元素只出现一次以外,其余每个元素均出现两次”,这是个突破口。
首先,来看个例子,比如:a^b
假设,a、b的值分别是15、2,
a 的值是15,转换成二进制为 1111,
b 的值是2,转换成二进制为 0010,
这下可以根据 异或 的运算规律,可以得出其结果为 1101,即13。
15^2=13
1 1 1 1
⊕ 0 0 1 0
————————————
1 1 0 1
继续看看,我们来看看异或运算⊕的运算性质:
a⊕0 = aa⊕a = 0a⊕b⊕a = (a⊕a)⊕b = 0⊕b = b
回到这题目来,能肯定的是题目提供的数组,其元素个数一定是奇数个!
现在我假设一共有 2m+1 个元素,
其中,m对元素是成对出现的,唯一1个元素就是将被输出的结果。
接下来可以根据这个假设,列出这个表达式:
( a 1 ? a 2 ? ? ? ? ? a m ) ? ( a 1 ? a 2 ? ? ? ? ? a m ) ? a m + 1 ? ( a 1 ? a 1 ) ? ( a 2 ? a 2 ) ? ? ? ? ( a m ? a m ) ? a m + 1 ? 0 ? 0 ? ? ? ? ? 0 ? a m + 1 ? a m + 1 \left ( a_{1} \bigoplus a_{2} \bigoplus \cdot \cdot \cdot \bigoplus a_{m} \right ) \bigoplus \left ( a_{1} \bigoplus a_{2} \bigoplus \cdot \cdot \cdot \bigoplus a_{m} \right ) \bigoplus a_{m+1} \\ \Rightarrow \left ( a_{1} \bigoplus a_{1} \right ) \bigoplus \left ( a_{2}\bigoplus a_{2} \right ) \bigoplus \cdot \cdot \cdot \left ( a_{m}\bigoplus a_{m} \right ) \bigoplus a_{m+1} \\ \Rightarrow 0 \bigoplus 0 \bigoplus \cdot \cdot \cdot \bigoplus 0 \bigoplus a_{m+1} \\ \Rightarrow a_{m+1} (a1??a2??????am?)?(a1??a2??????am?)?am+1??(a1??a1?)?(a2??a2?)????(am??am?)?am+1??0?0?????0?am+1??am+1?
class Solution {
public int singleNumber(int[] nums) {
// (a1?⊕a1?)⊕(a2?⊕a2?)⊕?⊕(am?⊕am?)⊕am+1?
// ? 0⊕0⊕?⊕0⊕am+1?=am+1?
// 结合三个性质:
// 1、a⊕0 = a
// 2、a⊕a = 0
// 3、a⊕b⊕a = (a⊕a)⊕b = 0⊕b = b
int ans = 0;
for(int num : nums){
// 比如:a^b=13
// a 的值是15,转换成二进制为1111,
// b 的值是2,转换成二进制为0010,
// 根据异或的运算规律,可以得出其结果为1101,即13
ans ^= num;
}
return ans;
}
}
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( 1 ) O(1) O(1),明显达到了说明中的“不使用额外空间”
Stream流,一行实现 位运算 操作
- 这种过于高级,使用的是Java的Stream API,看看就好~
class Solution {
public int singleNumber(int[] nums) {
return Arrays.stream(nums).reduce((a,b)->a^b).getAsInt();
}
}
③ 双指针
双指针,也是一种解决办法,思路就不码字了,直接看代码理解吧 ~
class Solution {
public int singleNumber(int[] nums) {
int len = nums.length;
if (len == 1) return nums[0];
int index = 0;
Arrays.sort(nums);
for (int i = 1; i < len-1; i = i+2) {
if (nums[i] == nums[i-1])
index = index + 2;
else if (nums[i] != nums[i-1])
return nums[i-1];
else if (index == len-1)
return nums[index];
}
return nums[index];
}
}
④ List集合
- 创建一个集合,遍历数组,集合中没有遍历的元素就直接添加,如果有就把集合中元素删除。
class Solution {
public int singleNumber(int[] nums) {
List<Integer> list = new ArrayList<>();
for (int i = 0; i < nums.length; i++) {
if (!list.contains(nums[i])){
list.add(nums[i]);
}else {
list.remove((Integer) nums[i]);
}
}
return list.get(0);
}
}
⑤ 数组排序
- 这也能做到“不适用额外空间”,但是性能会低一些,作为了解吧~
class Solution {
/* 排序1 */
public int singleNumber_sort_1(int[] nums) {
int len = nums.length;
if (len == 1) return nums[0];
int index = 0;
Arrays.sort(nums);
for(int i = 0; i < len; i += 2)
if(i == len-1 || nums[i] != nums[i+1])
return nums[i];
return -1;
}
}
class Solution {
/* 排序2 */
public int singleNumber_sort_2(int[] nums) {
int len = nums.length;
if (len == 1) return nums[0];
int index = 0;
Arrays.sort(nums);
for (int i = 1; i < len; i += 2) {
if (nums[i] == nums[i-1])
index += 2;
else if (nums[i] != nums[i-1])
return nums[i-1];
else if (index < len)
return nums[index];
}
return nums[index];
}
}
202. 快乐数
| 难度 | 简单 | 通过率 | 61.55%(150,223/244,049) |
|---|
编写一个算法来判断一个数 n 是不是快乐数。
「
快乐数」定义为:对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为1,也可能是无限循环但始终变不到1。
如果可以变为 1,那么这个数就是快乐数。
如果n是快乐数就返回true;不是,则返回false。
示例 1:
输入:19
输出:true
解释:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
示例 2:
输入:n = 2
输出:false
提示:
- 1 <=
n<= 2 31 ? 1 2^{31} - 1 231?1
题解
- 可以用“
哈希集合”或者“递归”来实现,但更建议用“快慢指针”,更好理解!- 不建议用集合记录每次的计算结果来判断是否进入循环,因为这个集合可能大到无法存储。
- 同理,也不建议使用递归,如果递归层次较深,会直接导致调用栈崩溃。
- 看了官方题解后发现这其实是道数学题,可以利用数学的方式来解决:
- 在转换的过程中,会发现一个循环,很关键的循环:
4 → 16 → 37 → 58 → 89 → 145 → 42 → 20 → 4,根据这个循环,其他数字只有两种可能:要么进入这个循环、要么进入1的链。
- 在转换的过程中,会发现一个循环,很关键的循环:
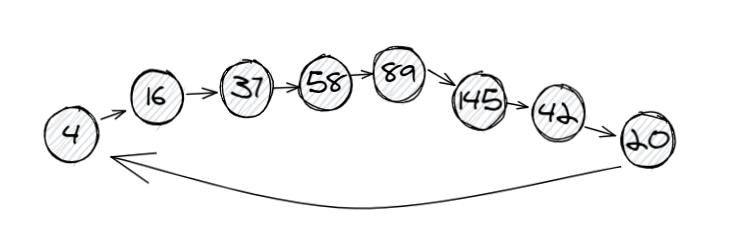
快慢指针
- 把转换过程中的每一个数看作(模拟的)单链表的一个节点,把
1看作单链表的最后一个节点 - 在转换的过程中,快指针一定会追上慢指针,就是快慢指针相等
- 判断快慢指针的值:
- 若
!1,则n不是快乐数,如116 - 若
=1,则n是快乐数,如19
- 若
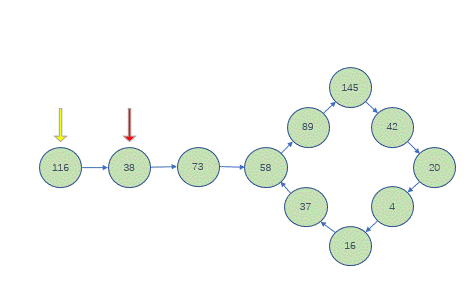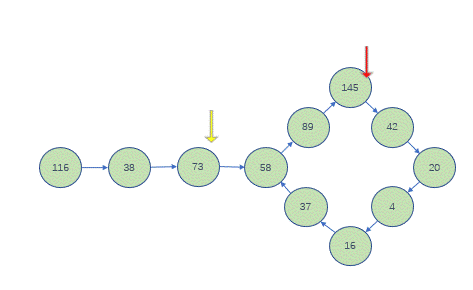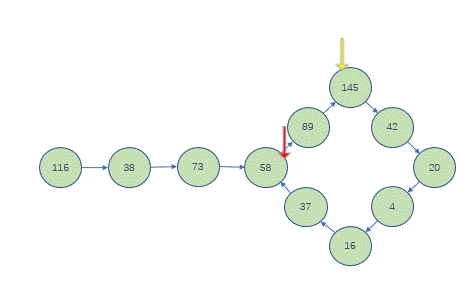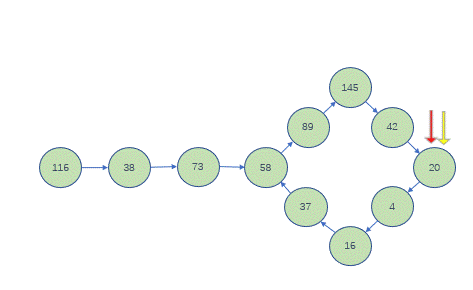

为啥一定不会出现死循环?
因为
int类型最大值为为??2 147 483 647??,所以平方和最大的数是1 999 999 999,平方和为1 + 81*9 = 724。任何数的平方和都在
1到724之间,724次循环之内一定有重复的。
class Solution {
public boolean isHappy(int n) {
// 把转换后的数看作模拟单链表的节点
int slow = n, fast = squareSum(n);
while (fast != slow) {
slow = squareSum(slow);
fast = squareSum(squareSum(fast));
}
// 判断快慢指针的值
// 为1,则为快乐数
return slow==1 ? true : false;
}
private int squareSum(int n){
int squareSum = 0;
while (n != 0) {
squareSum += (n%10) * (n%10);
n /= 10;
}
return squareSum;
}
}
时间复杂度: O ( n ) O(n) O(n),
n为转换的次数。空间复杂度: O ( 1 ) O(1) O(1)
217. 存在重复元素
| 难度 | 简单 | 通过率 | 56.09%(293,091/522,475) |
|---|
题目描述:
给定一个整数数组,判断是否存在重复元素。
如果存在一值在数组中出现至少两次,函数返回
true。如果数组中每个元素都不相同,则返回false。
示例 1:
输入: [1,2,3,1]
输出: true
示例 2:
输入: [1,2,3,4]
输出: false
示例 3:
输入: [1,1,1,3,3,4,3,2,4,2]
输出: true
题解
① Set 不可重复性
class Solution {
/* HashSet.add Set元素不可重复性 */
public boolean containsDuplicate(int[] nums) {
Set set = new HashSet();
for (int num : nums)
if (!set.add(num))
return true;
return false;
}
}
时间复杂度: O ( log ? ? n ) O(\log\,n) O(logn)
空间复杂度: O ( log ? ? n ) O(\log\,n) O(logn)
② 数组排序
class Solution {
/* Arrays.sort */
boolean containsDuplicate_Arrays(int[] nums) {
Arrays.sort(nums);
for (int i = 1; i < nums.length; i++)
if (nums[i] == nums[i-1])
return true;
return false;
}
}
时间复杂度: O ( n ? log ? ? n ) O(n\,\log\,n) O(nlogn) ,即排序的时间复杂度。扫描的时间复杂度 O ( n ) O(n) O(n) 可忽略。
空间复杂度: O ( log ? ? 1 ) O(\log\,1) O(log1) ,没有用到额外空间。如果深究
Arrays.sort(nums)使用了栈空间,那就是 O ( log ? n ) O(\log n) O(logn)。
③ Java Stream的IntStream
- 这是一种很高级的题解,参考“甜姨 Sweetiee”的题解
- Java Stream可以将
int[]转成Set<integer>,为了更简短一些,可以直接利用stream的distinct和count算子。- 如果使用 Python 那更简单:
len(set(nums)) != len(nums)。
- 如果使用 Python 那更简单:
class Solution {
public boolean containsDuplicate(int[] nums) {
// 将 int[] 转成 Set<Integer>
return IntStream.of(nums).distinct().count() != nums.length;
// of(nums):返回其元素是指定值的顺序排序流
// distinct():返回由该流的不同元素组成的流
// count():返回此流中的元素数
}
}
时间复杂度: O ( log ? ? n ) O(\log\,n) O(logn)
空间复杂度: O ( log ? ? n ) O(\log\,n) O(logn)
剑指Offer 3. 数组中重复的数字
| 难度 | 简单 | 通过率 | 67.71%(335,520/495,461) |
|---|
找出数组中重复的数字。
在一个长度为 n 的数组 nums 里的所有数字都在 0~n-1 的范围内。数组中某些数字是重复的,但不知道有几个数字重复了,也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。
示例 1:
输入:
[2, 3, 1, 0, 2, 5, 3]
输出:2 或 3
限制:
- 2 <=
n<= 100000
题解
① 哈希表
- 肯定最先想到的是
哈希表,因为Set的特性:元素不可重复性。
class Solution {
/* Set 元素不可重复性 */
public int findRepeatNumber(int[] nums) {
Set set = new HashSet();
for (int num : nums)
if (!set.add(num))
return num;
return -1;
}
}
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( n ) O(n) O(n)
② 原地算法
- 原地算法可以达到“不适用额外空间”,详细过程见我的手稿:
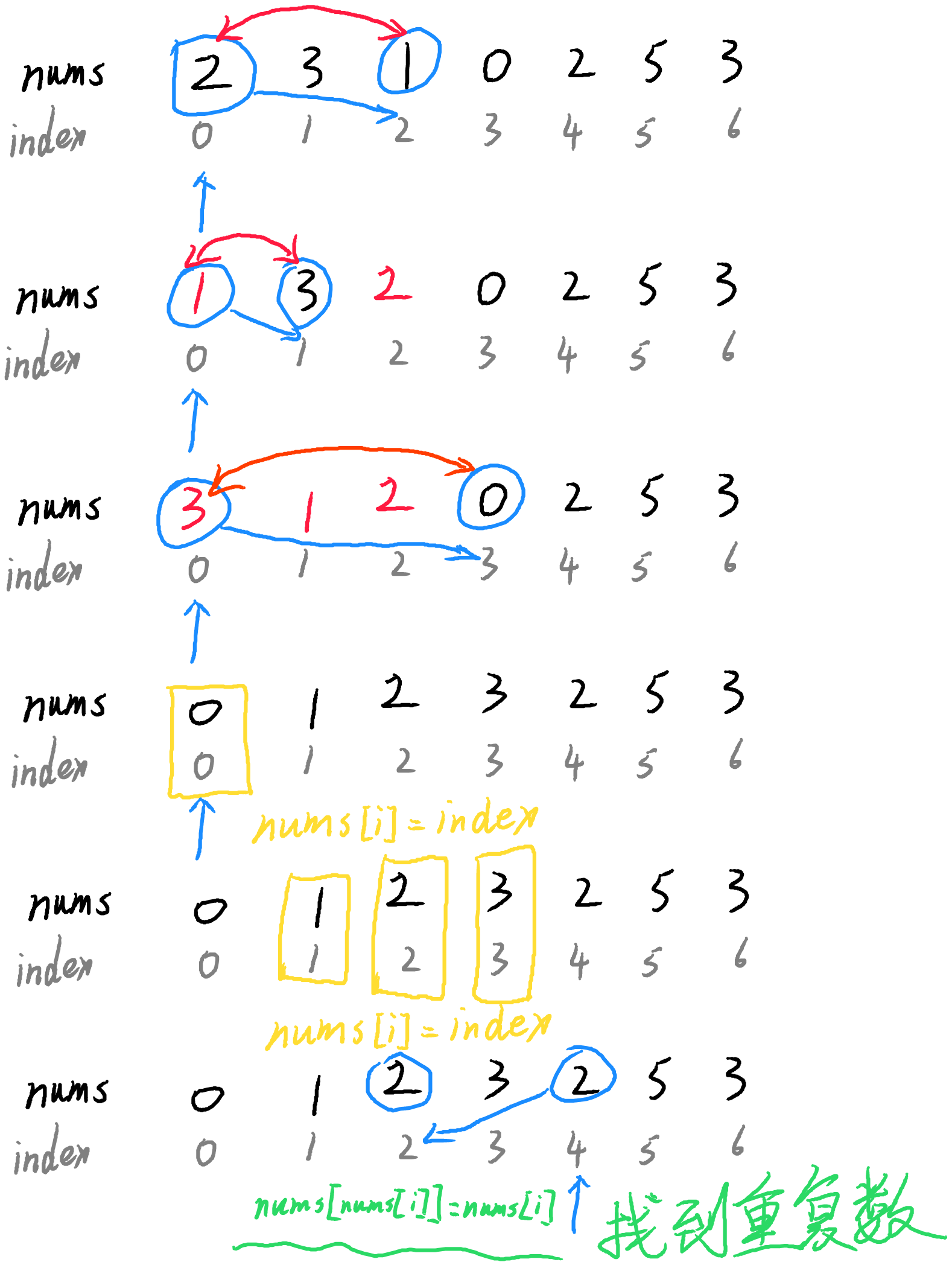
class Solution {
public int findRepeatNumber(int[] nums) {
for (int i = 0; i < nums.length; i++) {
if (nums[i] == i)
continue;
int temp = nums[nums[i]];
nums[nums[i]] = nums[i];
nums[i] = temp;
if (nums[nums[i]] == nums[i])
return nums[i];
}
return -1;
}
}
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( 1 ) O(1) O(1)
③ 数组排序
- 对
nums进行排序后,重复的元素必定 相邻!
class Solution {
public int findRepeatNumber(int[] nums) {
Arrays.sort(nums);
for (int i = 0; i < nums.length-1; i++)
if (nums[i] == nums[i+1])
return nums[i];
return -1;
}
}
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( 1 ) O(1) O(1)
难度:中等
137. 只出现一次的数字 II
| 难度 | 中等 | 通过率 | 71.89%(92,189/128,236) |
|---|
题目描述:
给你一个整数数组
nums,除某个元素仅出现 一次 外,其余每个元素都恰出现 **三次 。**请你找出并返回那个只出现了一次的元素。
示例 1:
输入:nums = [2,2,3,2]
输出:3
示例 2:
输入:nums = [0,1,0,1,0,1,99]
输出:99
提示:
- 1 <=
nums.length<= 3 ? 1 0 4 3 * 10^4 3?104 -
?
2
31
-2^{31}
?231 <=
nums[i]<= 2 31 ? 1 2^{31} - 1 231?1 nums中,除某个元素仅出现 一次 外,其余每个元素都恰出现三次
进阶:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
题解
287. 寻找重复数
| 难度 | 中等 | 通过率 | 66.59%(159,302/239,210) |
|---|
给定一个包含 n + 1 个整数的数组 nums ,其数字都在 1 到 n 之间(包括 1 和 n),可知至少存在一个重复的整数。
假设 nums 只有 一个重复的整数 ,找出 这个重复的数 。
你设计的解决方案必须不修改数组
nums且只用常量级O(1)的额外空间。
示例 1:
输入:nums = [1,3,4,2,2]
输出:2
示例 2:
输入:nums = [3,1,3,4,2]
输出:3
示例 3:
输入:nums = [1,1]
输出:1
示例 4:
输入:nums = [1,1,2]
输出:1
提示:
- 1 <=
n<= 1 0 5 10^5 105 nums.length==n + 1- 1 <=
nums[i]<= n nums中只有一个整数出现两次或多次,其余整数均只出现 一次
进阶:
- 如何证明
nums中至少存在一个重复的数字?- 你可以设计一个线性级时间复杂度
O(n)的解决方案吗?
