这篇文章主要介绍编程中常用到的五大基础算法,下面依次介绍:
一、分治与递归
这里我们引入一个数列,名为斐波那契(Fibonacci)数列。
斐波那契数列,又称黄金分割数列,指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、……在数学上,斐波纳契数列以如下被以递归的方法定义:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N*)在现代物理、准晶体结构、化学等领域,斐波纳契数列都有直接的应用,为此,美国数学会从1963起出版了以《斐波纳契数列季刊》为名的一份数学杂志,用于专门刊载这方面的研究成果。
下面,通过代码来简单理解以下:
如果我们需要求出斐波那契数列的第n项该怎么做呢,这里用到的递归关系在上面斐波那契数列的介绍中已经给出,即F(n)=F(n-1)+F(n-2)(n>=2),F(0)=0,F(1)=1,下面用代码实现:
##递归
def recursion(i:int):
if i==0:
return 0
elif i==1:
return 1
else:
return recursion(i-1)+recursion(i-2)
print(recursion(9))这里求的是斐波那契数列的第9项,输出结果为34。
刚想到前两天更新过二分查找的文章https://blog.csdn.net/zhu_xwt/article/details/118631040?spm=1001.2014.3001.5501,这里用递归实现一下二分查找,以对二分查找做一个复习:
对于这样一个数列,
a=[1,3,4,7,9,14,25,36]
指定一个数x,找出x在数组中的位置,如果x在数组中,返回x对应的元素在数组中的下标,例如,x=7时,需要返回值3;如果x不在数组中,则返回-1。
下面是代码的实现部分:
#用递归的方法实现二分查找
a=[1,3,4,7,9,14,25,36]
x=9
def recursion(a,x,left,right):
if left==right and a[left]!=x:
return -1
else:
while left<=right:
mid=(left+right)//2
if a[mid]==x:
return mid
elif a[mid]>x:
return recursion(a,x,left,mid-1)
else:
return recursion(a,x,mid+1,right)
print(recursion(a,x,0,len(a)))当x=9时,输出为4;
当x=5时,输出为-1;因为5并不在数组中。
二、动态规划
动态规划基本思想和递归算法类似,都是将复杂问题划分为一个个小问题的集合,通过求解前序问题的解得到问题的最终解。其与递归的不同在于,动态规划有重叠子问题:即子问题之间是不独立的,一个子问题在下一阶段决策中可能被多次使用到。例如递归方程F(n)=F(n-1)+F(n-2),如果用递归算法,F(n-1)与F(n-2)的求解过程是相互独立的;如果用动态规划算法,F(n-2)的求解结果会在F(n-1)值的求解中使用到,不需要对F(n-2)再次求解,从而简化了计算过程。
再次引用前面的斐波那契数列,如果用动态规划实现,需要将每一步计算的F(n)的值存放在一个数组中,方便下一步的调用,我对动态规划的理解,可以说,动态规划是一个消耗空间来节省时间的算法,下面是斐波那契数列的动态规划实现:
#动态规划
def dynamic(n):
if n<2:
return n
else:
a=[0,1]
for i in range(2,n+1):
a.append(a[i-1]+a[i-2])
return a[n]
print(dynamic(9))当dynamic()函数括号内的参数为9时,输出结果34。
下面看动态规划的另外一个问题——最大子序列和:
对于数组a=[6,-1,3,-4,-6,9,2,-2,5],找出其中的最大连续子序列和,这个序列中最大连续子序明显为:9,2,-2,5,相加起来为14,即最大子序列和为14,下面是代码的实现部分。
#求最大子序列和
a=[6,-1,3,-4,-6,9,2,-2,5]
sum=0
maxx=0
for i in range(len(a)):
sum=max(sum+a[i],a[i])
if sum>maxx:
maxx=sum
print(maxx)
?ps:这里一开始我设的变量为sum=0,max=0,后来运行时出现错误:
TypeError: 'int' object is not callable
后来发现,是定义的变量max与系统函数max()重名导致。
想了解更多动态规划和递归算法的知识与例子,点击链接https://blog.csdn.net/zw6161080123/article/details/80639932
三、贪心算法
贪心算法是指:在每一步求解的步骤中,它要求“贪婪”的选择最佳操作,并希望通过一系列的最优选择,能够产生一个问题的(全局的)最优解。
贪心算法每一步必须满足一下条件:
1、可行的:即它必须满足问题的约束。
2、局部最优:他是当前步骤中所有可行选择中最佳的局部选择。
3、不可取消:即选择一旦做出,在算法的后面步骤就不可改变了。
下面来看一个典型问题——钱币找零问题
这个问题在我们的日常生活中就更加普遍了。假设1元、2元、5元、10元、20元、50元、100元的纸币分别有c0, c1, c2, c3, c4, c5, c6张。现在要用这些钱来支付K元,至少要用多少张纸币?用贪心算法的思想,很显然,每一步尽可能用面值大的纸币即可。在日常生活中我们自然而然也是这么做的。
下面是代码示例:
#钱币找零问题 #贪心算法
money=[1,5,20,50,100]
count=[3,2,1,2,4]
values=213
def change(money,count,values):
result=[]
dicts=dict(zip(money,count))
info=dict(sorted(dicts.items(),key=lambda x:x[0],reverse=True))#对形成的字典排序
for key,value in info.items():
result.append(min(values//key,value))
values-=result[-1]*key
return result
print(change(money,count,values))?输出结果为?[2, 0, 0, 2, 3]
ps:我的代码水平实在是有限,写这个程序搞得很复杂,这个问题应该是可以更简单一点的
?
四、回溯法
回溯法的基本原理:
在包含问题的所有解的解空间树中,按照深度优先搜索的策略,从根结点出发深度探索解空间树。当探索到某一结点时,要先判断该结点是否包含问题的解,如果包含,就从该结点出发继续探索下去,如果该结点不包含问题的解,则逐层向其祖先结点回溯。(其实回溯法就是对隐式图的深度优先搜索算法)。 若用回溯法求问题的所有解时,要回溯到根,且根结点的所有可行的子树都要已被搜索遍才结束。 而若使用回溯法求任一个解时,只要搜索到问题的一个解就可以结束
听不懂上面这段话没关系,我们下面来看一个代码示例:
背包问题:
有n件物品和一个容量为c的背包。第i件物品的价值是v[i],重量是w[i]。求解将哪些物品装入背包可使价值总和最大。所谓01背包,表示每一个物品只有一个,要么装入,要么不装入。要求求出最大的价值bestprice
下面是代码部分:
#背包问题 #回溯法
i=0
n=5 #物品的个数
c=12 #背包的容量
p=[1,2,3,4,5] #物品的价值
w=[1,3,5,7,2] #物品的重量
cp=0 #总价值
cw=0 #总重量
bestp=0 #物品的最高总价值
bestx=[0,0,0,0,0] #物品的最佳选中情况
x=[0,0,0,0,0] #物品的选中情况
def backtrack(i,cp,cw):#i为回溯深度,cp为当前总价值,cw为当前总重量
global bestp
global bestx
if i>n-1:
if cp>bestp:
bestp=cp
# bestx=x
for j in range(n):
bestx[j]=x[j]
else:
for j in range(0,2):
x[i]=j
if cw+w[i]*x[i]<=c:
cw+=w[i]*x[i]
cp+=p[i]*x[i]
backtrack(i+1,cp,cw)
cw-=w[i]*x[i]
cp-=p[i]*x[i]
backtrack(i,cp,cw)
print(bestp)
print(bestx)
当将各全局变量如代码所示初始化后,输出结果如下:
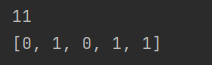
其访问节点的顺序为:

?ps;我要哭了,csdn上传图片为啥总是横着的,将就着看吧。
如果基础不是很好的同学可以去了解一下深度优先搜索https://blog.csdn.net/qq_38442065/article/details/81634282
我搜了一下,感觉网上对深度优先搜索讲的都比较复杂,这个博主讲的还算比较好
五、分支限界法
暂时没学会,学会了过来补充。对不起我太菜了呜呜呜。
?
?
?
?
?