[数据结构与算法]过河卒（动态规划）

洛谷P1002–过河卒（动态规划）

一、题目描述

棋盘上 $A$点有一个过河卒，需要走到目标$B$点。卒行走的规则：可以向下、或者向右。同时在棋盘上$C$点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，$A$ 点 (0,0)(0, 0)(0,0)、$B$点 (n,m)(n, m)(n,m)，同样马的位置坐标是需要给出的。

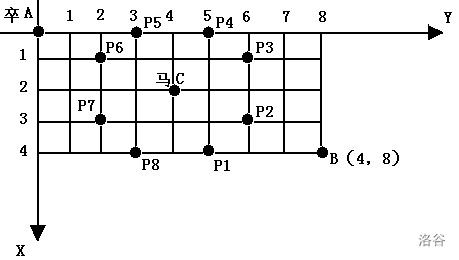
现在要求你计算出卒从 $A$ 点能够到达 $B$ 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。–

• 输入格式

一行四个正整数，分别表示 $B$ 点坐标和马的坐标。

• 输出格式

一个整数，表示所有的路径条数。

• 输入输出样例

输入 #1

6 6 3 3

输出 #1

6

• 说明/提示

对于$100$的数据，$1?m,n?20$,$0?马的坐标?20$.

二、解析

• 分析棋盘上到每个点的路径数目，如下图所示：

  

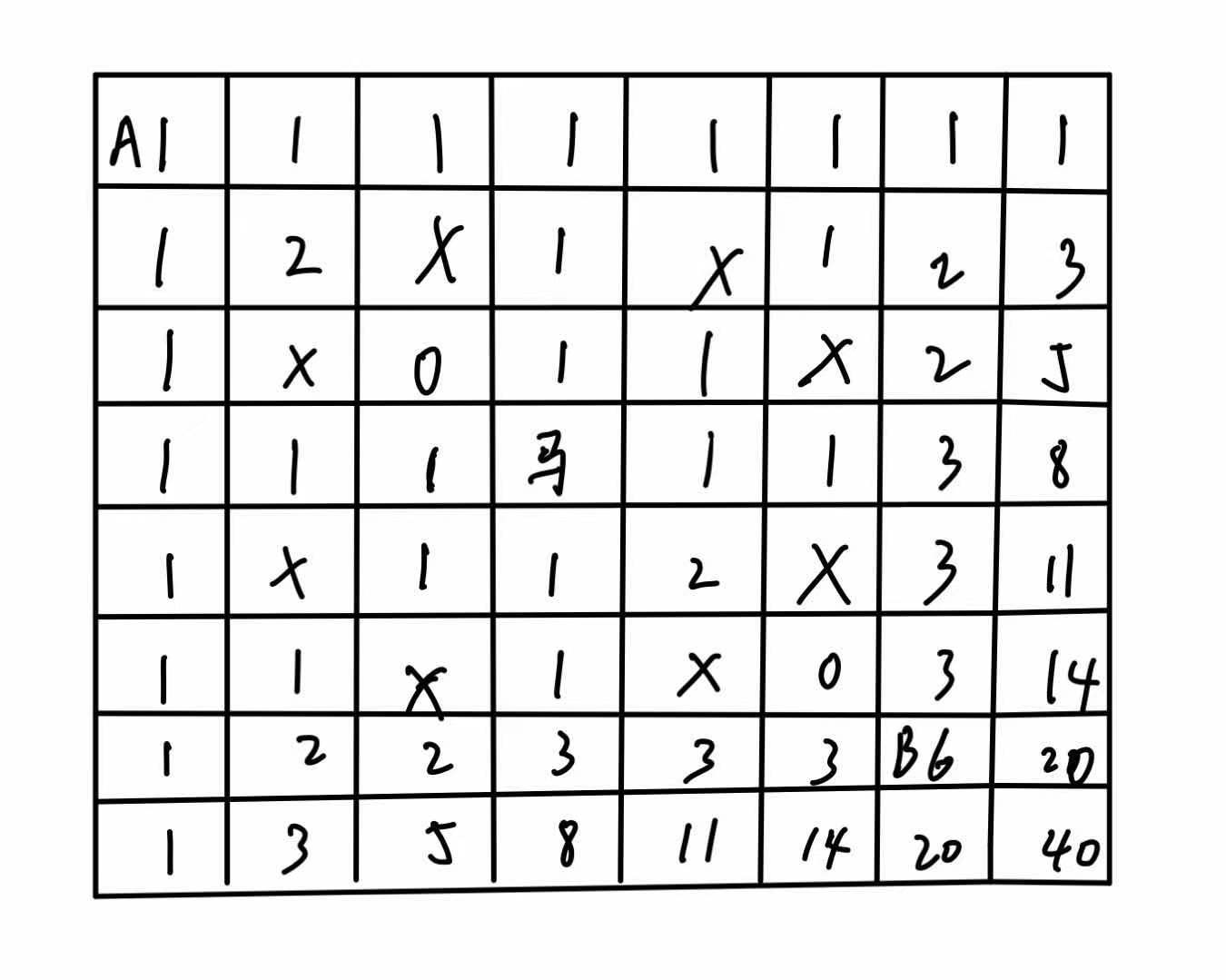
• 据此，我们可以得出一个迭代式的(x,y)=(x-1,y)+(x,y-1).

• 动态规划检查是否越界时我们可以将整个图向右下方移动一个单位，空出一行一列便于越界检查。

• 象棋中马的走法是固定的(即马走日字)，我们可以用一个数组记录马的八种走法（主要越界检查）。将马可以走的位置设为零。

• 初始化迭代时设(1,0)处=1，通过使用迭代式算出每一个点从A点可以到达的路径数，（也可以设(0,1)处=1，道理是相同的）.

• 迭代完成后b点坐标处得出的路径数即为A到B得路径数。

三、代码实现

#include<iostream>
#include<algorithm>
using namespace std;
long long dp[30][30];
int m_x[8]={-2,-2,-1,-1,1,1,2,2},m_y[8]={1,-1,2,-2,2,-2,1,-1};//马跳的坐标变化

int main(){
    int n,m,x,y;
    cin>>n>>m>>x>>y;
    n+=1;m+=1;x+=1;y+=1;//整体空出一行一列，便于边界检查
    for(int i=0;i<8;i++){
        if(x+m_x[i]>=1&&x+m_x[i]<=n&&y+m_y[i]>=1&&y+m_y[i]<=m)
            dp[x+m_x[i]][y+m_y[i]]=-1;
    }
    dp[1][0]=1;
    dp[x][y]=-1;//马所在的点也不能走
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(dp[i][j]==-1)
                dp[i][j]=0;
            else{
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }
    }

    cout<<dp[n][m];

    system("pause");
    return 0;
}