题解篇(牛客练习赛86)
牛客练习赛86,难度适中,前三题分别为博弈、构造、贪心DP,第三题较难,比赛中没有写出来, 但好在前两题手速比较快,所以这场比赛也没掉分;
A、 取因数
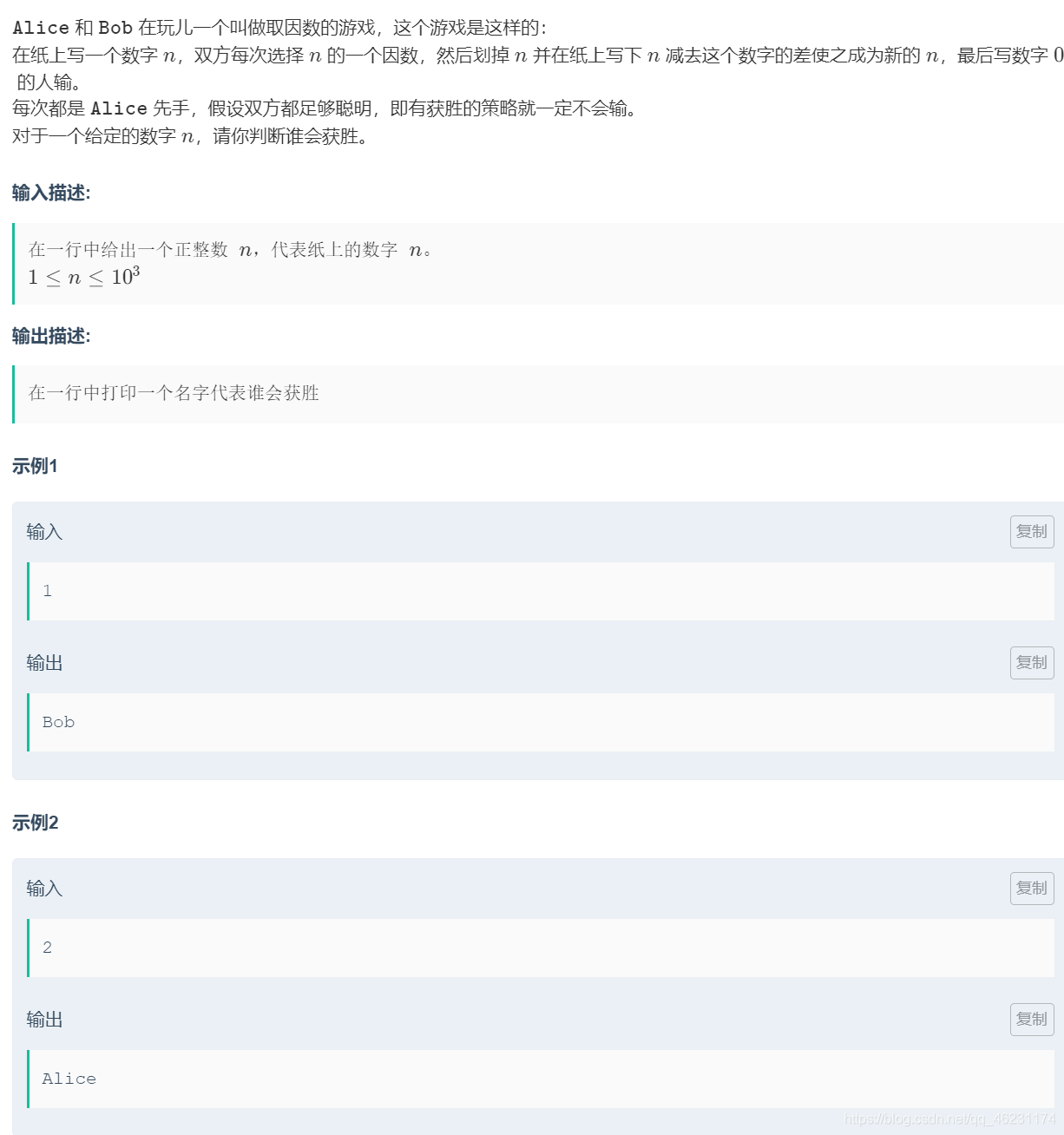
题意:A和B玩数字游戏,开始给出一个数字n,A先减去这个数字的一个因数x,将数字n变为n-x,而后B同样找出一个因数,让变换后的数字减去这个因数,以此类推,最后谁先把数字变成0,谁就输了。
题目要求A和B都用最优策略解决,很明显的博弈题目;
解题思路:将数字n分为两种情况, 奇数和偶数;
1、对于每一个数字n,若n为奇数,则它的因数只有奇数(因为偶乘偶得偶,偶乘奇得偶,只有奇乘奇得奇),则奇数变换后一定是偶数;
2、对于每一个数字n,若n为偶数,则它的因数一定有一个奇数1,则每一个偶数一定能变成奇数;
所以对于每一个数字n来回变化,每人都使用最优策略,则一定会有一次变为2,此时因数只有1,则2在谁手上,谁就能赢,化零为整,则n为偶数先手必胜,n为奇数后手必胜
#include <iostream>
#include <algorithm>
#include <map>
#include <cstring>
#include <queue>
#include <cmath>
#include <vector>
#include <unordered_map>
using namespace std;
typedef long long ll;
typedef long double ld;
const int N = 100005;
const int inf = 0x3f3f3f3f;
const int mod = 1e9+7;
int main()
{
ios::sync_with_stdio(false), cout.tie(0), cin.tie(0);
int n;
cin>>n;
if(n%2 == 0)cout<<"Alice"<<endl;
else cout<<"Bob"<<endl;
return 0;
}
B、A+B
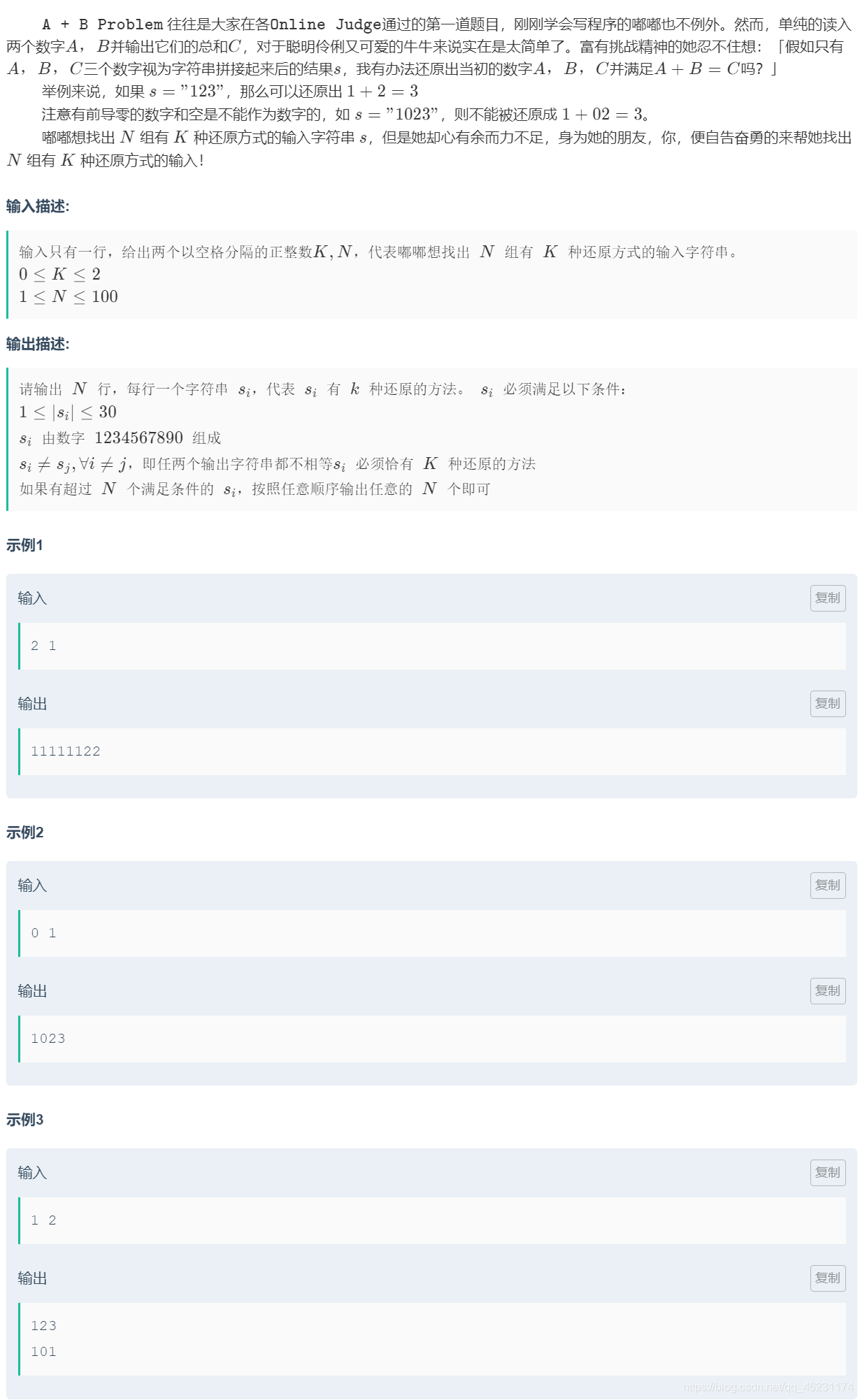
题意:构造一个字符串s(仅包含数字),使得s能按顺序分解成三个字符串a、b、c(a+b+c = s),他们转换为数字的情况下满足数学计算a+b = c,一个字符串s有k种分割方式;给出n和k;构造出n个字符串,每个字符串有k种分割方式。
解题思路:k的取值范围是0~2,由此可以对不同的k分类讨论:
1、当k等于0时比较简单,可以构造出字符串x0yz,因为不能含有前导零,则只能分解成x0,y和z,此时无论x,y,z为何数,皆满足k为0;
2、当k等于1时,可以构造出形如xyzw0xyzw的模式此时只包含算式xyzw+0 = xyzw;
3、当k等于2时,可以构造出形如11111122 这类的111+11 = 122,11+111 = 122,这类的x+y = z,y+x = z;
此时可以令x不变y公差为一递增,达到上限时将x赋值为222再以相同的方式递增;
int main()
{
// ios::sync_with_stdio(false), cout.tie(0), cin.tie(0);
int n, k;
cin>>k>>n;
if(k == 0){
int x = 1;
int y = 23;
int t = 1;
while(n--){
printf("%d0%d\n", x, y);
y++;
if(y>=100&&t){
t = 0;
x = 2;
y = 34;
}
}
}
else if(k == 1){//这里和上面说的构造方法不一样,但是上面的k = 1的构造方法更加简单
int x = 1, y = 2;
int t = 1;
while(n--){
printf("%d%d%d\n", x, y, x+y);
y++;
if(y>9){
y = 1;
x++;
if(x>10&&t){
x = 101;
t = 0;
}
else if(x>100&&!t){
x = 1001;
}
}
}
}
else if(k == 2){
int x = 111;
int y = 11;
int t = 1;
while(n--){
printf("%d%d%d\n", x, y, x+y);
y++;
if(y>=100&&t){
t = 0;
x = 222;
y = 11;
}
}
}
return 0;
}
C、取钱
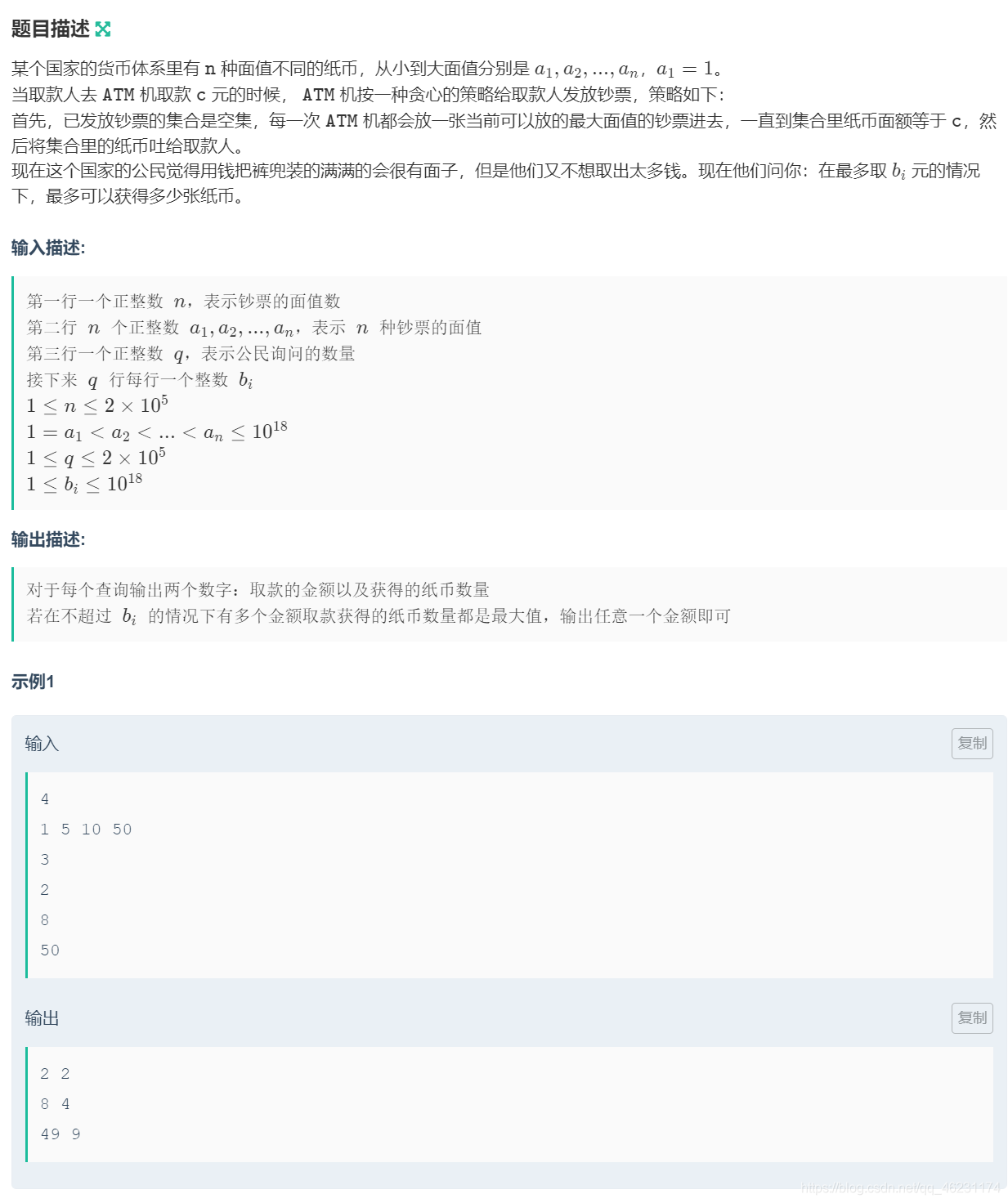
题意:题意不难理解,看题目就行;
解题思路:首先,数据范围较大,但凑取纸币需要找到当前纸币集合(a)内最大的比b小的数,由此先想到二分,那么对于每个b怎样才能使得所取的面额x得到的纸币数量最多;
首先预处理dp数组,dp[i]表示最多取面值为a[i]时最多能取多少张(i>=2,因为a1恒为1),设此时面额为x;则x不可能取a[i](取a[i]就直接为一张),则对a[i]-1操作 找到a[i]-1最多能凑成的多少张,将其减少一张a[i-1],将其替换为dp[i-1],然后比较一下哪个比较大;
#include <iostream>
#include <algorithm>
#include <map>
#include <cstring>
#include <queue>
#include <cmath>
#include <vector>
#include <unordered_map>
using namespace std;
typedef long long ll;
typedef long double ld;
const int N = 2e5+5;
const int inf = 0x3f3f3f3f;
const int mod = 1e9+7;
ll a[N];
pair<ll, ll> dp[N];
ll n;
pair<ll, ll> lq(ll x){
if(x == 0) return {0,0};
ll res = upper_bound(a+1, a+n+1, x) - a;
res--;//最大的小于x的数
ll num = x%a[res];
ll u = x/a[res];
ll ans = u;
ll cnt = u*a[res];
pair<ll, ll> t = lq(num);
if(dp[res].first +u-1 >= ans+t.first){
ans = dp[res].first+u-1;
cnt = dp[res].second+(u-1)*a[res];
}
else{
ans = ans+t.first;
cnt = cnt+t.second;
}
return {ans, cnt};
}
int main()
{
// ios::sync_with_stdio(false), cout.tie(0), cin.tie(0);
scanf("%lld", &n);
for(int i = 1; i<=n; i++)scanf("%lld", &a[i]);
dp[1].first = 0, dp[1].second = 0;
for(int i = 2; i<=n;i++){
ll x = a[i]-1;
pair<ll, ll>t = lq(x);
dp[i] .first = t.first;
dp[i].second = t.second;
}
// for(int i = 1; i<=n; i++) cout<<dp[i].first<<' '<<dp[i].second<<endl;
int q;
scanf("%d", &q);
while(q--){
ll x;
scanf("%lld", &x);
pair<ll, ll>t = lq(x);
printf("%lld %lld\n", t.second, t.first);
}
return 0;
}