算法是作用于具体数据结构之上的,深度优先搜索算法和广度优先搜索算法都是基于“图”这种数据结构的。这是因为,图这种数据结构的表达能力很强,大部分涉及搜索的场景都可以抽象成“图”。
图上的搜索算法,最直接的理解就是,在图中找出从一个顶点出发,到另一个顶点的路径。为了搞清楚图的搜索算法,必须先把图的存储方式理解透彻。
图的存储
图有多种存储方法,最常用的两种分别是:邻接矩阵和出边数组。
邻接矩阵的存储方式如下图所示,底层依赖一个二维数组。
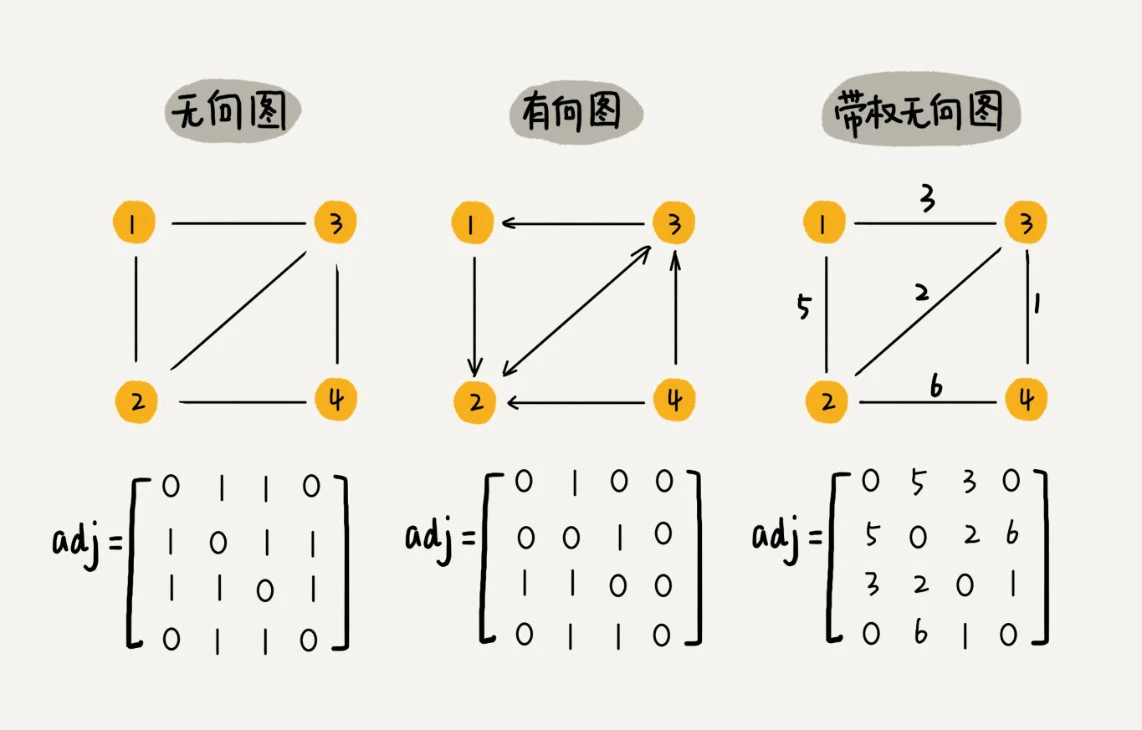
对于无向图来说,如果顶点i与顶点j之间有边,我们就将A[i][j]和 A[j][i]标记1;对于有向图来说,如果顶点i到顶点j之间,有一条箭头从顶点i指向顶点j的边,那我们就将A[i][j]标记为1。同理,如果有一条箭头从顶点j指向顶点i的边,我们就将A[j][i]标记为1。对于带权图,数组中就存储相应的权重。
用邻接矩阵来表示一个图,虽然简单、直观,但是比较浪费存储空间。对于无向图来说,如果A[i][j]等于1,那A[j][i]也肯定等于1。实际上,我们只需要存储一个就可以了。也就是说,无向图的二维数组中,如果我们将其用对角线划分为上下两部分,那我们只需要利用上面或者下面这样一半的空间就足够了,另外一半白白浪费掉了。
针对上面邻接矩阵比较浪费内存空间的问题,出边数组可以避免空间浪费。如下图所示,每个顶点对应一条链表,链表中存储的是与这个顶点相连接的其他顶点。

例如上图中,我们要确定,是否存在一条从顶点2到顶点4的边,那我们就要遍历顶点2的所有出边,看出边是否能到达顶点4。所以,比起邻接矩阵的存储方式,在出边数组中查询两个顶点之间的关系就没那么高效了。
//无向图
public class UndirectedGraph {
/**
* 顶点的个数
*/
private int v;
/**
* 邻接表(出边数组)
*/
private ArrayList<Integer>[] edges;
public UndirectedGraph(int v) {
this.v = v;
edges = new ArrayList[v];
for (int i = 0; i < v; ++i) {
edges[i] = new ArrayList<>();
}
}
/**
* 对于无向图,其实就是点s到点t的两条边
* 用两条有向边代表无向图中的一条边
*/
public void addEdge(int s, int t) {
edges[s].add(t);
edges[t].add(s);
}
}
深度优先搜索(DFS)
深度优先搜索用的是一种比较著名的算法思想,回溯思想。这种思想解决问题的过程,非常适合用递归来实现。例如下图中演示了用深度优先搜索的思想寻找一条从点s到点c的路径的方法。从图中我们可以看出,深度优先搜索找出来的路径,并不是点s到点c的最短路径。
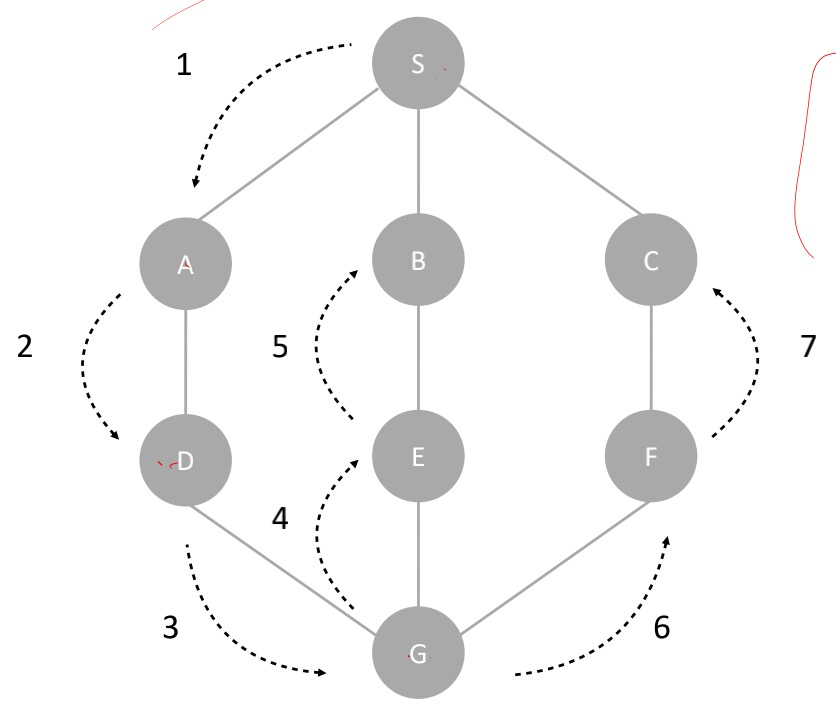
我把上面的过程用递归的形式写下来如下。深度优先搜索代码里,有个比较特殊的全局变量found,它的作用是,当我们已经找到终止点之后,我们就不再递归地继续查找了。
//全局变量或者类成员变量
boolean found = false;
private int v;
private ArrayList<Integer>[] edges;
public void existPath(int start, int t) {
boolean[] visited = new boolean[v];
recurDfs(start, t, visited);
}
private void recurDfs(int current, int t, boolean[] visited) {
if (found == true) {
return;
}
visited[current] = true;
if (current == t) {
found = true;
return;
}
for (int i = 0; i < edges[current].size(); ++i) {
int q = edges[current].get(i);
if (!visited[q]) {
recurDfs(q, t, visited);
}
}
}
理解了深度优先搜索算法之后,深度优先搜索的时间、空间复杂度是多少呢?从示意图可以看出,每条边最多会被访问两次,一次是遍历,一次是回退。所以,图上的深度优先搜索算法的时间复杂度是O(E),E表示边数。深度优先搜索算法的消耗内存主要是visited、数组和递归调用栈。visited数组的大小跟顶点的个数V成正比,递归调用栈的最大深度不会超过顶点的个数,所以总的空间复杂度就是O(V)。
广度优先搜索(BFS)
广度优先搜索直观地讲,就是一种“地毯式”层层推进的搜索策略,即先查找离起始顶点最近的,然后是次近的,依次往外搜索。理解起来并不难,示意图如下。

尽管广度优先搜索的原理挺简单,但代码实现还是稍微有点复杂度。实际上,这样得到的一条路径就是从起始点到指定点的最短路径。
private boolean existPathBfs(int current, int t) {
if (current == t) {
return true;
}
visited[current] = true;
Queue<Integer> queue = new ArrayDeque<>();
queue.add(current);
while (!queue.isEmpty()) {
int point = queue.poll();
for (int i = 0; i < edges[point].size(); ++i) {
int q = edges[point].get(i);
if (!visited[q]) {
if (q == t) {
return true;
}
queue.add(q);
visited[q] = true;
}
}
}
return false;
}
BFS代码中的queue是一个队列,用来存储已经被访问、但相连的顶点还没有被访问的顶点。因为广度优先搜索是逐层访问的,也就是说,我们只有把第k层的顶点都访问完成之后,才能访问第k+1层的顶点。当我们访问到第k层的顶点的时候,我们需要把第k层的顶点记录下来,稍后才能通过第k层的顶点来找第k+1层的顶点。所以,我们用这个队列来实现记录的功能。
广度优先搜索的时间、空间复杂度是多少呢?最坏情况下,终止顶点t离起始顶点s很远,需要遍历完整个图才能找到。这个时候,每个顶点都要进出一遍队列,每个边也都会被访问一次,所以,广度优先搜索的时间复杂度是 O(V+E),其中,V表示顶点的个数,E表示边的个数。当然,对于一个连通图来说,也就是说一个图中的所有顶点都是连通的,E肯定要大于等于V-1,所以,广度优先搜索的时间复杂度也可以简写为O(E)。空间消耗主要在几个辅助变量visited数组、queue队列上。这三个存储空间的大小都不会超过顶点的个数,所以空间复杂度是O(V)。
DFS与BFS的实际应用
样题一:岛屿的数量
给你一个由’1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。此外,你可以假设该网格的四条边均被水包围。

DFS的思路:将二维网格看成一个无向图,竖直或水平相邻的点’1’之间有边相连。为了求出岛屿的数量,我们可以扫描整个二维网格。如果一个位置为’1’,则以其为起始节点开始进行深度优先搜索。在深度优先搜索的过程中,每个搜索到的’1’都会被重新标记。
最终岛屿的数量就是我们进行深度优先搜索的次数。
class Solution {
//垂直水平四个方向组成的方向数组
private int[] dx = {-1,0,1,0};
private int[] dy = {0,1,0,-1};
private boolean[][] visited;
public int numIslands(char[][] grid) {
visited = new boolean[grid.length][grid[0].length];
int ans = 0;
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
if (grid[i][j] == '1' && !visited[i][j]) {
//以grid[i][j]这个点为起点,作深度优先遍历
dfs(grid, i, j);
//遍历的次数就是图中陆地独立成片的块数
ans++;
}
}
}
return ans;
}
//从点(x,y)出发,深度优先遍历
private void dfs(char[][] grid, int x, int y) {
//标记当前点grid[x][y]已经访问过了
visited[x][y] = true;
//然后遍历grid[x][y]点的所有出边,这里就是上下左右4个
for (int i = 0; i < 4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
//判断坐标合法时,才继续遍历
if(nx < 0 || nx >= grid.length || ny < 0 || ny >= grid[0].length) {
continue;
}
//只遍历没访问过且为陆地的点
if (grid[nx][ny] == '1' && !visited[nx][ny]) {
dfs(grid, nx, ny);
}
}
}
}
同样地,我们也可以使用广度优先搜索代替深度优先搜索。
BFS的思路:为了求出岛屿的数量,我们可以扫描整个二维网格。如果一个位置为‘1’,则将其加入队列,开始进行广度优先搜索。在广度优先搜索的过程中,从原点出发能到达的每个点‘1’都会被重新标记。直到队列为空,搜索结束。
最终岛屿的数量就是我们进行广度优先搜索的次数。
class Solution {
//垂直水平四个方向组成的方向数组
private int[] dx = {-1,0,1,0};
private int[] dy = {0,1,0,-1};
private boolean[][] visited;
public int numIslands(char[][] grid) {
visited = new boolean[grid.length][grid[0].length];
int ans = 0;
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
if (grid[i][j] == '1' && !visited[i][j]) {
//以grid[i][j]这个点为起点,作广度优先遍历
bfs(grid, i, j);
ans++;
}
}
}
return ans;
}
//从点(x,y)出发,广度优先遍历
private void bfs(char[][] grid, int x, int y) {
//标记点(x,y)为已经访问过了
visited[x][y] = true;
Queue<Pair> queue = new ArrayDeque<>();
queue.add(new Pair(x, y));
while (!queue.isEmpty()) {
Pair pair = queue.poll();
//然后遍历grid[x][y]点的所有出边,这里就是上下左右4个
for (int i = 0; i < 4; i++) {
int nx = pair.row + dx[i];
int ny = pair.column + dy[i];
//判断坐标合法时,才继续遍历
if(nx < 0 || nx >= grid.length || ny < 0 || ny >= grid[0].length) {
continue;
}
//只遍历没访问过且为陆地的点
if (grid[nx][ny] == '1' && !visited[nx][ny]) {
queue.add(new Pair(nx, ny));
//入队时标记visited数组
visited[nx][ny] = true;
}
}
}
}
class Pair {
int row;
int column;
public Pair(int row, int column) {
this.row = row;
this.column = column;
}
}
}
样题二:被包围的区域
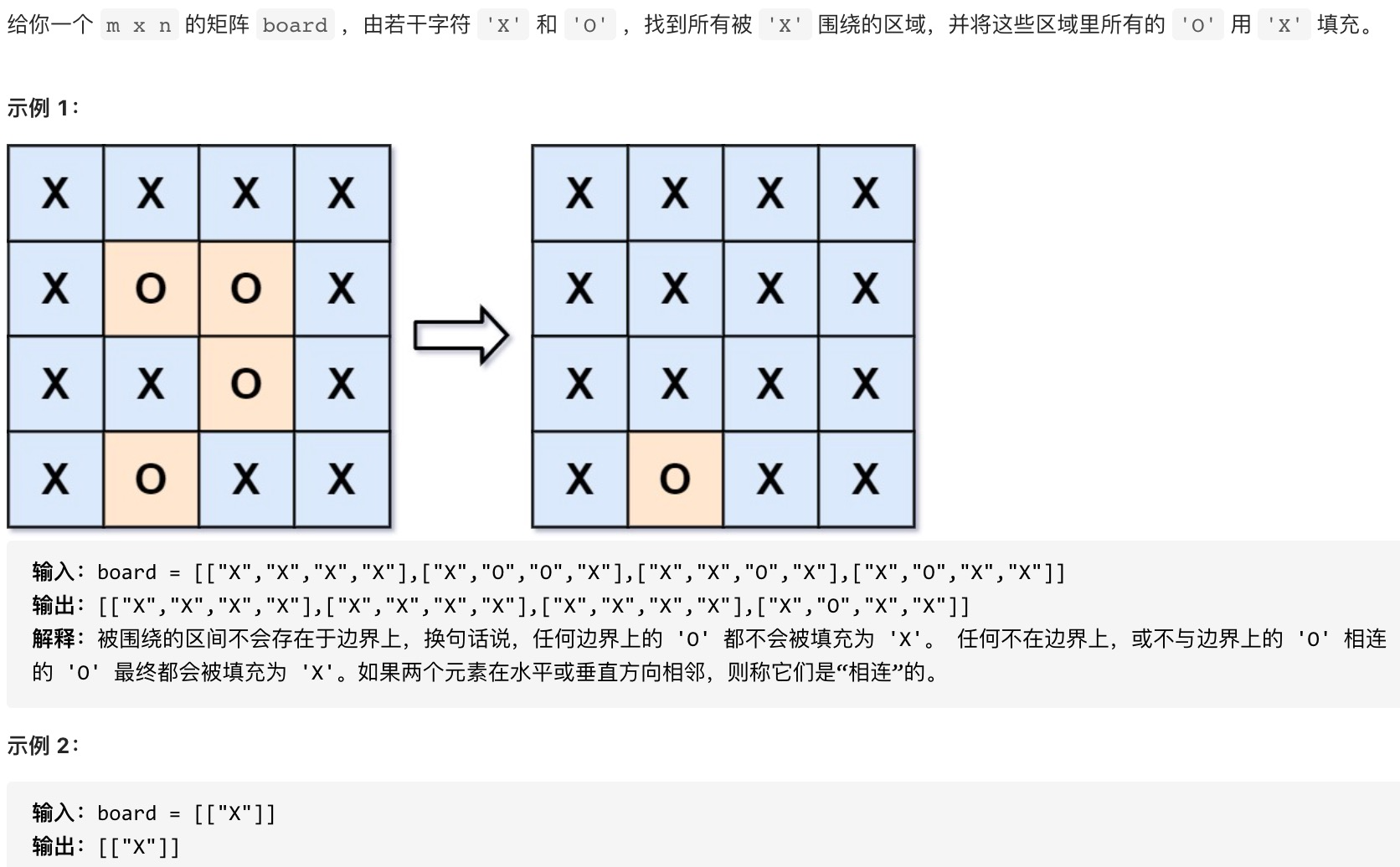
注意关键解释:被围绕的区域不会存在于边界上,换句话说,任何边界上的 ‘O’ 都不会被填充为 ‘X’。 任何不在边界上,或不与边界上的 ‘O’ 相连的 ‘O’ 最终都会被填充为 ‘X’。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。
问题可以转化为:从边界上的‘O’出发所有能被访问到的‘O’都不能被填充为’X’,剩下的‘O’可以被填充为’X’,这是一个搜索问题。
思路:将所有存在于边界上的点’O’都打上标记,例如标记为’#’,然后从这些点出发作搜索,所有能到达的点’O’也打上标记’#’,最后将矩阵中所有标记为’#‘的点都填充为’O’,所有为’O’的点都填充为’X’。
DFS思路下的代码。
class Solution {
private int[] dx = {-1,0,1,0};
private int[] dy = {0,1,0,-1};
private boolean[][] visited;
//寻找和边界连通的O,如果这个O与边界连通,那么不能替换,否则要替换
public void solve(char[][] board) {
visited = new boolean[board.length][board[0].length];
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[0].length; j++) {
if (board[i][j] == 'X') {
continue;
}
//判断点是否在边界上,如果在边界上并且是O,并且没访问过,就访问一次
boolean isEdge = (i == 0 || j == 0 || i == board.length - 1 || j == board[0].length - 1);
if (isEdge && board[i][j] == 'O') {
dfs(board, i, j);
}
}
}
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[0].length; j++) {
if (board[i][j] == 'O') {
board[i][j] = 'X';
} else if (board[i][j] == '#') {
board[i][j] = 'O';
continue;
}
}
}
}
//从点(x,y)出发作深度优先遍历,访问从点(x,y)所能到达的所有点
private void dfs(char[][] board, int x, int y) {
if (board[x][y] == '#') {
return;
}
visited[x][y] = true;
board[x][y] = '#';
//然后遍历board[x][y]的所有点,这里就是上下左右4个
for (int i = 0; i < 4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
//判断坐标合法时,才继续遍历
if(nx < 0 || nx >= board.length || ny < 0 || ny >= board[0].length) {
continue;
}
//只遍历没访问过且为'O'的点
if (board[nx][ny] == 'O' && !visited[nx][ny]) {
dfs(board, nx, ny);
}
}
}
}
BFS思路下的代码。
class Solution {
private int[] dx = {-1,0,1,0};
private int[] dy = {0,1,0,-1};
private boolean[][] visited;
//寻找和边界连通的O,如果这个O与边界连通,那么不能替换,否则要替换
public void solve(char[][] board) {
visited = new boolean[board.length][board[0].length];
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[0].length; j++) {
if (board[i][j] == 'X') {
continue;
}
//判断点是否在边界上,如果在边界上并且是'O',并且没访问过,就访问一次
boolean isEdge = (i == 0 || j == 0 || i == board.length - 1 || j == board[0].length - 1);
if (isEdge && board[i][j] == 'O') {
bfs(board, i, j);
}
}
}
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[0].length; j++) {
if (board[i][j] == 'O') {
board[i][j] = 'X';
} else if (board[i][j] == '#') {
board[i][j] = 'O';
continue;
}
}
}
}
//从点(x,y)出发作深度优先遍历,访问从点(x,y)所能到达的所有点
private void bfs(char[][] board, int x, int y) {
visited[x][y] = true;
board[x][y] = '#';
Queue<Pair> queue = new ArrayDeque<>();
queue.add(new Pair(x, y));
while (!queue.isEmpty()) {
Pair pair = queue.poll();
//然后遍历board[x][y]的所有点,这里就是上下左右4个
for (int i = 0; i < 4; i++) {
int nx = pair.row + dx[i];
int ny = pair.column + dy[i];
//判断坐标合法时,才继续遍历
if(nx < 0 || nx >= board.length || ny < 0 || ny >= board[0].length) {
continue;
}
//只遍历没访问过且为'O'的点
if (board[nx][ny] == 'O' && !visited[nx][ny]) {
queue.add(new Pair(nx, ny));
visited[nx][ny] = true;
board[nx][ny] = '#';
}
}
}
}
class Pair {
int row;
int column;
public Pair(int row, int column) {
this.row = row;
this.column = column;
}
}
}
小结
广度优先搜索,通俗的理解就是,地毯式层层推进,从起始顶点开始,依次往外遍历,遍历得到的路径就是,起始顶点到终止顶点的最短路径。广度优先搜索需要借助队列来实现。深度优先搜索用的是回溯思想,非常适合用递归实现。二者是图上的两种最常用、最基本的搜索算法,比起其他高级的搜索算法,比如A*、IDA*等,要简单粗暴,没有什么优化,所以,也被叫作暴力搜索算法。所以,这两种搜索算法仅适用于状态空间不大,也就是说图不大的搜索。