[数据结构与算法]二叉树遍历

二叉树(binary tree)是结点的有限集合，这个集合或者空，或者由一个根及两个互不相交的称为这个根的左子树或右子树构成.
从定义可以看出，二叉树包括：1.空树 2.只有一个根节点 3.只有左子树 4.只有右子树 5.左右子树都存在 有且仅有这5中表现形式
二叉树的特点：
性质1：在二叉树的第i层上至多有2^(i-1)个节点(i >= 1)
性质2：深度为k的二叉树至多有2^k-1个节点(k >=1)
性质3：对于任意一棵二叉树T而言，其叶子节点数目为N0,度为2的节点数目为N2，则有N0 = N2 + 1。
性质4：具有n个节点的完全二叉树的深度 。

二叉树的遍历分为三种：前序遍历 中序遍历 后序遍历
前序遍历：按照“根左右”,先遍历根节点，再遍历左子树 ，再遍历右子树
中序遍历：按照“左根右“,先遍历左子树，再遍历根节点，最后遍历右子树
后续遍历：按照“左右根”，先遍历左子树，再遍历右子树，最后遍历根节点
其中前，后，中指的是每次遍历时候的根节点被遍历的顺序

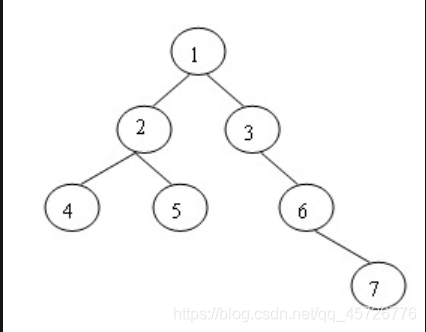
前序遍历：1 2 4 5 3 6 7
中序遍历：4 2 5 1 3 6 7
后序遍历：4 5 2 7 6 3 1

实例：
遍历下列二叉树

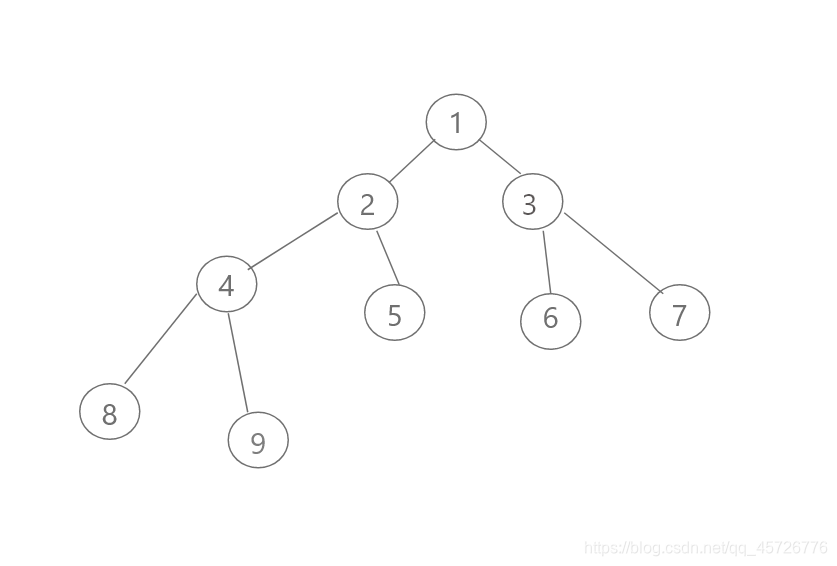
//定义一个节点
class TreeNode {
    int data;
    TreeNode left;
    TreeNode right;
    public TreeNode(int date) {
        left = null;
        right = null;
        this.data= data;
    }
}

//建立一颗二叉树
    public List<TreeNode> createTree(){
        int[] array = {1,2,3,4,5,6,7,8,9};
        List<TreeNode> nodeList = new ArrayList<>();
        for (int nodeIndex = 0; nodeIndex < array.length;nodeIndex++){
            nodeList.add(new TreeNode(array[nodeIndex]));
        }
        //对LastParentIndex-1个父节点按照父节点和子节点的关系建立二叉树
        for (int parentIndex = 0; parentIndex < array.length/2-1;parentIndex++){
            //左孩子
            nodeList.get(parentIndex).left =  nodeList.get(parentIndex * 2 +1);
            //右孩子
            nodeList.get(parentIndex).right =  nodeList.get(parentIndex * 2 +2);
        }
        //最后一个父节点，可能存在没有右孩子的情况，所以拿出来单独处理
        int lastParentIndex = array.length/2-1;
        //左孩子
        nodeList.get(lastParentIndex).left =  nodeList.get(lastParentIndex * 2 + 1);
        //右孩子，如果长度为奇数则建立右孩子
        if(array.length % 2 == 1){
            nodeList.get(lastParentIndex).right = nodeList.get(lastParentIndex * 2 + 2);
        }
        return nodeList;
    }

//前序遍历（根左右）,递归方式
    public static void preOderTraverse(TreeNode node)
    {
        if(node == null)
            return;
        System.out.print(node.data+ " ");
        preOderTraverse(node.left);
        preOderTraverse(node.right);
    }
    //结果应该为1-2-4-8-9-5-3-6-7

//中序遍历(左根右),递归方式
    public static void inOrderTraverse(TreeNode node){
        if(node == null)
            return;
        inOrderTraverse(node.left);
        System.out.print(node.data+" ");
        inOrderTraverse(node.right);
    }//结果应该为8-4-9-2-5-1-6-3-7

//后序遍历(左右根),递归方式
    public static void postOrdeTraverse(TreeNode node){
        if(node == null)
            return;
        postOrdeTraverse(node.left);
        postOrdeTraverse(node.right);
        System.out.print(node.data+" ");
      }//结果应该为8-9-4-5-2-6-7-3-1