题目:设一颗二叉树中各节点的值互不相同,其先序遍历序列和中序遍历序列分别存于两个一维数组A、B中,试编写算法建立该二叉树的二叉链表
递归方式
这道题答案是使用递归创建的,思路是把中序序列看做一个个的块,每个块代表一颗子树中各结点的集合(一整块代表整棵树的左右结点),根据先序序列得到这颗子树的根结点,不断缩小块的大小,直到一个块只剩下一个结点。
递归函数有四个主要参数:块在先序序列和后序序列中的位置
下面的代码是答案给出的代码:
void Creat(ElemType A[], ElemType B[], int l1, int h1, int l2, int h2)
{
//l1, h1为先序的第一和最后一个结点的下标,l2, h2为中序的第一个和最后一个结点的下标
//初始调用时,l1 = l2 = 1, h1 = h2 = n
root = (BiNode*)malloc(sizeof(BiNode)); //创建根结点
root->data = A[l1]; //根结点
for(int i = l2; B[i] != root->data; i++); //找到中序序列中根结点位置
int llen = i - l2;
int rlen = h2 - i; //左右子树长度
if(llen) //递归创建左子树
root->lchild = Creat(A, B, l1 + 1, l1 + llen, l2, l2 + llen - 1);
else
root->lchild = NULL;
if(rlen) //递归创建右子树
root->rchild = Creat(A, B, h1 - rlen + 1, h1, h2 - rlen + 1, h2);
else
root->rchild = NULL;
return root; //返回根结点指针
}
非递归方式
答案只给出了递归方式的创建方法,那么该如何非递归方式创建呢?
考虑到先序序列和后序序列分别对应着入栈序列和出栈序列,可以从出入栈的角度入手。
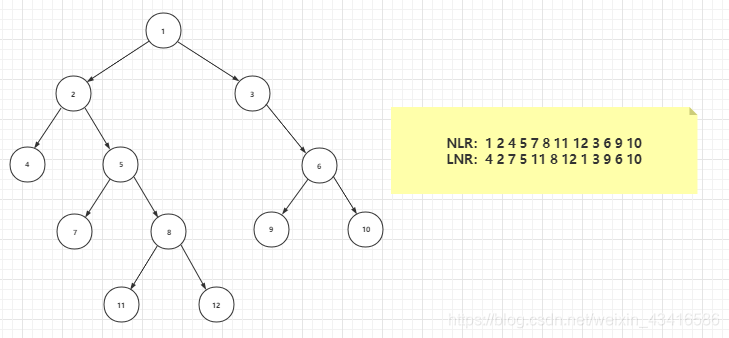
分析两个序列,可以看到:每次入栈时,都是将入栈结点作为左孩子的,而出栈一次,就把当前结点改为其父节点,下次入栈,将入栈元素作为右孩子
因此可以得到创建树的步骤为:
(使用一个结点类型的二重指针p作为当前处理结点)
- 创建一个结点(*p),结点数据赋值为A[i]
将处理结点p变为这个结点的左孩子 : p = &((*p)->left) - 比较栈顶元素与B[j]:
如果相等,说明要出栈,出栈并且将处理结点p变为出栈结点的右孩子:Pop(&m), p = &(m->right), j++,继续2,直到不相等为止
如果不相等,转1(直到j的值等于结点数量退出循环)
根据步骤得到下面代码:
/** 使用先序遍历和后序遍历创建一颗树 */
void CreatTree(Bitree** root)
{
//默认 *root = NULL
Bitree **ptr = root; //工作指针
Bitree *p = NULL; //出栈指针
int n, i, j;
int A[MAX_SIZE] = {0}, B[MAX_SIZE] = {0}; //两个序列都存放在数组里面
Bitree* stack[MAX_SIZE];
int ps = -1; //栈顶指针
printf("输入结点数量:");
scanf("%d", &n);
for(i = 0; i < n; i++) //输入
scanf("%d", &A[i]);
for(i = 0; i < n; i++)
scanf("%d", &B[i]);
i = 0, j = 0;
while(j < n) //创建
{
(*ptr) = (Bitree*)malloc(sizeof(Bitree));
(*ptr)->data = A[i++];
(*ptr)->left = NULL;
(*ptr)->right = NULL;
stack[++ps] = *ptr; //入栈
ptr = &((*ptr)->left);
while(ps >= 0 && stack[ps]->data == B[j])
{
p = stack[ps--]; //出栈
ptr = &(p->right);
j++;
}
}
}