[数据结构与算法]在归并排序中对小数组采用插入排序（算法导论课后思考题）

算法导论课后习题及其实现

第二章课后思考题 2-1

• a：插入排序的一般的时间复杂度为O($n^2$)，在最坏情况下（输入的数组完全逆序）假设其运行的时间为$T=a{n}^2+bn+c$(a,b,c为常数)。所以排序$n/k$个长度为$k$的数组需要的时间为$T_k=\frac{n}{k}(a{k}^2+bk+c)=ank+(b+\frac{c}{k})n$，所以其时间复杂度为O(nk)
• b：合并两个长度为k的子表需要的时间为O(k)，一共需要合并n/k个子表，所以需要的时间复杂度为O(n)。合并完成k个子表以后接下来需要合并n/2k个长度为2k的子表，所需要的时间复杂度依然为O(n)。一共需要合并lg(n/k)次才能完成排序。所以最终的时间复杂度为O(nlg(n/k))
• c：（没太看明白他想问啥，就聊聊我的理解吧）修改后的算法的时间复杂度为O(nk+nlg(n/k))表明是插入排序过程(O(nk))和合并过程(O(nlg(n/k)))的结合。当$k=an$，a为一个常数时（即k的值是关于n的一个线性函数时）其时间复杂度变为O($n^2$)。当k为一个常数时，其时间复杂度大致可以表示为O(nlgn)，其时间复杂度和普通归并排序相当，但当输入的规模变小时，由于常数项的影响选取合适的k值可以提升算法的运行效率。
• d：经过c题的分析，当k选取为合适的常数时可以提升算法效率，具体k的取值要基于需求输入的规模。

算法效率测试

算法效率测试基于（leetcode:921 sortArray）平台完成

首先是插入排序的算法效率：

    //插入排序, 时间复杂度O(n^2) 空间复杂度O(1), 插入排序对完全有序的序列时间复杂度会降低到O(n)
    public int[] sortArray(int[] nums) {
        for (int i = 1; i < nums.length; i++) {
            int now = nums[i];
            int j = i;
            while (j>0 && now < nums[j - 1]){
                nums[j] = nums[j-1];
                nums[j-1] = now;
                j--;
            }
        }
        return nums;
    }

然后是归并排序的算法效率测试

    public int[] sortArray(int[] nums) {
        mergeSort(nums, 0, nums.length-1);
        return nums;
    }

    void mergeSort(int[] nums, int left, int right){
        if(left <right){
            int mid = (left+right)/2;
            mergeSort(nums, left, mid);
            mergeSort(nums, mid + 1, right);
            merge(nums, left, mid, right);
        }
    }

    // 对nums数组进行归并操作
    void merge(int[] nums, int left, int mid, int right){
        int[] newArray = new int[right - left + 1];
        int p1 = left;
        int p2 = mid+1;
        int p = 0;
        while (p1 <= mid && p2 <= right) {
            if(nums[p1] < nums[p2]){
                newArray[p] = nums[p1];
                p1++;
            }else {
                newArray[p] = nums[p2];
                p2++;
            }
            p++;
        }
        if(p1 <= mid){
            System.arraycopy(nums, p1, newArray, p, mid-p1+1);
        }
        if(p2 <= right){
            System.arraycopy(nums, p2, newArray, p, right-p2+1);
        }
        System.arraycopy(newArray, 0, nums, left, newArray.length);
    }

可以看见算法效率大大提升！从1692ms变为10ms
最后测试一下优化版本的归并插入排序这里我选取的k的值是8（随便选的没啥根据，如果兄弟们对k值的设置有想法的可以评论区分享）

 public int[] sortArray(int[] nums) {
        mergeInsertSort(nums, 0, nums.length-1);
        return nums;
    }

    //归并插入排序, 时间复杂度O(nlgn(n)) 空间复杂度O(1)
    void mergeInsertSort(int[] nums, int left, int right){
        if(right - left > 8){
            int mid = (left+right)/2;
            mergeInsertSort(nums, left, mid);
            mergeInsertSort(nums, mid + 1, right);
            merge(nums, left, mid, right);
            return;
        }
        insertionSort(nums, left, right);
    }
    //插入排序, 时间复杂度O(n^2) 空间复杂度O(1), 插入排序对完全有序的序列时间复杂度会降低到O(n)
    void insertionSort(int[] nums, int left, int right){
        for (int i = left+1; i <= right; i++) {
            int now = nums[i];
            int j = i;
            while (j>left && now < nums[j - 1]){
                nums[j] = nums[j-1];
                nums[j-1] = now;
                j--;
            }
        }
    }
    // 对nums数组进行归并操作
    void merge(int[] nums, int left, int mid, int right){
        int[] newArray = new int[right - left + 1];
        int p1 = left;
        int p2 = mid+1;
        int p = 0;
        while (p1 <= mid && p2 <= right) {
            if(nums[p1] < nums[p2]){
                newArray[p] = nums[p1];
                p1++;
            }else {
                newArray[p] = nums[p2];
                p2++;
            }
            p++;
        }
        if(p1 <= mid){
            System.arraycopy(nums, p1, newArray, p, mid-p1+1);
        }
        if(p2 <= right){
            System.arraycopy(nums, p2, newArray, p, right-p2+1);
        }
        System.arraycopy(newArray, 0, nums, left, newArray.length);
    }

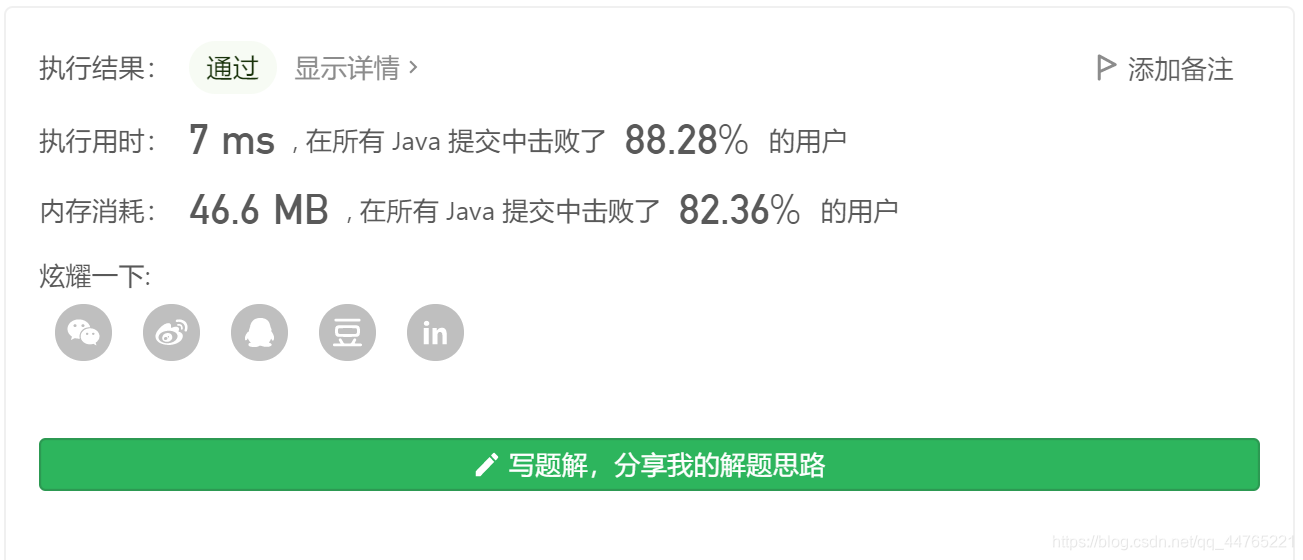
可以看到执行速度提升了3ms