[数据结构与算法]数据结构与算法（五）

第九章：贪心算法

leetcode455：分发饼干

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

示例 1:
输入: g = [1,2,3], s = [1,1]
输出: 1
解释:
你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
所以你应该输出1。

示例 2:
输入: g = [1,2], s = [1,2,3]
输出: 2
解释:
你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.

提示：

1 <= g.length <= 3 * 104
0 <= s.length <= 3 * 104
1 <= g[i], s[j] <= 231 - 1

【思路】

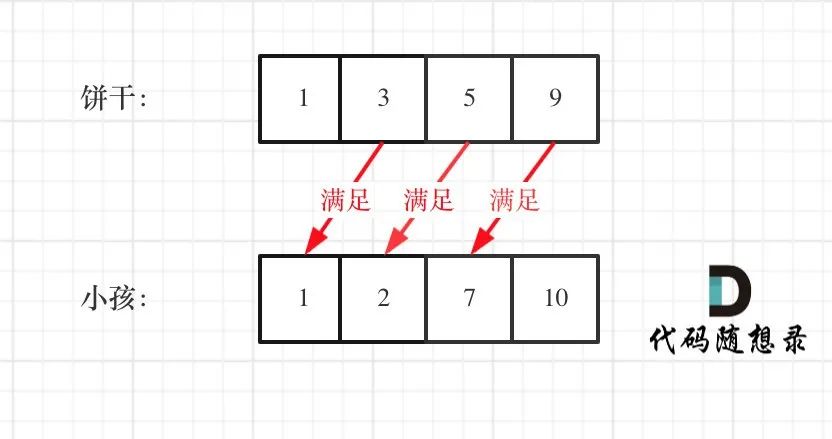
局部最优就是大饼干喂给胃口大的，充分利用饼干尺寸喂饱一个，全局最优就是喂饱尽可能多的小孩。

可以尝试使用贪心策略，先将饼干数组和小孩数组排序。

然后从后向前遍历小孩数组，用大饼干优先满足胃口大的，并统计满足小孩数量。

class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        //讲胃口值与尺寸进行排序，
        sort(g.begin(), g.end());//胃口值
        sort(s.begin(), s.end());//尺寸
        int g_index = g.size()-1;//胃口值坐标
        int s_index = s.size()-1;//尺寸值坐标
        int count = 0;//用于记录结果

        while(g_index >= 0 && s_index >= 0){
            //当尺寸大于胃口值时满足人数+1
            if(s[s_index] >= g[g_index]){
                count++;
                s_index--;
                g_index--;
                //否则缩小尺寸使之达到满足胃口值
            }else{
                g_index--;
            }
        }
        int a = 1;
        return count;        
    }
};

class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        //讲胃口值与尺寸进行排序，
        sort(g.begin(), g.end());//胃口值
        sort(s.begin(), s.end());//尺寸
        int g_index = g.size()-1;//胃口值坐标
        int s_index = s.size()-1;//尺寸值坐标
        int count = 0;//用于记录结果

        while(g_index >= 0 && s_index >= 0){
            //当尺寸大于胃口值时满足人数+1
            if(s[s_index] >= g[g_index]){
                count++;
                s_index--;
                g_index--;
                //否则缩小尺寸使之达到满足胃口值
            }else{
                g_index--;
            }
        }
        int a = 1;
        return count;        
    }
};

leetcode376：摆动序列

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为摆动序列。第一个差（如果存在的话）可能是正数或负数。少于两个元素的序列也是摆动序列。

例如， [1,7,4,9,2,5] 是一个摆动序列，因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

给定一个整数序列，返回作为摆动序列的最长子序列的长度。通过从原始序列中删除一些（也可以不删除）元素来获得子序列，剩下的元素保持其原始顺序。

示例 1:
输入: [1,7,4,9,2,5]
输出: 6
解释: 整个序列均为摆动序列。

示例 2:
输入: [1,17,5,10,13,15,10,5,16,8]
输出: 7
解释: 这个序列包含几个长度为 7 摆动序列，其中一个可为[1,17,10,13,10,16,8]。

示例 3:
输入: [1,2,3,4,5,6,7,8,9]
输出: 2

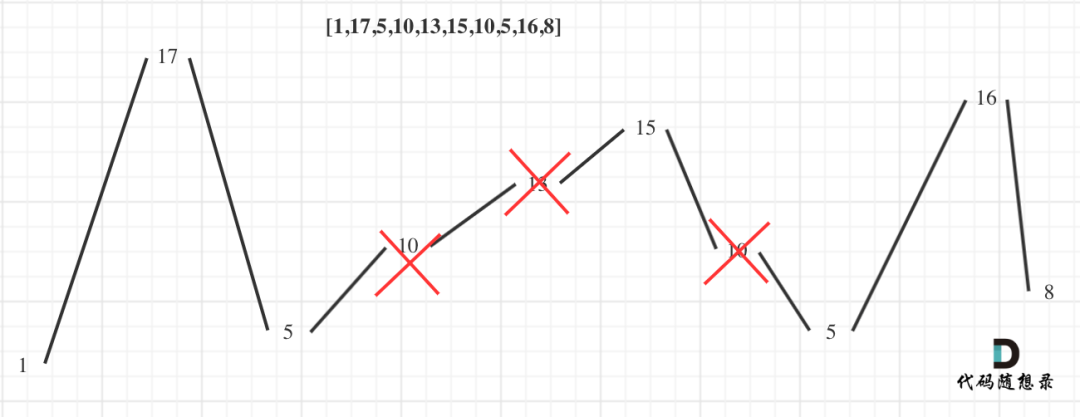
「局部最优：删除单调坡度上的节点（不包括单调坡度两端的节点），那么这个坡度就可以有两个局部峰值」。

「整体最优：整个序列有最多的局部峰值，从而达到最长摆动序列」。

「实际操作上，其实连删除的操作都不用做，因为题目要求的是最长摆动子序列的长度，所以只需要统计数组的峰值数量就可以了（相当于是删除单一坡度上的节点，然后统计长度）」

「这就是贪心所贪的地方，让峰值尽可能的保持峰值，然后删除单一坡度上的节点」。

例如序列[2,5]，它的峰值数量是2，如果靠统计差值来计算峰值个数就需要考虑数组最左面和最右面的特殊情况。

所以可以针对序列[2,5]，可以假设为[2,2,5]，这样它就有坡度了即preDiff = 0，如图：

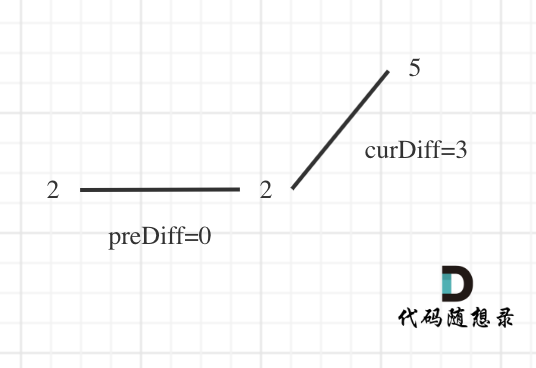
针对以上情形，result初始为1（默认最右面有一个峰值），此时curDiff > 0 && preDiff <= 0，那么result++（计算了左面的峰值），最后得到的result就是2（峰值个数为2即摆动序列长度为2）

//时间复杂度：O(n)
//空间复杂度：O(1)
class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        //异常处理
        if(nums.size() <= 1) 
            return nums.size();
        //初始化
        int curDiff = 0;    //当前差值
        int preDiff = 0;    //前一对差值
        int result = 1;     //记录峰值个数，序列默认序列最右边有一个峰值。
        
        for(int i = 1; i < nums.size(); i++){
            //计算当前峰值
            curDiff = nums[i] - nums[i-1];
            //出现峰值
            if((curDiff > 0 && preDiff <= 0) || (preDiff >= 0 && curDiff < 0)){
                result++;
                preDiff = curDiff;
            }
        }
        return result;
    }
};

保持区间波动，只需要把单调区间上的元素移除就可以了。

leetcode55：跳跃游戏

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个位置。

示例 1:
输入: [2,3,1,1,4]
输出: true
解释: 我们可以先跳 1 步，从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。

示例 2:
输入: [3,2,1,0,4]
输出: false
解释: 无论怎样，你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 ， 所以你永远不可能到达最后一个位置。

【思路】

其实跳几步无所谓，关键在于可跳的覆盖范围！

不一定非要明确一次究竟跳几步，每次取最大的跳跃步数，这个就是可以跳跃的覆盖范围。

这个范围内，别管是怎么跳的，反正一定可以跳过来。

「那么这个问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点！」

每次移动取最大跳跃步数（得到最大的覆盖范围），每移动一个单位，就更新最大覆盖范围。

「贪心算法局部最优解：每次取最大跳跃步数（取最大覆盖范围），整体最优解：最后得到整体最大覆盖范围，看是否能到终点」。

局部最优推出全局最优，找不出反例，试试贪心！

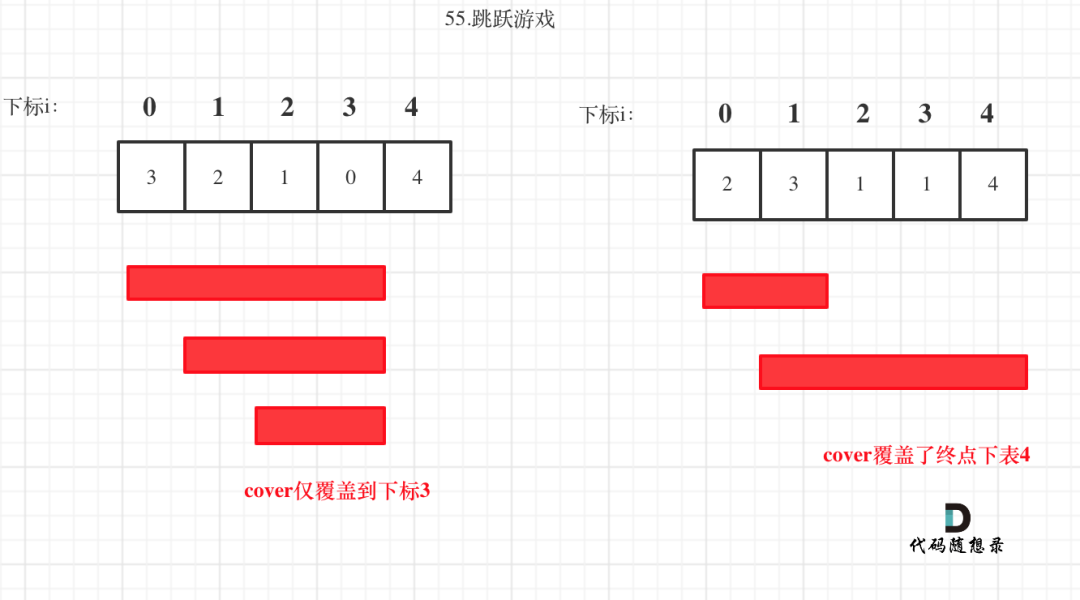
i每次移动只能在cover的范围内移动，每移动一个元素，cover得到该元素数值（新的覆盖范围）的补充，让i继续移动下去。

而cover每次只取 max(该元素数值补充后的范围, cover本身范围)。

如果cover大于等于了终点下标，直接return true就可以了。

class Solution {
public:
    bool canJump(vector<int>& nums) {
        //定义覆盖范围为0
        int cover = 0;
        if(nums.size() == 1) return true;//只有一个元素，就是能达到终点
        for(int i = 0; i <= cover; i++){//注意这里是小于等于cover
            //不断扩充cover的覆盖范围
            cover = max(i + nums[i], cover);
            //只要覆盖范围大于数组末尾下标直接返回true，否则返回false
            if(cover >= nums.size() - 1)
                return true;
        }
        return false;
    }
};

解题关键：不要考虑究竟跳多少步，而要考虑每次跳后的范围覆盖面积有多大

leetcode45：跳跃游戏II（动态规划）

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

你的目标是使用最少的跳跃次数到达数组的最后一个位置。

示例:
输入: [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

说明:
假设你总是可以到达数组的最后一个位置。

本题要计算最小步数，那么就要想清楚什么时候步数才一定要加一呢？

贪心的思路，局部最优：当前可移动距离尽可能多走，如果还没到终点，步数再加一。整体最优：一步尽可能多走，从而达到最小步数。

思路虽然是这样，但在写代码的时候还不能真的就能跳多远跳远，那样就不知道下一步最远能跳到哪里了。

「所以真正解题的时候，要从覆盖范围出发，不管怎么跳，覆盖范围内一定是可以跳到的，以最小的步数增加覆盖范围，覆盖范围一旦覆盖了终点，得到的就是最小步数！」

「这里需要统计两个覆盖范围，当前这一步的最大覆盖和下一步最大覆盖」。

如果移动下标达到了当前这一步的最大覆盖最远距离了，还没有到终点的话，那么就必须再走一步来增加覆盖范围，直到覆盖范围覆盖了终点。

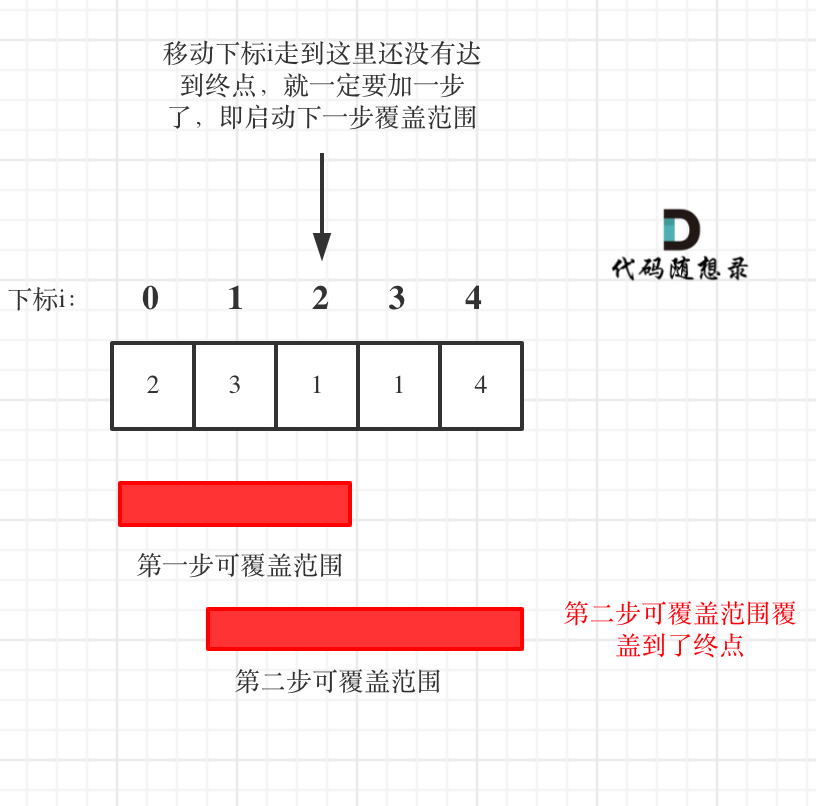
「图中覆盖范围的意义在于，只要红色的区域，最多两步一定可以到！（不用管具体怎么跳，反正一定可以跳到）」

从图中可以看出来，就是移动下标达到了当前覆盖的最远距离下标时，步数就要加一，来增加覆盖距离。最后的步数就是最少步数。

这里还是有个特殊情况需要考虑，当移动下标达到了当前覆盖的最远距离下标时

• 如果当前覆盖最远距离下标不是是集合终点，步数就加一，还需要继续走。
• 如果当前覆盖最远距离下标就是是集合终点，步数不用加一，因为不能再往后走了。

C++代码如下：（详细注释）

//方法一：贪心算法
class Solution {
public:
    int jump(vector<int>& nums) {
        int curcover = 0, nextcover = 0;
        int steps = 0;
        /*
        在遍历数组时，我们不访问最后一个元素，这是因为在访问最后一个元素之前，我们的边界一定大于等于最后一个位置，否则就无法跳到最后一个位置了。
        如果访问最后一个元素，在边界正好为最后一个位置的情况下，我们会增加一次「不必要的跳跃次数」，因此我们不必访问最后一个元素        
        */
        if(nums.size() == 1)
            return 0;
        for(int i = 0; i < nums.size(); i++)
        {
            nextcover = max(nextcover, nums[i] + i);    //更新当前覆盖最远距离下标
            if(i == curcover)//如果下标等于当前范围的终点时，步骤加一
            {
                curcover = nextcover;//下一个覆盖范围更新
                steps++;
                if(nextcover >= nums.size() - 1)
                    break;
                
            }
        }
        return steps;//返回步数
    }
};
//方法二：动态规划
class Solution {
public:
    int jump(vector<int>& nums) {
        int len = nums.size();
        //dp[i]:就是从0跳到i最少次数
        vector<int> dp(len);
        //动态数组dp的初始化
        dp[0] = 0;
        for(int i = 1; i < dp.size(); i++)
        {
            dp[i] = INT_MAX;
        }

        for(int i = 1; i < nums.size(); i++)
        {
            for(int j = 0; j < i; j++)
            {
                //如果从j这个位置条nums[j]步数如果大于优化位置i的话，证明能从j跳到i更新dp[i]的值，选取最小的步数
                if(j + nums[j] >= i)
                {
                    dp[i] = min(dp[i], dp[j] + 1);
                }
            }
        }
        return dp[len - 1];
    }
};

leetcode1306：跳跃游戏III

这里有一个非负整数数组 arr，你最开始位于该数组的起始下标 start 处。当你位于下标 i 处时，你可以跳到 i + arr[i] 或者 i - arr[i]。

请你判断自己是否能够跳到对应元素值为 0 的 任一 下标处。

注意，不管是什么情况下，你都无法跳到数组之外。

示例 1：

输入：arr = [4,2,3,0,3,1,2], start = 5
输出：true
解释：
到达值为 0 的下标 3 有以下可能方案：
下标 5 -> 下标 4 -> 下标 1 -> 下标 3
下标 5 -> 下标 6 -> 下标 4 -> 下标 1 -> 下标 3
示例 2：

输入：arr = [4,2,3,0,3,1,2], start = 0
输出：true
解释：
到达值为 0 的下标 3 有以下可能方案：
下标 0 -> 下标 4 -> 下标 1 -> 下标 3
示例 3：

输入：arr = [3,0,2,1,2], start = 2
输出：false
解释：无法到达值为 0 的下标 1 处。

提示：

1 <= arr.length <= 5 * 10^4
0 <= arr[i] < arr.length
0 <= start < arr.length

leetcode403：青蛙过河（动态规划）

一只青蛙想要过河。 假定河流被等分为若干个单元格，并且在每一个单元格内都有可能放有一块石子（也有可能没有）。 青蛙可以跳上石子，但是不可以跳入水中。

给你石子的位置列表 stones（用单元格序号 升序 表示）， 请判定青蛙能否成功过河（即能否在最后一步跳至最后一块石子上）。

开始时， 青蛙默认已站在第一块石子上，并可以假定它第一步只能跳跃一个单位（即只能从单元格 1 跳至单元格 2 ）。

如果青蛙上一步跳跃了 k 个单位，那么它接下来的跳跃距离只能选择为 k - 1、k 或 k + 1 个单位。 另请注意，青蛙只能向前方（终点的方向）跳跃。

示例 1：

输入：stones = [0,1,3,5,6,8,12,17]
输出：true
解释：青蛙可以成功过河，按照如下方案跳跃：跳 1 个单位到第 2 块石子, 然后跳 2 个单位到第 3 块石子, 接着 跳 2 个单位到第 4 块石子, 然后跳 3 个单位到第 6 块石子, 跳 4 个单位到第 7 块石子, 最后，跳 5 个单位到第 8 个石子（即最后一块石子）。
示例 2：

输入：stones = [0,1,2,3,4,8,9,11]
输出：false
解释：这是因为第 5 和第 6 个石子之间的间距太大，没有可选的方案供青蛙跳跃过去。

提示：

2 <= stones.length <= 2000
0 <= stones[i] <= 231 - 1
stones[0] == 0

class Solution {
    /*
    stones:石头下标不变
    n：石头长度不变
    u：当前所在石子的下标
    k：上一次是经过多少步跳到当前位置的
    return：是否能跳到最后一块石子
    */
    map<int, int> mp;
    map<int, bool> f;
    //记忆化深搜
    bool dfs(vector<int>& stones, int n, int u, int k)
    {
        int key = u * 10000 + k;
        if(f.count(key))
            return f[key];
        if(u == n - 1)
            return true;
        for(int i = -1; i <= 1; i++)
        {
            if(k + i == 0)
                continue;
            int next = stones[u] + k + i;
            if(mp.count(next))
            {
                bool cur = dfs(stones, n,mp[next],k + i);
                f[key] = cur;
                if(cur)
                    return true;
            }
        }
        f[key] = false;
        return false;
    }
public:
    bool canCross(vector<int>& stones) {
        //记录stones的大小
        int n = stones.size();
        if(stones[1] != 1)
            return false;
        for(int i = 0; i < n; i++)
        {
            mp[stones[i]] = i;
        }
        return dfs(stones, n, 1, 1);
    }
};

【动态规划解题思路】

1. 确定dp数组及下标含义

   dp[i] [k]: 表示当前在第i个位置，并且是以步长k跳到位置i时，是否达到最后一块石子

2. 确定递推公式

   dp[i] [k]是否为真，取决于上一个位置j的状态值，通过每次步长变化[-1,0,1]:

   dp[i] [k]可以从dp[j] [k-1]状态而来：先是经过k-1步跳跃到达j位置再在原步长k-1的基础上加1跳到位置i。

   dp[i] [k]可从dp[j] [k]状态而来：先是经过k步跳跃到达j位置，然后原步长不变，再跳一次跳到了位置i。

   dp[i] [k]可从dp[j] [k]状态而来：先是经过k+1步跳跃到达位置j，然后再原步长的基础上-1，跳到了位置i。

3. dp数组如何初始化

   初始化：dp[1] [1] = true;

4. 确定遍历顺序

   从递推公式可以看出，遍历的顺序是从上到下遍历的。

5. 举例dp数组

   略……………………

class Solution{
public:
	bool canCross(vector<int>& stones)
	{
		int n = stones.size();
		if (stones[1] != 1)	return false;
		//dp[i][speed]:表示能否一speed的速度，到达第i个石头
		vector<vector<bool>> dp(n, vector<bool>(n));//为什么是n*n大小的数组
		dp[0][0] = true;
		for (int i = 1; i < n; i++)
		{
			for (int j = 0; j < i; j++)//这里的j一定不能大于i吗？？？？
			{
				int k = stones[i] - stones[j];
				if (k <= 0 || k > j + 1)//为什么speed不能小于等于零尤其是等于，也不能大于j+1
					continue;//如果k-1>j的时候不进行操作，跳过此循环，stones[i] 到 stones[j]的距离最少要大于k-1
				dp[i][k] = dp[j][k - 1] || dp[j][k] || dp[j][k + 1];//判断从j是否能跳k-1或者k或者k+1步到达i
                //dp[i][k]代表从i跳到k步是否到达下一个石头上
			}
		}
        
		//当青蛙跳到最后一块石头时，无论是几步跳到这里的只要有一个成立就都成立
		for (int i = 1; i < n; i++)
		{
			if (dp[n - 1][i] == 1)
				return true;
		}
		return false;
	}
};

leetcode1005：K次取反后最大化的数组和

给定一个整数数组 A，我们只能用以下方法修改该数组：我们选择某个索引 i 并将 A[i] 替换为 -A[i]，然后总共重复这个过程 K 次。（我们可以多次选择同一个索引 i。）

以这种方式修改数组后，返回数组可能的最大和。

示例 1：输入：A = [4,2,3], K = 1
输出：5
解释：选择索引 (1,) ，然后 A 变为 [4,-2,3]。

示例 2：
输入：A = [3,-1,0,2], K = 3
输出：6
解释：选择索引 (1, 2, 2) ，然后 A 变为 [3,1,0,2]。

示例 3：
输入：A = [2,-3,-1,5,-4], K = 2
输出：13
解释：选择索引 (1, 4) ，然后 A 变为 [2,3,-1,5,4]。
  提示：

1 <= A.length <= 10000
1 <= K <= 10000
-100 <= A[i] <= 100

【思路】

贪心的思路，局部最优：让绝对值大的负数变为正数，当前数值达到最大，整体最优：整个数组和达到最大。

局部最优可以推出全局最优。

那么如果将负数都转变为正数了，K依然大于0，此时的问题是一个有序正整数序列，如何转变K次正负，让 数组和 达到最大。

那么又是一个贪心：局部最优：只找数值最小的正整数进行反转，当前数值可以达到最大（例如正整数数组{5, 3, 1}，反转1 得到-1 比 反转5得到的-5 大多了），全局最优：整个 数组和 达到最大。

那么本题的解题步骤为：

• 第一步：将数组按照绝对值大小从大到小排序，「注意要按照绝对值的大小」
• 第二步：从前向后遍历，遇到负数将其变为正数，同时K–
• 第三步：如果K还大于0，那么反复转变数值最小的元素，将K用完
• 第四步：求和

class Solution {
    static bool cmp(int a, int b){
        //前面的大于后面的所以是从大到小
        return abs(a) > abs(b);
    }
public:
    int largestSumAfterKNegations(vector<int>& A, int K) {
        int sum = 0;

        //第一步：将数组按照绝对值大小从大到小排序，一定是绝对值
        sort(A.begin(), A.end(), cmp);

        //第二步：从前向后遍历，遇到负数将其变为整数，同时K--；
        for(int i = 0; i < A.size(); i++){
            if(A[i] < 0 && K > 0){
                A[i] = -A[i];
                K--;
            }
        }

        //第三步：如果K还大于0，那么反复转表数组最小的元素，将K用完
        while(K--){
            //因为需求要求可以重复选择同一个索引
            //因为A是从大到小排序所以只需要不断改变末尾值将K给消耗完就可以了
            A[A.size() - 1] *= -1; 
        }

        //第四步：用于求和
        for(int i = 0; i < A.size(); i++){
            sum += A[i];
        }
        //返回结果
        return sum;
    }
};

「如果没有贪心的思考方式（局部最优，全局最优），很容易陷入贪心简单题凭感觉做，贪心难题直接不会做，其实这样就锻炼不了贪心的思考方式了」。

leetcode134：加油站

在一条环路上有 N 个加油站，其中第 i 个加油站有汽油 gas[i] 升。

你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。

如果你可以绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1。

说明:

如果题目有解，该答案即为唯一答案。
输入数组均为非空数组，且长度相同。
输入数组中的元素均为非负数。
示例 1:
输入:
gas  = [1,2,3,4,5]
cost = [3,4,5,1,2]

输出: 3
解释:
从 3 号加油站(索引为 3 处)出发，可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站，此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站，此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站，此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站，此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站，你需要消耗 5 升汽油，正好足够你返回到 3 号加油站。
因此，3 可为起始索引。

示例 2:
输入:
gas  = [2,3,4]
cost = [3,4,3]

输出: -1
解释:
你不能从 0 号或 1 号加油站出发，因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发，可以获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站，此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站，此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站，因为返程需要消耗 4 升汽油，但是你的油箱只有 3 升汽油。
因此，无论怎样，你都不可能绕环路行驶一周。

【解题思路】

方法一：暴力法

遍历每一个加油站为起点的情况，模拟一圈。如果跑了一圈，中途没有断油，而且最后油量大于等于0，说明这个起点是是ok的。

for循环适合模拟从头到尾的遍历，而while循环适合模拟环形遍历

//时间复杂度：O(n^2)
//空间复杂度：O(n)
class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        for(int i = 0; i < cost.size(); i++){
            int rest = gas[i] - cost[i];//记录剩余油量
            int index = (i + 1) % cost.size();
            while(rest > 0 && index != i){//模拟以i为起点行驶一圈
                rest += gas[index] - cost[index];
                index = (index + 1) % cost.size();
            }
            //如果以i为起点跑一圈，剩余油量大于等于0，返回起始位置
            if(rest >= 0 && index == i) 
                return i;
        }
        return -1;
    }
};

方法二：贪心算法

直接从全局进行贪心选择，情况如下：

• 情况一：如果gas的总和小于cost总和，那么无论从哪里出发，一定是跑不了一圈的
• 情况二：rest[i] = gas[i]-cost[i]为一天剩下的油，i从0开始计算累加到最后一站，如果累加没有出现负数，说明从0出发，油就没有断过，那么0就是起点。
• 情况三：如果累加的最小值是负数，汽车就要从非0节点出发，从后向前，看哪个节点能这个负数填平，能把这个负数填平的节点就是出发节点。

C++代码：

//时间复杂度：O(n)
//空间复杂度：O(1)
class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        int curSum = 0;
        int min = INT_MAX; // 从起点出发，油箱里的油量最小值
        for (int i = 0; i < gas.size(); i++) {
            int rest = gas[i] - cost[i];
            curSum += rest;
            if (curSum < min) {
                min = curSum;
            }
        }
        if (curSum < 0) return -1;  // 情况1
        if (min >= 0) return 0;     // 情况2
                                    // 情况3
        for (int i = gas.size() - 1; i >= 0; i--) {
            int rest = gas[i] - cost[i];
            min += rest; 
            if (min >= 0) {
                return i;
            }
        }
        return -1;
    }
};

方法三：贪心算法

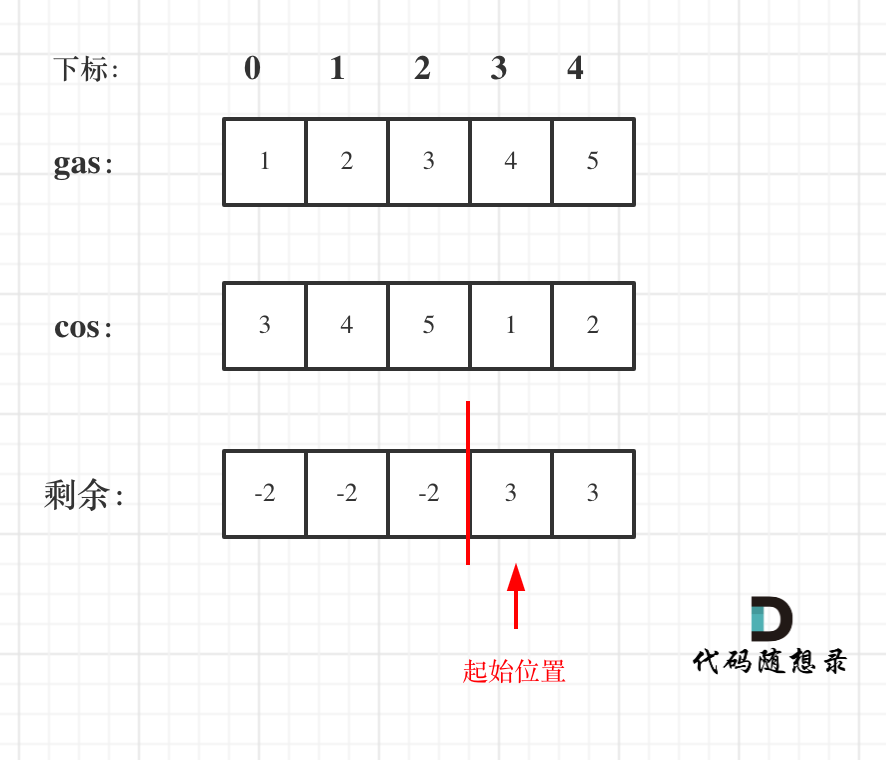
可以换一个思路，首先如果总油量减去总消耗大于等于零那么一定可以跑完一圈，说明 各个站点的加油站 剩油量rest[i]相加一定是大于等于零的。

每个加油站的剩余量rest[i]为gas[i] - cost[i]。

i从0开始累加rest[i]，和记为curSum，一旦curSum小于零，说明**[0, i]区间都不能作为起始位置，起始位置从i+1算起，再从0计算curSum。**

如果出现更大的负数，就是更新j，那么起始位置又变成新的j+1了。

而且j之前出现了多少负数，j后面就会出现多少正数，因为耗油总和是大于零的（前提我们已经确定了一定可以跑完全程）。

「那么局部最优：当前累加rest[j]的和curSum一旦小于0，起始位置至少要是j+1，因为从j开始一定不行。全局最优：找到可以跑一圈的起始位置」。

//时间复杂度：O(n)
//空间复杂度：O(1)
class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        //初始化
        //当前节点的剩余油量和
        int curSum = 0; 
        //总剩余油量和
        int totalSum = 0;
        //开始位置
        int start = 0;
        
        //遍历加油站
        for(int i = 0; i < gas.size(); i++){
            curSum += gas[i] - cost[i];
            totalSum += gas[i]  - cost[i];

            //当前累加rest[i]和curSum一旦小于0
            if(curSum < 0){//说明从该加油站是不能走到下一加油站的
                //起始位置更新为i+1
                start = i + 1;
                //curSum从0开始，重新计算
                curSum = 0;
            }
        }
        
        if(totalSum < 0)
            //说明怎么走都不可能跑一圈
            return -1;
        return start;
    }
};

leetcode135：分发糖果

老师想给孩子们分发糖果，有 N 个孩子站成了一条直线，老师会根据每个孩子的表现，预先给他们评分。

你需要按照以下要求，帮助老师给这些孩子分发糖果：

每个孩子至少分配到 1 个糖果。
相邻的孩子中，评分高的孩子必须获得更多的糖果。
那么这样下来，老师至少需要准备多少颗糖果呢？

示例 1:
输入: [1,0,2]
输出: 5
解释: 你可以分别给这三个孩子分发 2、1、2 颗糖果。

示例 2:
输入: [1,2,2]
输出: 4
解释: 你可以分别给这三个孩子分发 1、2、1 颗糖果。
第三个孩子只得到 1 颗糖果，这已满足上述两个条件。

【思路】

该类题目一定要确定一边之后再确定另一边，比如比较每个孩子的左边，然后再比较右边，如果两边一起考虑一定会顾此失彼。

先确定右边评分大于左边的情况（也就是从前向后遍历）

此时局部最优：只要右边评分比左边大，右边的孩子就多一个糖果，全局最优：相邻的孩子中，评分高的右孩子获得比左边孩子更多的糖果

所有有：如果**ratings[i] > ratings[i-1]**那么[i]的糖一定要比[i-1]的糖要多一个，所以贪心：candyVec[i] = candyVec[i-1] + 1;

//从前向后
for(int i = 1; i < ratings.size(); i++){
	if(ratings[i] > ratings[i-1])
		candyVec[i] = candyVec[i-1] + 1;
}

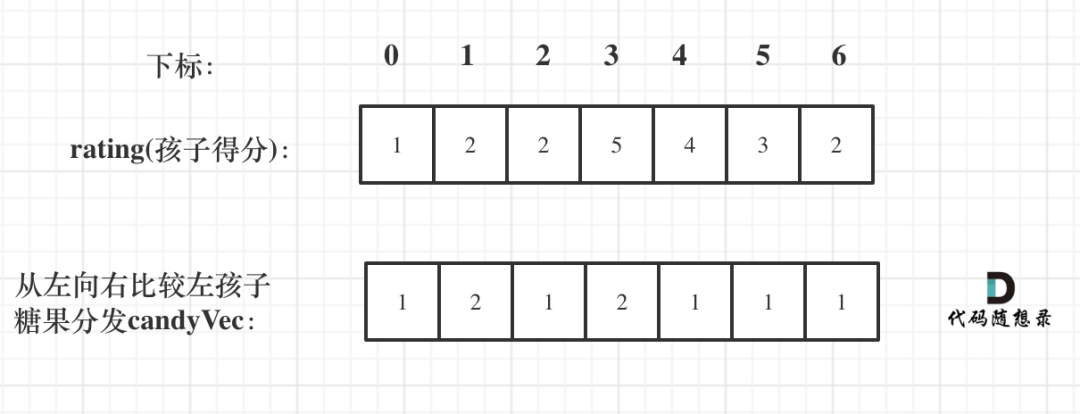
因为如果从前向后遍历，根据 ratings[i + 1] 来确定 ratings[i] 对应的糖果，那么每次都不能利用上前一次的比较结果了。

「确定左孩子大于右孩子的情况一定要从后向前遍历！」

如果 ratings[i] > ratings[i + 1]，此时candyVec[i]（第i个小孩的糖果数量）就有两个选择了，一个是candyVec[i + 1] + 1（从右边这个加1得到的糖果数量），一个是candyVec[i]（之前比较右孩子大于左孩子得到的糖果数量）。

那么又要贪心了，局部最优：取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量，保证第i个小孩的糖果数量即大于左边的也大于右边的。全局最优：相邻的孩子中，评分高的孩子获得更多的糖果。

局部最优可以推出全局最优。

所以就取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量，「candyVec[i]只有取最大的才能既保持对左边candyVec[i - 1]的糖果多，也比右边candyVec[i + 1]的糖果多」。

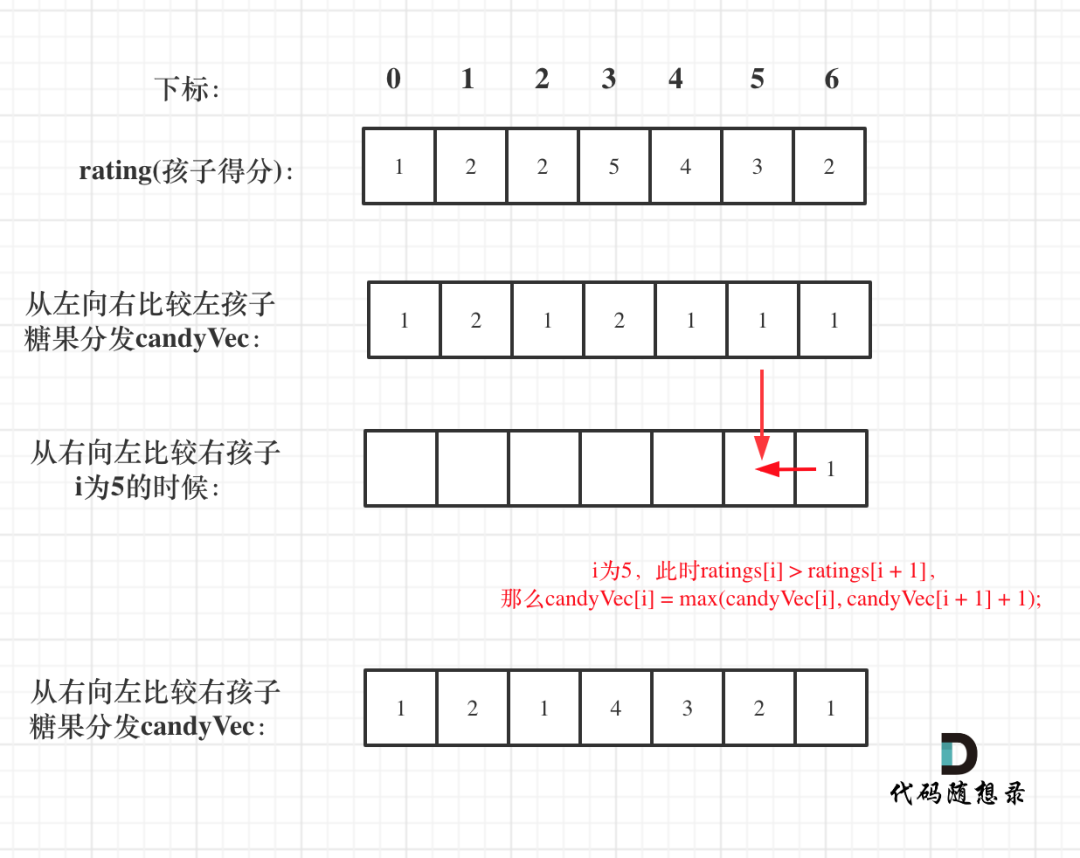
// 从后向前
for (int i = ratings.size() - 2; i >= 0; i--) {
    if (ratings[i] > ratings[i + 1] ) {
        candyVec[i] = max(candyVec[i], candyVec[i + 1] + 1);
    }
}

class Solution {
public:
    int candy(vector<int>& ratings) {
        int len = ratings.size();
        //因为需求说明每名同学最少分1颗糖果
        vector<int> candyVec(len, 1);
        int sum = 0;
        //从左向右遍历，保证右边分多的同学比左边的同学分的糖果要多
        for(int i = 1; i < len; i++){
            if(ratings[i] > ratings[i-1])
                candyVec[i] = candyVec[i-1] + 1;
        }
        //从右向左遍历，保证左边分多的同学比右边同学分的糖果要多
        for(int i = len - 2; i >= 0; i--){
            //易错点如果输入数据 1 3 2 2 1-》candy= 1 2 1 2 1如果不加入限定条件则candy 1 3 1 2 1；iindex为1的值左遍历于右遍历都加1了，重复了
            if(ratings[i] > ratings[i+1] && candyVec[i] <= candyVec[i+1])
                candyVec[i] = candyVec[i+1] + 1;
        }
        //遍历求分发糖果的总和
        for(int i = 0; i < candyVec.size(); i++){
            sum += candyVec[i];
        }
        return sum;
    }
};

那么本题我采用了两次贪心的策略：

• 一次是从左到右遍历，只比较右边孩子评分比左边大的情况。
• 一次是从右到左遍历，只比较左边孩子评分比右边大的情况。

这样从局部最优推出了全局最优，即：相邻的孩子中，评分高的孩子获得更多的糖果。

leetcode860：柠檬水找零

在柠檬水摊上，每一杯柠檬水的售价为 5 美元。

顾客排队购买你的产品，（按账单 bills 支付的顺序）一次购买一杯。

每位顾客只买一杯柠檬水，然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零，也就是说净交易是每位顾客向你支付 5 美元。

注意，一开始你手头没有任何零钱。

如果你能给每位顾客正确找零，返回 true ，否则返回 false 。

示例 1：
输入：[5,5,5,10,20]
输出：true
解释：
前 3 位顾客那里，我们按顺序收取 3 张 5 美元的钞票。
第 4 位顾客那里，我们收取一张 10 美元的钞票，并返还 5 美元。
第 5 位顾客那里，我们找还一张 10 美元的钞票和一张 5 美元的钞票。
由于所有客户都得到了正确的找零，所以我们输出 true。

示例 2：
输入：[5,5,10]
输出：true

示例 3：
输入：[10,10]
输出：false

示例 4：
输入：[5,5,10,10,20]
输出：false
解释：
前 2 位顾客那里，我们按顺序收取 2 张 5 美元的钞票。
对于接下来的 2 位顾客，我们收取一张 10 美元的钞票，然后返还 5 美元。
对于最后一位顾客，我们无法退回 15 美元，因为我们现在只有两张 10 美元的钞票。
由于不是每位顾客都得到了正确的找零，所以答案是 false。

提示：

0 <= bills.length <= 10000
bills[i] 不是 5 就是 10 或是 20

【思路】

只需要维护三种金额的数量，5，10和20。

有如下三种情况：

• 情况一：账单是5，直接收下。
• 情况二：账单是10，消耗一个5，增加一个10
• 情况三：账单是20，优先消耗一个10和一个5，如果不够，再消耗三个5

而情况三逻辑也不复杂甚至感觉纯模拟就可以了，其实情况三这里是有贪心的。

账单是20的情况，为什么要优先消耗一个10和一个5呢？

「因为美元10只能给账单20找零，而美元5可以给账单10和账单20找零，美元5更万能！」

所以局部最优：遇到账单20，优先消耗美元10，完成本次找零。全局最优：完成全部账单的找零。

局部最优可以推出全局最优，并找不出反例，那么就试试贪心算法！

class Solution {
public:
    bool lemonadeChange(vector<int>& bills) {
        //用moneymap来存储5元10元20元金钱的个数
        unordered_map<int,int> money;
        //按支付顺序遍历遍历账单
        for(int i = 0; i < bills.size(); i++){
            //将当前支付的金钱存入moneymap中key为金钱，value为Key对应的个数
            money[bills[i]]++;
            //情况一：如果支付的是10元，只能用5元来找零，如果没有则返回false
            if(bills[i] == 10){
                if(money[5] >= 1)
                    money[5]--;
                else
                    return false;
            }
            //情况二:如果支付的是20元，有两种找零方法，一种是用十元找零优先级最高，另一种是用5元找零
            if(bills[i] == 20){
                if(money[10] > 0 && money[5] > 0){
                    //优先使用10元找零
                    money[10]--;
                    money[5]--;
                }else if(money[10] == 0 && money[5] >= 3){
                    //没有10元只用5元找零
                    money[5] = money[5] - 3;
                } else
                    //既不能用10元也不能用5元则返回false
                        return false;
            }
        }
        //否则返回true
        return true;
    }
};

重叠区间

leetcode406：根据身高重建队列

假设有打乱顺序的一群人站成一个队列，数组 people 表示队列中一些人的属性（不一定按顺序）。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ，前面 正好 有 ki 个身高大于或等于 hi 的人。

请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ，其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性（queue[0] 是排在队列前面的人）。

示例 1：
输入：people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出：[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
解释：
编号为 0 的人身高为 5 ，没有身高更高或者相同的人排在他前面。
编号为 1 的人身高为 7 ，没有身高更高或者相同的人排在他前面。
编号为 2 的人身高为 5 ，有 2 个身高更高或者相同的人排在他前面，即编号为 0 和 1 的人。
编号为 3 的人身高为 6 ，有 1 个身高更高或者相同的人排在他前面，即编号为 1 的人。
编号为 4 的人身高为 4 ，有 4 个身高更高或者相同的人排在他前面，即编号为 0、1、2、3 的人。
编号为 5 的人身高为 7 ，有 1 个身高更高或者相同的人排在他前面，即编号为 1 的人。
因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。

示例 2：
输入：people = [[6,0],[5,0],[4,0],[3,2],[2,2],[1,4]]
输出：[[4,0],[5,0],[2,2],[3,2],[1,4],[6,0]]

提示：

1 <= people.length <= 2000
0 <= hi <= 10^6
0 <= ki < people.length
题目数据确保队列可以被重建

【思路】

本题有俩个个维度，h与k，看到这种题目一定要想如何确定一个维度，然后按照另一个维度重新排列。

遇到两个维度权衡的时候，一定要先确定一个维度，再确定另一个维度。

按照身高h来排序呢，身高一定是从大到小排（身高相同的话则k小的站前面），让高个子在前面。

只需要按照K为下标重新插入队列就可以了。

按照身高排序之后，优先按身高高的people的k来插入，后序插入节点也不会影响前面已经插入的节点，最终按照k的规则完成了队列。

所以在按照身高从大到小排序后：

「局部最优：优先按身高高的people的k来插入。插入操作过后的people满足队列属性」

「全局最优：最后都做完插入操作，整个队列满足题目队列属性」

排序完的people：
[[7,0], [7,1], [6,1], [5,0], [5,2]，[4,4]]

插入的过程：
插入[7,0]：[[7,0]]
插入[7,1]：[[7,0],[7,1]]
插入[6,1]：[[7,0],[6,1],[7,1]]
插入[5,0]：[[5,0],[7,0],[6,1],[7,1]]
插入[5,2]：[[5,0],[7,0],[5,2],[6,1],[7,1]]
插入[4,4]：[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]

此时就按照题目的要求完成了重新排列。

//时间复杂度：O(nlogn + n^2)
//空间复杂度：O(n)
// 版本一
class Solution {
    static bool cmp(const vector<int>& a, const vector<int>& b){
        //a[0]身高，a[1]身高排在他前面人的个数
        //优先比较身高，升高相同比较按照排在他前面人身高的个数从小到大排列
        if(a[0] == b[0])
            return a[1] < b[1];//第二个大于第一个所以是递增的
        return a[0] > b[0];//第一个大于第二个所以是递减
    }
public:
    vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
        //按照自定义排序方式进行排序
        //第一步：先按照身高从大到小排列，身高相同按照比他高的个数从小到大排序
        sort(people.begin(), people.end(), cmp);
        vector<vector<int>> que;

        for(int i = 0; i < people.size(); i++){
            //position 是people中排在他前面的人的个数
            int position = people[i][1];
            que.insert(que.begin() + position, people[i]);
        }
        return que;
    }
};

使用vector是非常费时的，C++中vector（可以理解是一个动态数组，底层是普通数组实现的）如果插入元素大于预先普通数组大小，vector底部会有一个扩容的操作，即申请两倍于原先普通数组的大小，然后把数据拷贝到另一个更大的数组上。

所以使用vector（动态数组）来insert，是费时的，插入再拷贝的话，**单纯一个插入的操作就是O(n^{2)了，**甚至可能拷贝好几次，就不止O(n}2)了。

所以优化更改数据结构：

将动态数组改为链表：

//时间复杂度：O(nlogn + n^2)
//空间复杂度：O(n)
// 版本二
class Solution {
public:
    // 身高从大到小排（身高相同k小的站前面）
    static bool cmp(const vector<int> a, const vector<int> b) {
        if (a[0] == b[0]) return a[1] < b[1];
        return a[0] > b[0];
    }
    vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
        sort (people.begin(), people.end(), cmp);
        
        //与上一种方法不同
        list<vector<int>> que; // list底层是链表实现，插入效率比vector高的多
        
        for (int i = 0; i < people.size(); i++) {
            int position = people[i][1]; // 插入到下标为position的位置
            std::list<vector<int>>::iterator it = que.begin();
            //寻找插入位置
            while (position--) { // 寻找在插入位置
                it++; 
            }
            //再找到的位置上插入people元素
            que.insert(it, people[i]); 
        }
        //将链表转成vector
        return vector<vector<int>>(que.begin(), que.end());
    }
};

「对使用某一种语言容器的使用，特性的选择都会不同程度上影响效率」。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VNg50Keb-1626103523417)(C:\Users\mubao\AppData\Roaming\Typora\typora-user-images\image-20210325170206393.png)]

leetcode452：用最少数量的箭引爆气球–》求重叠区间

在二维空间中有许多球形的气球。对于每个气球，提供的输入是水平方向上，气球直径的开始和结束坐标。

由于它是水平的，所以纵坐标并不重要，因此只要知道开始和结束的横坐标就足够了。开始坐标总是小于结束坐标。

一支弓箭可以沿着 x 轴从不同点完全垂直地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 xstart，xend， 且满足  xstart ≤ x ≤ xend，则该气球会被引爆。

可以射出的弓箭的数量没有限制。弓箭一旦被射出之后，可以无限地前进。我们想找到使得所有气球全部被引爆，所需的弓箭的最小数量。

给你一个数组 points ，其中 points [i] = [xstart,xend] ，返回引爆所有气球所必须射出的最小弓箭数。

示例 1：
输入：points = [[10,16],[2,8],[1,6],[7,12]]

输出：2
解释：对于该样例，x = 6 可以射爆 [2,8],[1,6] 两个气球，以及 x = 11 射爆另外两个气球

示例 2：
输入：points = [[1,2],[3,4],[5,6],[7,8]]
输出：4

示例 3：
输入：points = [[1,2],[2,3],[3,4],[4,5]]
输出：2

示例 4：
输入：points = [[1,2]]
输出：1

示例 5：
输入：points = [[2,3],[2,3]]
输出：1

提示：

0 <= points.length <= 10^4
points[i].length == 2
-2^31 <= xstart < xend <= 2^31 - 1

【思路】

局部最优：当气球出现重叠，一起射，所用弓箭最少。全局最优：把所有气球射爆所用弓箭最少。

如何模拟气球射爆的过程呢？是在数组中移除元素还是做标记呢？

仔细思考一下就发现：如果把气球排序之后，从前到后遍历气球，被射过的气球仅仅跳过就行了，没有必要让气球数组remote气球，只要记录一下箭的数量就可以了。

「为了让气球尽可能的重叠，需要对数组进行排序」。

「如果气球重叠了，重叠气球中右边边界的最小值 之前的区间一定需要一个弓箭」。

以题目示例：[[10,16],[2,8],[1,6],[7,12]]为例，如图：（方便起见，已经排序）

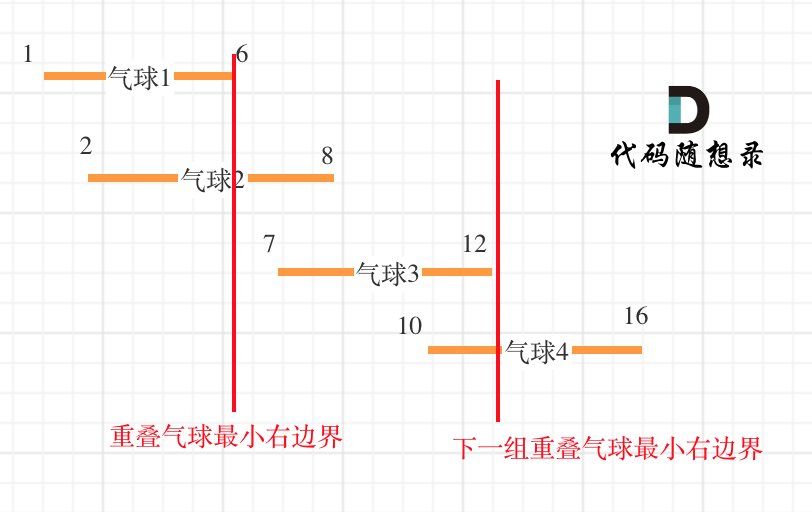
可以看出首先第一组重叠气球，一定是需要一个箭，气球3，的左边界大于了 第一组重叠气球的最小右边界，所以再需要一支箭来射气球3了。

//时间复杂度：O(nlogn),因为有一个快排
//空间复杂度：O(1)
class Solution {
    //自定义排序需求，从小到大排序
    static bool cmp(vector<int>& a, vector<int>& b){
        return a[0] < b[0];
    }
public:
    int findMinArrowShots(vector<vector<int>>& points) {
        //异常处理
        if(points.size() == 0) return 0;
        //points不为空至少需要一只箭
        //无论是有一个气球还是两个气球初始都需要一只箭来射破
        int count = 1;

        sort(points.begin(), points.end(), cmp);

        for(int i = 1; i < points.size(); i++){
            //[1,2]与[3,5]此时就需要两只箭来设这个气球
            if(points[i][0] > points[i-1][1]){//气球i和气球i-1不挨着，注意这里不是>=
                count++;//需要一只箭
            }
            //points[i][0] <= points[i-1][1]
            //[1,2][2,3]或者[1,3][2,4]这两种情况，此时就选择气球有重叠边界
            else{//气球i与气球i-1挨着，选取重叠边界，因为默认需要一只箭，所以让此时重叠的右边界与下一时刻的左边界对比
                points[i][1] = min(points[i-1][1], points[i][1]);//更新重叠气球最小右边界
            }
        }
        return count;
    }
};

注意题目中说的是：满足 xstart ≤ x ≤ xend，则该气球会被引爆。那么说明两个气球挨在一起不重叠也可以一起射爆，

所以代码中 if (points[i][0] > points[i - 1][1]) 不能是>=

leetcode435：无重叠区间

【题目】

给定一个区间的集合，找到需要移除区间的最小数量，使剩余区间互不重叠。

注意:

可以认为区间的终点总是大于它的起点。
【自己思考】-》边界相邻是否认为区间重叠？？？区间 [1,2] 和 [2,3] 的边界相互“接触”，但没有相互重叠。
示例 1:

输入: [ [1,2], [2,3], [3,4], [1,3] ]

输出: 1

解释: 移除 [1,3] 后，剩下的区间没有重叠。
示例 2:

输入: [ [1,2], [1,2], [1,2] ]

输出: 2

解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
示例 3:

输入: [ [1,2], [2,3] ]

输出: 0

解释: 你不需要移除任何区间，因为它们已经是无重叠的了。

//时间复杂度：O(nlogn)
//空间复杂度：O(1)
class Solution {
    static bool cmp(vector<int>& a, vector<int>& b){
        return a[0] < b[0];
    }
public:
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        //初始化
        int len = intervals.size();
        int result = 0;
        //异常处理
        if(len <= 1)return 0;
        //按照a[i][?]的顺序从小到大排列
        sort(intervals.begin(), intervals.end(), cmp);
        //之后遍历数组，又重复区间就移除
        for(int i = 1; i < len; i++){
            //出现重叠区间了
            if(intervals[i][0] < intervals[i-1][1])
            {
                result++;
                //正常需要将重复区间的数组移除，但是移除很麻烦，所以将最大值变为最小值赋值，就可以解决下一次循环用错数组的问题了。
                intervals[i][1] = min(intervals[i-1][1], intervals[i][1]);
            }
        }
        //返回结果
        return result;
    }
};

leetcode763：划分字母区间

**字符串 S 由小写字母组成。**我们要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。返回一个表示每个字符串片段的长度的列表。

示例：
输入：S = “ababcbacadefegdehijhklij”
输出：[9,7,8]
解释：
划分结果为 “ababcbaca”, “defegde”, “hijhklij”。
每个字母最多出现在一个片段中。
像 “ababcbacadefegde”, “hijhklij” 的划分是错误的，因为划分的片段数较少。

提示：

• S的长度在[1, 500]之间。
• S只包含小写字母 ‘a’ 到 ‘z’ 。

【思路】

一想到分割字符串就想到了回溯，但本题其实不用回溯去暴力搜索。

题目要求同一字母最多出现在一个片段中，那么如何把同一个字母的都圈在同一个区间里呢？

如果没有接触过这种题目的话，还挺有难度的。

在遍历的过程中相当于是要找每一个字母的边界，「如果找到之前遍历过的所有字母的最远边界，说明这个边界就是分割点了」。此时前面出现过所有字母，最远也就到这个边界了。

可以分为如下两步：

• 统计每一个字符最后出现的位置
• 从头遍历字符，并更新字符的最远出现下标，如果找到字符最远出现位置下标和当前下标相等了，则找到了分割点

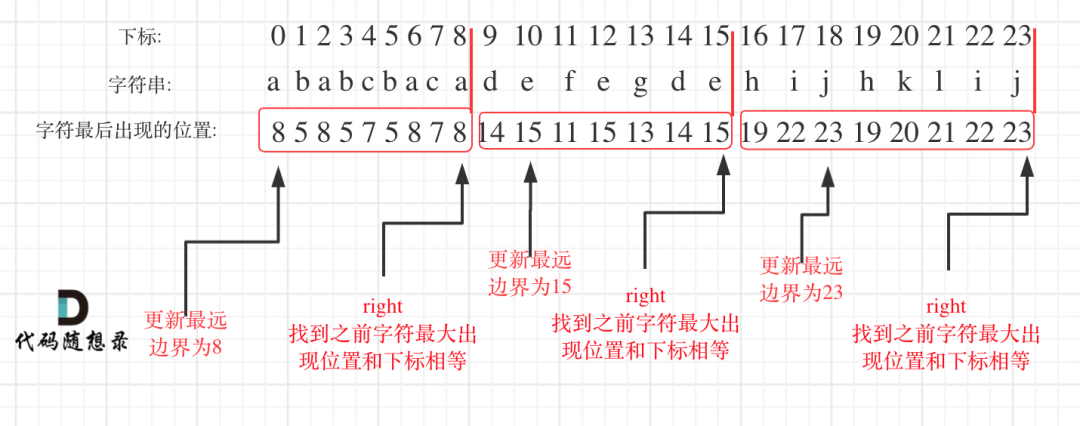
class Solution {
    /*
    //输入：字符char，要求返回输出：字符在字符串中的最后位置的下标
    int get_last_index(string S, char c, int index){
        int lastindex = INT_MIN;
        for(int i = index + 1; i < S.size(); i++){
            if(S[i] == c){
                lastindex = max(lastindex, i);
            }
        }
        return lastindex;
    }*/
public:
    vector<int> partitionLabels(string S) {

        //hash[i]用来为出现的字符存储最后的位置
        int hash[27] = {0};

        //统计每个字符最后出现的位置
        for(int i = 0; i < S.size(); i++){
            //因为后出现的字符会将前面的字符覆盖，所以可以用这正方法求解
            hash[S[i] - 'a'] = i;
        }

        //初始化变量
        vector<int> result;
        int left = 0;
        int right = 0;

        //进行遍历整个S数组
        for(int i = 0; i < S.size(); i++){
            //找到出现最远的下标并更新，因为i是不断增加的，所以可能在i到right之前后更大的下标，这时就要更新更大的right
            right = max(right, hash[S[i] - 'a']);//寻找最大的right
            //"ababcbacadefegdehijhklij"
            //         ^如果i遍历到这里此时说明同一字母都出现在i之前，i之后没有前面的字母啦
            if(i == right){
                // "ababcbacadefegdehijhklij"->
                //left = 0; right = 8第一次插入 8 - 0 + 1=9
                //left = right + 1= 9,right = 15 第二次插入：15 - 9 + 1 = 7；
                //同理，第三次插入：23 - 16 + 1 = 8
                result.push_back(right - left + 1);
                left = i + 1;
            }
        }
        return result;
    }
};

leetcode56：合并区间

【题目】

给出一个区间的集合，请合并所有重叠的区间。

示例 1:
输入: intervals = [[1,3],[2,6],[8,10],[15,18]]
输出: [[1,6],[8,10],[15,18]]
解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

示例 2:
输入: intervals = [[1,4],[4,5]]
输出: [[1,5]]
解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。
注意：输入类型已于2019年4月15日更改。请重置默认代码定义以获取新方法签名。

提示：

• intervals[i] [0] <= intervals[i] [1]

【思路】

按照左边界排序，排序之后局部最优：每次合并都取最大的右边界，这样就可以合并更多的区间了，整体最优：合并所有重叠的区间。

按照左边界从小到大排序之后，如果 intervals[i][0] < intervals[i - 1][1] 即intervals[i]左边界 < intervals[i - 1]右边界，则一定有重复，因为intervals[i]的左边界一定是大于等于intervals[i - 1]的左边界。

即：intervals[i]的左边界在intervals[i - 1]左边界和右边界的范围内，那么一定有重复！

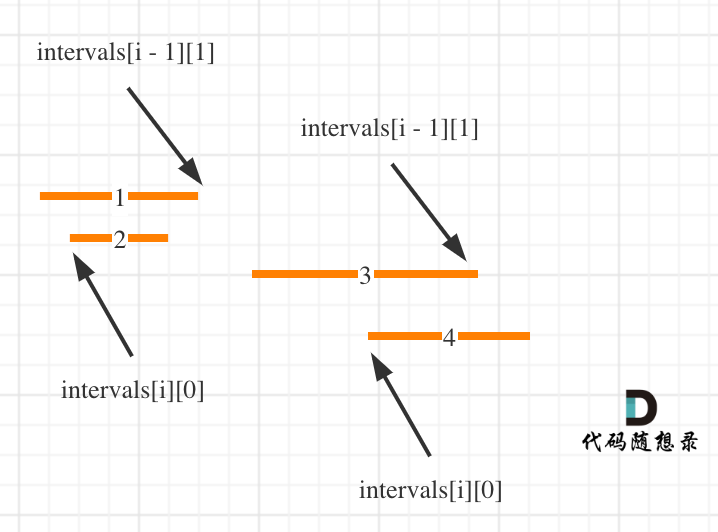
其实就是用合并区间后左边界和右边界，作为一个新的区间，加入到result数组里就可以了。如果没有合并就把原区间加入到result数组。

class Solution {
    static bool cmp(const vector<int>& a, const vector<int>& b){
        return a[0]<b[0];
    }
public:
/*
    情况一：[1,3] [2,4]
    情况二：[1,4] [2,3]
    情况三：[1,3] [4,5]
    情况四：[1,4] [2,5] [6,7]
*/
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        int len = intervals.size();
        //初始化result数组用于返回值
        vector<vector<int>> result;
        //异常处理
        if(len == 0)
            return result;
        //按照自定义的cmp进行排序
        sort(intervals.begin(), intervals.end(), cmp);

        //标记最后一个区间有没有合并
        bool flag = false;

        for(int i = 1; i < len; i++){
            int start = intervals[i-1][0];//初始化为i-1区间的左边界
            int end = intervals[i-1][1];//初始化i-1区间的右边界

            //[1,3][2,4]
            while(i < len && intervals[i][0] <= end){
                end = max(end, intervals[i][1]);//不断更新右区间
                if(i == len - 1)
                    //最后一个区间也合并
                    flag = true;
                //下面的i++同时也改变的for循环里的i值
                i++;//继续合并下一个区间
            }
            //start和end表示Intervals[i-1]的左边界，所以最优intervals[i]区间是否合并了也要标记一下
            result.push_back({start,end});
        }
        //下面考虑的是情况4
        //如果最后一个区间没有合并，将其加入result
        if(flag == false){
            result.push_back({intervals[len - 1][0], intervals[len-1][1]});
        }
        return result;
    }
};

修改数组中的单个数值

//时间复杂度：O(nlogn)，因为有快排
//空间复杂度：O(1),不算result数组（返回值所需容器占的空间）
class Solution {
    static bool cmp(const vector<int>& a, const vector<int>& b){
        return a[0] < b[0];//从小到大
    }
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        //用于返回结果
        vector<vector<int>> result;
        if(intervals.size() == 0)
            return result;
        
        //排序的参数使用了
        sort(intervals.begin(), intervals.end(), cmp);
        //先把第一个数组放入result中，之后遍历其余数组，将这些数组的第一位数与result末尾数组的第二个数对比
        result.push_back(intervals[0]);
        for(int i = 1; i < intervals.size(); i++){
            //result.back()指的是result末尾数组[1]代表是第二个数
            if(result.back()[1] >= intervals[i][0])
                result.back()[1] = max(result.back()[1], intervals[i][1]);
            else
                result.push_back(intervals[i]);
        }
        return result;
    }
};

leetcode738：单调递增的数字

【题目】

给定一个非负整数 N，找出小于或等于 N 的最大的整数，同时这个整数需要满足其各个位数上的数字是单调递增。

（当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时，我们称这个整数是单调递增的。）

示例 1:

输入: N = 10
输出: 9
示例 2:

输入: N = 1234
输出: 1234
示例 3:

输入: N = 332
输出: 299
说明: N 是在 [0, 10^9] 范围内的一个整数。

【思路】

题目要求小于等于N的最大单调递增的整数，那么拿一个两位的数字来举例。

例如：98，一旦出现strNum[i - 1] > strNum[i]的情况（非单调递增），首先想让strNum[i - 1]–，然后strNum[i]给为9，这样这个整数就是89，即小于98的最大的单调递增整数。

这一点如果想清楚了，这道题就好办了。

332->329->299 每一步都是局部最优

局部最优：遇到strNum[i - 1] > strNum[i]的情况，让strNum[i - 1]–，然后strNum[i]给为9，可以保证这两位变成最大单调递增整数。

全局最优：得到小于等于N的最大单调递增的整数。

但这里局部最优推出全局最优，还需要其他条件，即遍历顺序，和标记从哪一位开始统一改成9。

此时是从前向后遍历还是从后向前遍历呢？

从前向后遍历的话，遇到strNum[i - 1] > strNum[i]的情况，让strNum[i - 1]减一，但此时如果strNum[i - 1]减一了，可能又小于strNum[i - 2]。

这么说有点抽象，举个例子，数字：332，从前向后遍历的话，那么就把变成了329，此时2又小于了第一位的3了，真正的结果应该是299。

所以从前后向遍历会改变已经遍历过的结果！

那么从后向前遍历，就可以重复利用上次比较得出的结果了，从后向前遍历332的数值变化为：332 -> 329 -> 299

确定了遍历顺序之后，那么此时局部最优就可以推出全局，找不出反例，试试贪心。

//时间复杂度：O(n)n为数字长度
//空间复杂度：O(n)需要一个字符串，转化为操作符操作更为方便
class Solution {
public:
    int monotoneIncreasingDigits(int N) {
        //将数字N转成字符串
       string strNum = to_string(N);
       //flag用来标记赋值9从哪里开始
       //设置为这个默认值，为了防止第二个for循环在flag没有被赋值的情况之下执行
       int flag = strNum.size();
       for(int i = strNum.size() - 1; i > 0; i--){
           //因为这是大于号所以就把strNum[i-1]=0的情况给省略了
           if(strNum[i-1] > strNum[i]){
               //只要strNum[i-1] > strNum[i] 就将重置标志位，这个标志位可能不断的前移，前一个数要减一
               flag = i;
               strNum[i-1]--;
           }
       }
       //只要高位数字小于地位数字，就把所有的低位数字都置9
       for(int i = flag; i < strNum.size(); i++){
           strNum[i] = '9';
       }
       //将字符串转为数字
       return stoi(strNum);
    }
};

leetcode968：监控二叉树

【题目】

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

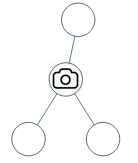
输入：[0,0,null,0,0]
输出：1
解释：如图所示，一台摄像头足以监控所有节点。

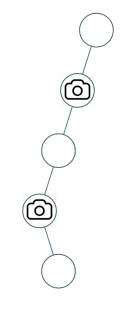
输入：[0,0,null,0,null,0,null,null,0]
输出：2
解释：需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。

提示：

1. 给定树的节点数的范围是 [1, 1000]。
2. 每个节点的值都是 0。

【解题思路】

难点：

1. 需要确定遍历方式
2. 需要状态转移方程

我们之前做动态规划的时候，只要最难的地方在于确定状态转移方程，至于遍历方式无非就是在数组或者二维数组上。

本题并不是动态规划，其本质是贪心，但我们要确定状态转移方式，而且要在树上进行推导，所以难度就上来了，一些同学知道这道题目难，但其实说不上难点究竟在哪。

1. 确定遍历方式

   在安排选择摄像头的位置的时候，我们要从底向上进行推导，因为尽量让叶子节点的父节点安装摄像头，这样摄像头的数量才是最少的。

   如何从底向上推导呢？

   就是后序遍历也就是左右中的顺序，这样就可以从下向上进行推导了。

   int traversal(TreeNode* cur){
       //空节点，该节点有覆盖
       if(终止条件)return;
       
       int left = traversal(cur->left);
       int right = traversal(cur->right);
       
       处理逻辑
       
       return ;
          
   }
   

   代码中我们取了左孩子的返回值，右孩子的返回值，即 left 和 right， 用于推导中间节点的状态

2. 需要状态转移的方程

   几种状态：

   • 该节点有覆盖
   • 本节点有摄像头
   • 本节点有覆盖

   这三个状态用三个数字来表示

   • 0：该节点无覆盖
   • 1：本节点有摄像头
   • 2：本节点有覆盖

【思考】空节点究竟是哪一种状态呢？ 空节点表示无覆盖？ 表示有摄像头？还是有覆盖呢？

理清递推关系：

递推的终止条件应该是遇到空节点，此时应该返回2（有覆盖）。

if(cur == NULL)
	return 2;

递归的函数，以及终止条件已经确定了，再来看看单层逻辑处理

主要有四类情况：

• 情况一：左右节点都有覆盖

  左孩子有覆盖，右孩子右覆盖，那么此时中间节点应该就是无覆盖的状态

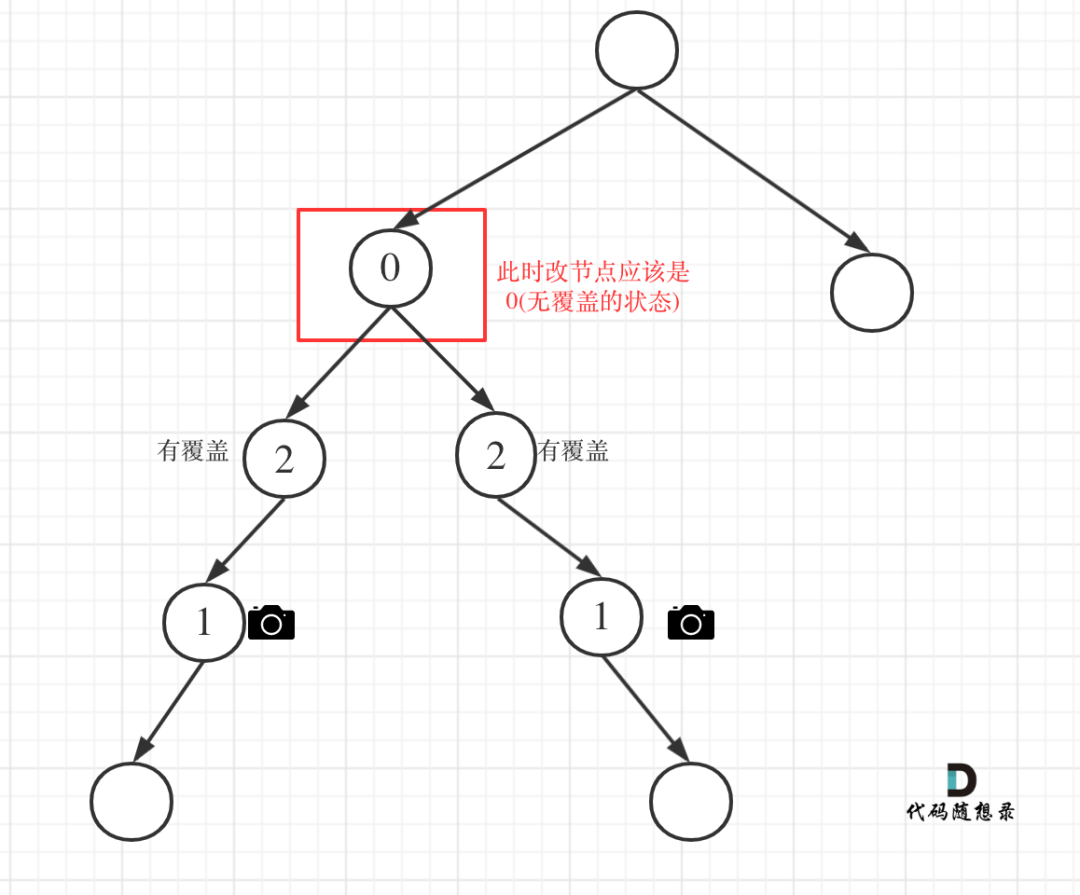
//左右节点都有覆盖
if(left == 2 && right == 2)
	return 0;

• 情况二：左右节点至少有一个无覆盖的情况

  left == 0 && right == 0 左右节点无覆盖
  left == 1 && right == 0 左节点有摄像头，右节点无覆盖
  left == 0 && right == 1 左节点无覆盖，右节点摄像头
  left == 0 && right == 2 左节点无覆盖，右节点覆盖
  left == 2 && right == 0 左节点覆盖，右节点无覆盖

  只要有一个孩子没有覆盖，父节点就应该放摄像头

  if(left == 0 || right == 0){
  	result++;
  	return 1;
  }
  

• 情况三：左右节点至少有一个有摄像头

  如果是以下情况，其实就是 左右孩子节点有一个有摄像头了，那么其父节点就应该是2（覆盖的状态）

  left == 1 && right == 2 左节点有摄像头，右节点有覆盖
  left == 2 && right == 1 左节点有覆盖，右节点有摄像头
  left == 1 && right == 1 左右节点都有摄像头

  if(left == 1 || right == 1)	return 2;
  

• 情况四：头节点没有覆盖

  递归结束之后，可能头结点 还有一个无覆盖的情况，

  

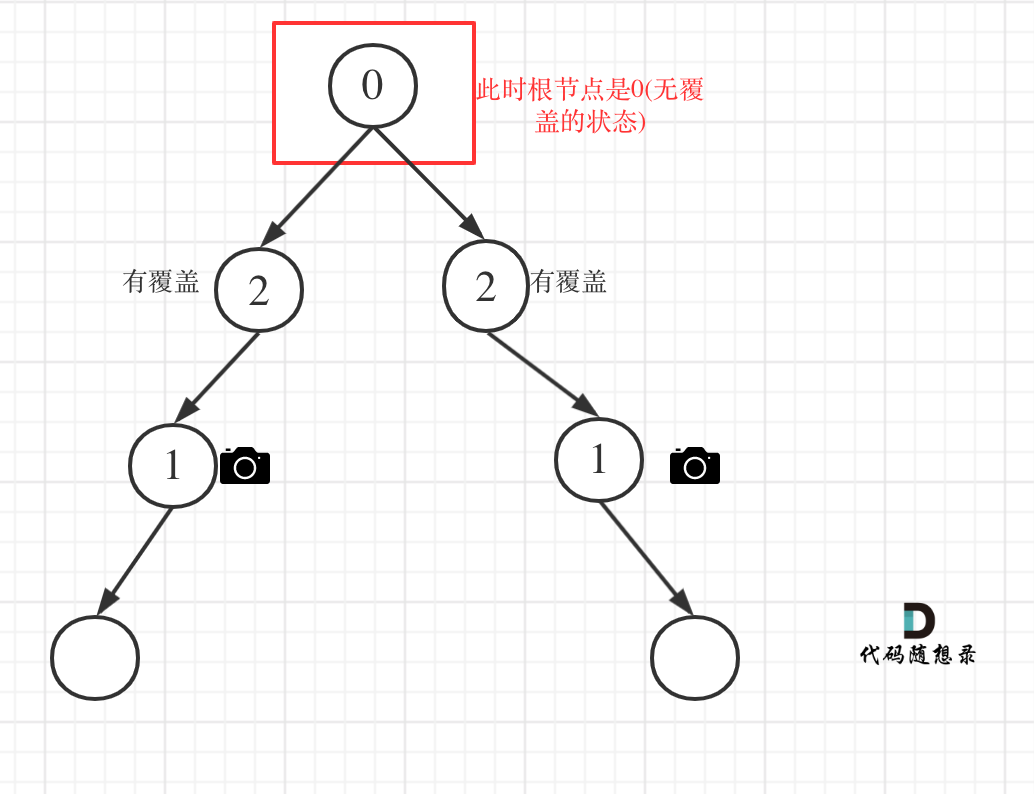
所以递归结束之后，还要判断根节点，如果没有覆盖，result++

int minCameraCover(TreeNode* root) {
    result = 0;
    if (traversal(root) == 0) { // root 无覆盖
        result++;
    }
    return result;
}

[c++代码]

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {

    //用于存储记录摄像头的个数
    int result;
    int traversal(TreeNode* cur){
        //空节点，该节点有覆盖
        if(cur == NULL)
            return 2;
        
        int left = traversal(cur->left);//左
        int right = traversal(cur->right);//右

        /*
            0-》本节点无覆盖
            1-》本节点有摄像头
            2-》本节点有覆盖
        */

        //情况一：
        //左右节点都有覆盖-》左右节点都有覆盖也就是说明左右节点没有摄像头，即该节点没有被覆盖且没有摄像头
        if(left == 2 && right == 2) return 0;

        //情况二：//只要有一个没有覆盖监视到二叉树的就应该增加摄像头的个数，该节点的状态就是有摄像头的状态
        // left == 0 && right == 0 左右节点无覆盖
        // left == 1 && right == 0 左节点有摄像头，右节点无覆盖
        // left == 0 && right == 1 左节点有无覆盖，右节点摄像头
        // left == 0 && right == 2 左节点无覆盖，右节点覆盖
        // left == 2 && right == 0 左节点覆盖，右节点无覆盖
        if(left == 0 || right == 0){
            result++;
            return 1;
        }
        // 情况三
        // left == 1 && right == 2 左节点有摄像头，右节点有覆盖
        // left == 2 && right == 1 左节点有覆盖，右节点有摄像头
        // left == 1 && right == 1 左右节点都有摄像头
        // 其他情况前段代码均已覆盖  
        if(left == 1 || right == 1)
            return 2;

        // 以上代码我没有使用else，主要是为了把各个分支条件展现出来，这样代码有助于读者理解
        // 这个 return -1 逻辑不会走到这里。
        return -1;
    }

public:
    int minCameraCover(TreeNode* root) {
        result = 0;

        //情况四：如果递归结束后，头节点没有被覆盖，则需要一个摄像头覆盖头节点
        if(traversal(root) == 0){
            result++;
        }
        return result;
    }
};

第十章：位运算

对于位运算：一般数字二进制中0或1总和为32个即**（0~31）**

剑指offer15：二进制中1的个数

请实现一个函数，输入一个整数（以二进制串形式），输出该数二进制表示中 1 的个数。例如，把 9 表示成二进制是 1001，有 2 位是 1。因此，如果输入 9，则该函数输出 2。

示例 1：

输入：00000000000000000000000000001011
输出：3
解释：输入的二进制串 00000000000000000000000000001011 中，共有三位为 ‘1’。
示例 2：

输入：00000000000000000000000010000000
输出：1
解释：输入的二进制串 00000000000000000000000010000000 中，共有一位为 ‘1’。
示例 3：

输入：11111111111111111111111111111101
输出：31
解释：输入的二进制串 11111111111111111111111111111101 中，共有 31 位为 ‘1’。

• 输入必须是长度为 32 的 二进制串 。

输入的数据类型uint32_t可以计算，int也可以计算

    class Solution {
    public:
        //问面试官输入要求，如果面试官说时32位二进制，则注意写法是uint32_t (无符号32位)
        int hammingWeight(uint32_t n) {
            int result = 0;
            for(int i = 0; i < 32; i++){
                if((n & (1 << i)) != 0)
                    result++;
            }
            return result;
        }
        //这种方法有一点不好就是改变了n的值
        int hammingWeight(unint32_t n)
        {
            int result = 0;
            for(int i = 0; i < 32; i++)
            {
                if((n >> i) & 1 == 1)
                    result++;
            }
            return result;
        }
    };

leetcode136：只出现一次的数字

【题目】

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

示例 1:

输入: [2,2,1]
输出: 1
示例 2:

输入: [4,1,2,1,2]
输出: 4

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        /*
        //如果用额外的空间来做
        //栈
        stack<int> mystack;
        sort(nums.begin(), nums.end());
        int len = nums.size();
        if(len == 1) return nums[0];
        mystack.push(nums[0]);
        for(int i = 1; i < nums.size(); i++)
        {
            //mystack一定是不能位空的否则不能用top函数
            if(!mystack.empty() && nums[i] == mystack.top()){
                mystack.pop();
            }else{
                mystack.push(nums[i]);
            }
        }
        return mystack.top();*/
		
        //方法二：哈希表来求解
        
        class Solution {
public:
    int singleNumber(vector<int>& nums) {
        unordered_map<int, int> hash_map;
        for(int i = 0; i < nums.size(); i++)
        {
            hash_map[nums[i]]++;
        }
        for(int i = 0; i < nums.size(); i++)
        {
            if(hash_map[nums[i]] == 1)
                return nums[i];
        }
        return -1;
    }
};
        //方法二：位运算
        //X^0 = X
        //X^X = 0;
        int result = 0; 
        int len = nums.size();
        //下面主要逻辑等价于x1 ^ x2 ^ x1 ^ x3 ^ x4 ^ x3 ^x4
        //等价于x1^x1 ^ x2 ^ x3 ^ x3 ^x4 ^ x4
            //这样写默认需求里一定会有单次出现的元素
       for(int i = 0; i < len; i++)
            result ^= nums[i];
            //
        }
        return result;
    }
};

leetcode137：只出现一次数字II

【题目】

给定一个非空整数数组，**除了某个元素只出现一次以外，其余每个元素均出现了三次。**找出那个只出现了一次的元素。

与leetcode136相比，重复出现元素的次数变为奇数次，所以不能直接用依此异或求解。

说明：

你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

示例 1:

输入: [2,2,3,2]
输出: 3
示例 2:

输入: [0,1,0,1,0,1,99]
输出: 99

【代码】

【思考】

对于出现三次的数字，各二进制位出现的次数都是3的倍数。因此，统计所有数字的二进制位中1的出现次数，并对3求余，结果则为只出现一次的次数。

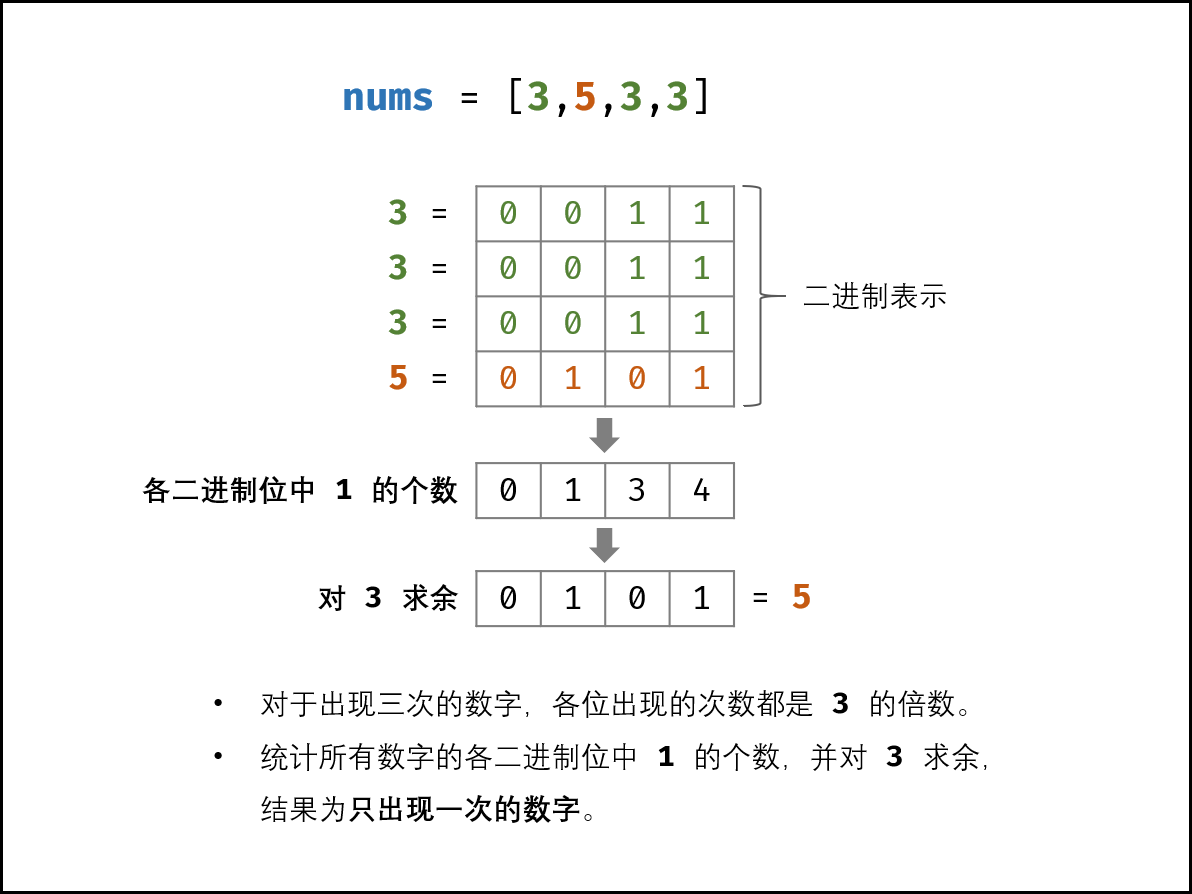
【方法一：遍历统计，效率低】

1. 使用与运算，可获取二进制数字num的最右一位n1：

   n1 = num & i

   ? 配合无符号右移操作，可获取num所有位的值(j即n1~n32)

   num = num >>1;

   建立一个长度为32的数组counts，通过以上方法可记录所有数字的各二进制位的1的出现次数。

2. 将counts各元素对3求余，则结果为“只出现一次的数字”的各二进制位。

   利用左移操作和或运算，可将counts数组中各二进位的值恢复到数字res上(循环区间是i属于[0,31]).

时间复杂度O(N):其中N位数组nums的长度；遍历数组占用O(N),每轮中的常数个位运算操作占用O(1)。
空间复杂度O(1):数组counts长度恒为32，占用常数大小的额外空间。

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        //运用二进制的其它特性；判断整除求余
        /*
        判断所有数字的二进制1的总个数和0的总个数一定有一个不是三的整数倍，如果0不是三的整数倍那么就说明结果的该位二进制位0，否则为1.
        */
        /*
        6       0   1   1   0
        6       0   1   1   0
        6       0   1   1   0
        11      1   0   1   1
        11      1   0   1   1
        11      1   0   1   1
        13      1   1   0   1
        result  4 % 3 = 1
                1   1   0   1
        */       
        int result = 0;
        //遍历列
        for(int i = 0; i < 32; i++){
            int sum = 0;
            //遍历行
            for(int num : nums)
            {
                //求每一列上1的个数
                if(((num >> i) & 1) == 1){
                    sum++;
                }
            }
            if(sum % 3 == 1){
                //  0   0   0   1
                //  0   1   0   0
                //  1   0   0   0
                //等于
                //  1   1   0   1
                //如果余数为1则在i位置上加1
                result += (1 << i);
            }
        }
        return result;
    }
};

【方法二：有限状态自动机】

各二进制位的位运算规则相同，因此只需要考虑一位即可。如下图所示，对于所有数组中的某二进制位1的个数，存在3中状态，即对3余数为0、1、2.

• 若输入二进制位1，则状态按照以下顺序转换；

• 若输入二进制位0，则状态不变。

  0->1->2->0->1…

  

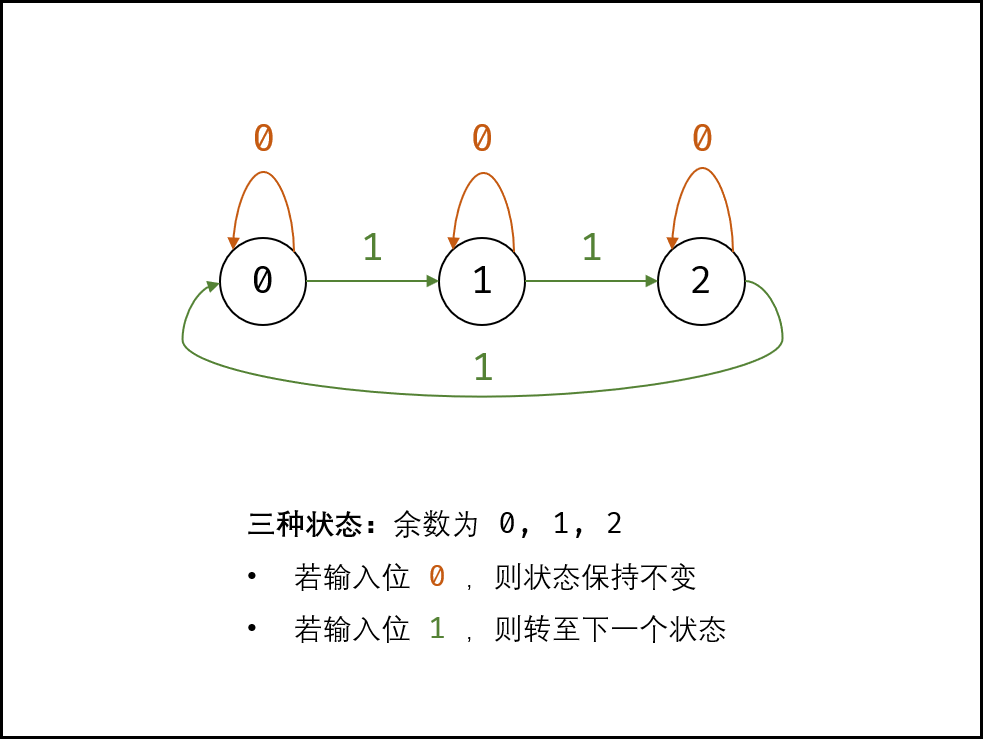
如下图所示，由于二进制只能表示0，1，因此需要使用二进制位来表示3各状态。设此两位分别位two，one。则状态转换变为：

00->01->10->00->…

接下来，需要通过状态转换表导出状态转换的计算公式。首先回忆一下位运算的特点，对于任意二进制位x，有：

• 异或运算：x ^ 0 = x,x ^ 1 = ~x
• 与运算：x & 0 = 0, x & 1 = x

计算one方法：

设当前状态位two one， 此时输入二进制位n。如下图所示，通过对状态表的情况拆分，可推出one的计算方法为：

if two == 0:
	if n == 0:
		one = one
if two == 1:
	one = 0
	

引入异或运算：可将上拆分化简：

if two == 0
	one = one ^ n;
if two ==1 
	one = 0;

引入与运算，

one = one ^ n & ~two;

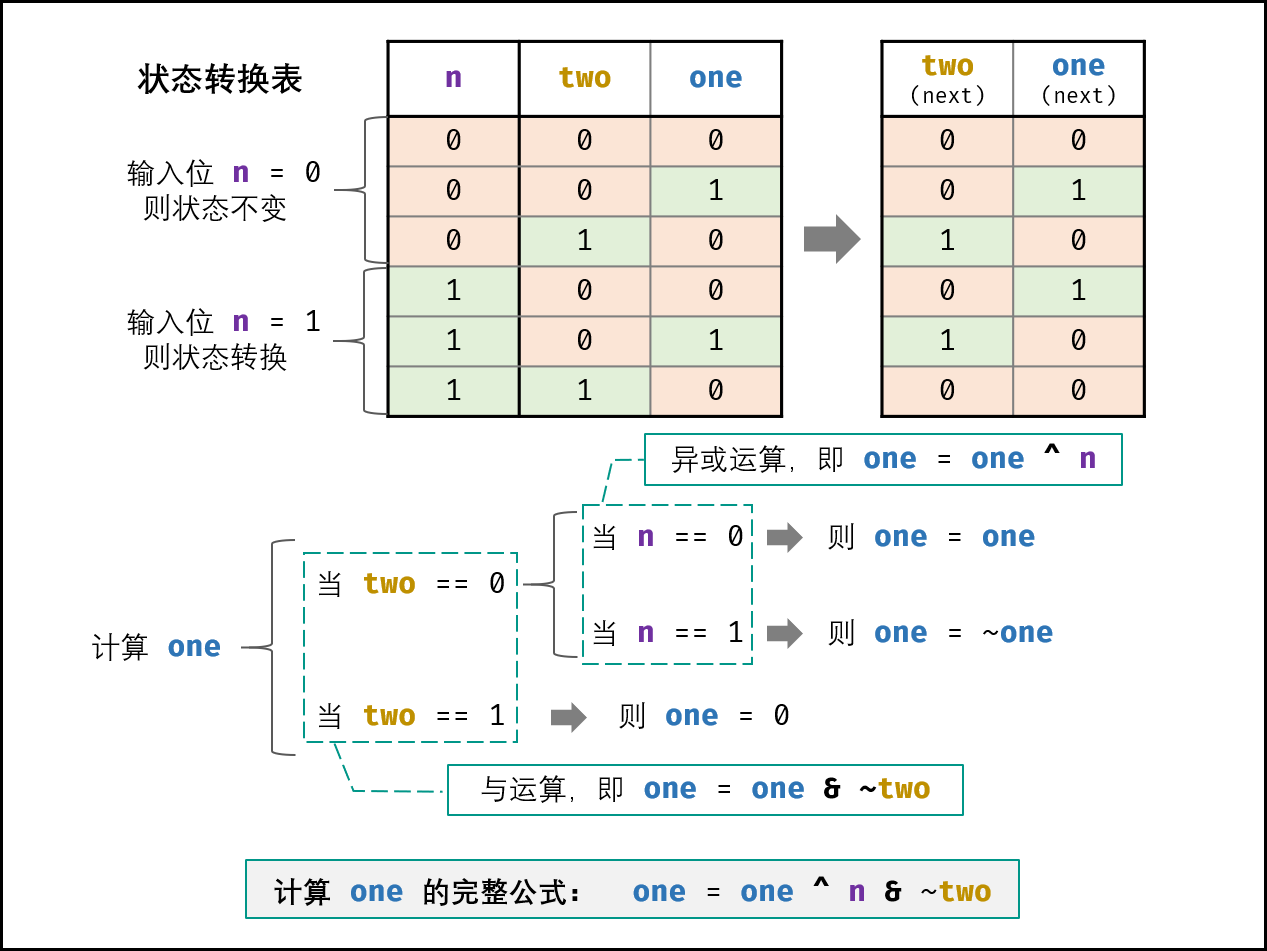
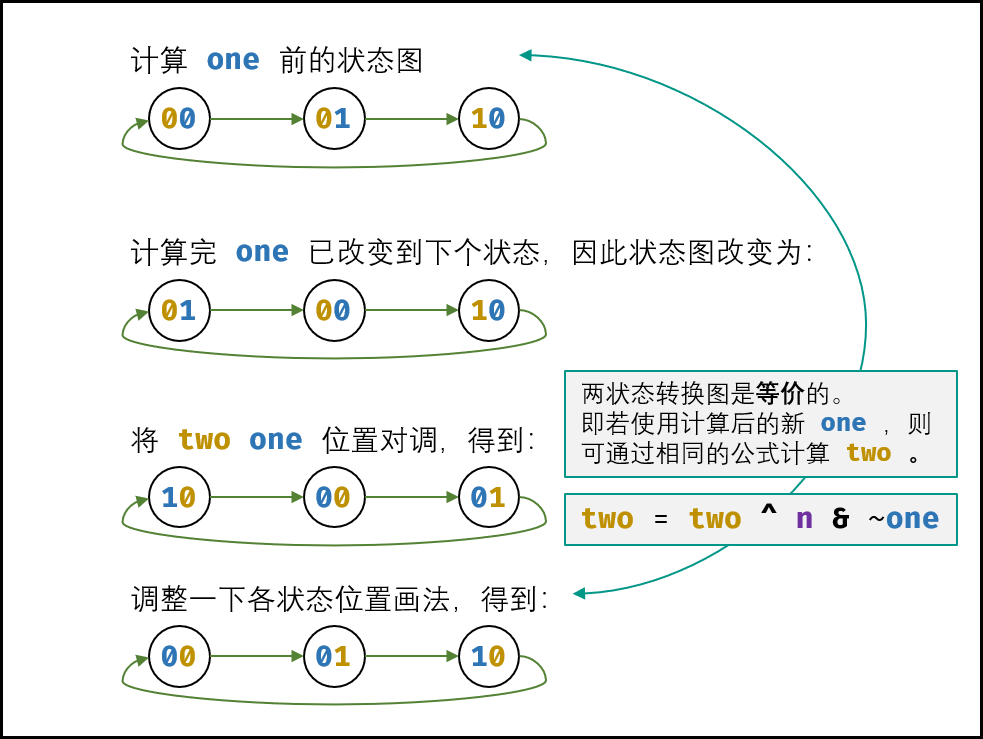
由于是先计算one，因此应在新one的基础上计算two。

如下图所示，修改为新one后，得到了新的状态图。观察发现，可以使用同样的方法计算two，即：

two = two ^ n & ~one

返回值：

以上是对数字二进制中“一位”进行分析，而int类型的其他31位具有相同的运算规则。

遍历完所有数字后，各二进制位都处于状态00和状态01（取决于只出现一次的数字各二进制位是1还是0），而此两状态是由one来记录的(此两状态twos恒为0)，因此返回ones即可。

时间复杂度：O(N),其中N位数组nums的长度；遍历数组占用O(N),每轮中的常数个位运算操作占用O(32*3*2) = O(1)
空间复杂度：O(1)，变量ones，twos使用常数大小的额外空间。

leetcode260：只出现一次数字III

给定一个整数数组 nums，其中恰好有两个元素只出现一次，其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。

进阶：你的算法应该具有线性时间复杂度。你能否仅使用常数空间复杂度来实现？

示例 1：

输入：nums = [1,2,1,3,2,5]
输出：[3,5]
解释：[5, 3] 也是有效的答案。
示例 2：

输入：nums = [-1,0]
输出：[-1,0]
示例 3：

输入：nums = [0,1]
输出：[1,0]
提示：

• 2 <= nums.length <= 3 * 10^4

• -2^31 <= nums[i] <= 2^31 - 1

• 除两个只出现一次的整数外，nums 中的其他数字都出现两次

【思路】

分组异或

对于 两个操作数的每一位，相同结果为0， 不同结果为1。那么再计算过程中，成对出席那的数字的所有位会两两抵消为0，最终得到的结果就是出席那一次的数字。

算法：

• 先对所有数字进行一次异或，得到两个出现一次的数字的异或值。

• 在异或结果中找到任意为 1 的位。

• 根据这一位对所有的数字进行分组。

• 在每个组内进行异或操作，得到两个数字。

class Solution {
public:
    vector<int> singleNumber(vector<int>& nums) {
        /*
        方法一：哈希表
        unordered_map<int, int> hash_map;
        vector<int> result;
        int len = nums.size();
        for(int i = 0; i < len; i++)
        {
            hash_map[nums[i]]++;
        }
        for(int i = 0; i < len; i++)
        {
            if(hash_map[nums[i]] == 1)
                result.push_back(nums[i]);
            if(result.size() == 2)
                break;
        }
        return result;*/
        
        /*
        方法二：栈
        stack<int> mystack;
        vector<int> vec;
        int len = nums.size();
        sort(nums.begin(), nums.end());
        mystack.push(nums[0]);

    
        for(int i = 1;  i < len; i++){
            if(!mystack.empty() && nums[i] == mystack.top()){
                mystack.pop();
            }else{
                mystack.push(nums[i]);
            }
        }

        while(!mystack.empty()){
            vec.push_back(mystack.top());
            mystack.pop();
        }
        return {vec.begin(), vec.end()};
        */
        //方法三：位运算
        int res = 0;
        int num1 = 0, num2 = 0;
        //对所有数字进行异或
        for(int num : nums)
        {
            res ^= num;
        }
        int a = 1;
        //再异或值中找到为1的位
        while((res & a) == 0)
        {
            a <<= 1;//h移动后的值要赋值给h所以是<<=
        }
        //分组异或
        for(int num : nums)
        {
            //某位置为1与某位置为0，分为两个组；对两个组内分别异或
            if((a & num) == 0)//这一定是与0进行比较，因为如果h & num 不一定等于1，可以是非零任意数
               num1 ^= num;
            else
               num2 ^= num;
        }
        return{num1, num2};
    }
};

leetcode201:数字范围按位与

给你两个整数 left 和 right ，表示区间 [left, right] ，返回此区间内所有数字 按位与 的结果（包含 left 、right 端点）。

示例 1：

输入：left = 5, right = 7
输出：4
示例 2：

输入：left = 0, right = 0
输出：0
示例 3：

输入：left = 1, right = 2147483647
输出：0

提示：

0 <= left <= right <= 2^31 - 1

【思路】

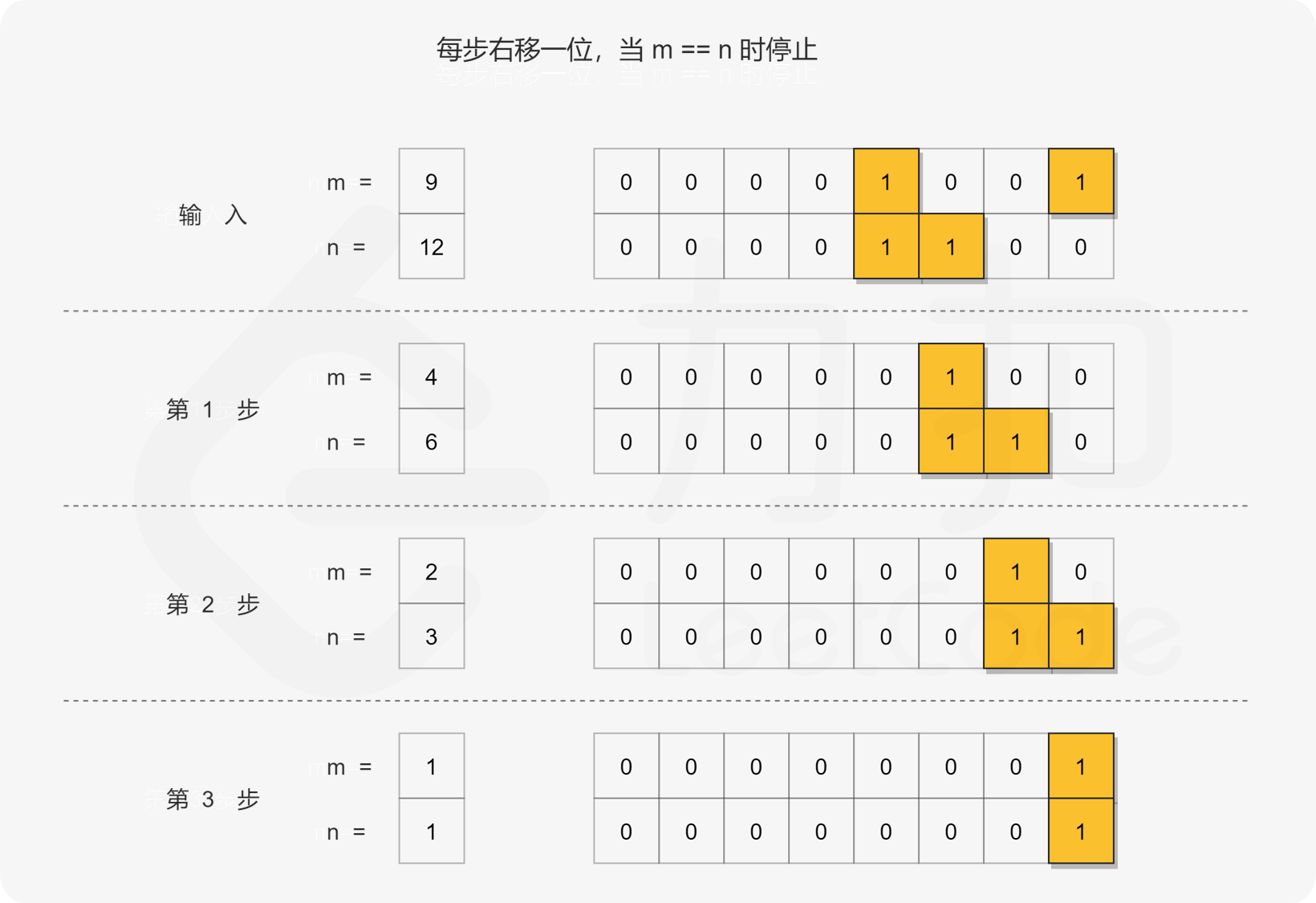
算法：

• 通过右移，将两个数字压缩为它们的公共前缀，在迭代过程中，我们计算向右移动的次数
• 得到公共前缀左移相同的操作数得到结果

class Solution {
public:
    int rangeBitwiseAnd(int left, int right) {
        /*
        //这种方法超时
        int result = left;
        while(right >= (left + 1))
        {
            result &= left + 1;
            left++;
        }
        return result;
        */
        //遍历列呢
        int move_times = 0;
        while(left != right)
        {
            left = left >> 1;
            right = right >> 1;
            move_times++;
        }
        return left << move_times;//易错这里并不是return 1 << move_times因为left可能位0
    
    	//Brian Kernighan算法
        /*
        该算法用于清除二进制串中最右边的1.Brian Kernighan算法的关键在于我们每次对number和number-1之间按位运算后，number中最右边的1会被抹去变成0
        */
        时间复杂度：O(log n)
        空间复杂度:O(1)
         while(left < right)
        {
            right = right & (right - 1);
        }
        return right;
    
    }
};

leetcode461：汉明距离

两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。

给出两个整数 x 和 y，计算它们之间的汉明距离。

注意：
0 ≤ x, y < 2^31.

示例:

输入: x = 1, y = 4

输出: 2

解释:
1   (0 0 0 1)
4   (0 1 0 0)
       ↑   ↑

上面的箭头指出了对应二进制位不同的位置。

class Solution {
public:
    int hammingDistance(int x, int y) {
        /*
        int a = 1;
        int result = 0;
        //为什么i从0到32是因为数据量
        for(int i = 0; i < 32; i++)
        {
            a = 1 << i;//a的位置必须在if的上面
            /*
            逻辑：
            1000
            0001
            -------
            1+0+0+1 = 2
           
            if(((x & a) ^ (y & a)) != 0)
                result++;
        }
        return result;
         */
         int temp = x ^ y;
         int distance = 0;
         while(temp != 0)
         {
             distance += 1;
             /*
             布莱恩尼克根算法：
             */
             temp = temp & (temp - 1);
         }
         return distance;
    }
};

leetcode447：汉明距离总和

【题目】

两个整数的 汉明距离 指的是这两个数字的二进制数对应位不同的数量。

计算一个数组中，任意两个数之间汉明距离的总和。

示例:

输入: 4, 14, 2

输出: 6

解释: 在二进制表示中，4表示为0100，14表示为1110，2表示为0010。（这样表示是为了体现后四位之间关系）
所以答案为：
HammingDistance(4, 14) + HammingDistance(4, 2) + HammingDistance(14, 2) = 2 + 2 + 2 = 6.
注意:

数组中元素的范围为从 0到 10^9。
数组的长度不超过 10^4。

【分析】

每一位的汉明距离 = 该位1的个数 * 该位0的个数。
因为数据量是10^9 < 2^31所以该数可以用32位表示

class Solution {
    
public:
    int totalHammingDistance(vector<int>& nums) {
        unsigned int a = 1, num_one = 0;
        int res = 0;
        for(int i = 0; i < 32; i++)
        {
            for(auto num : nums)
            {
                if((num & a) == a)
                {
                    num_one++;
                }
            }
            res += num_one * (nums.size() - num_one);
            num_one = 0;
            a = a << 1;
        }
        return res;
    }
};

leetcode1486：数组异或操作

给你两个整数，n 和 start 。

数组 nums 定义为：nums[i] = start + 2*i（下标从 0 开始）且 n == nums.length 。

请返回 nums 中所有元素按位异或（XOR）后得到的结果。

示例 1：

输入：n = 5, start = 0
输出：8
解释：数组 nums 为 [0, 2, 4, 6, 8]，其中 (0 ^ 2 ^ 4 ^ 6 ^ 8) = 8 。
“^” 为按位异或 XOR 运算符。
示例 2：

输入：n = 4, start = 3
输出：8
解释：数组 nums 为 [3, 5, 7, 9]，其中 (3 ^ 5 ^ 7 ^ 9) = 8.
示例 3：

输入：n = 1, start = 7
输出：7
示例 4：

输入：n = 10, start = 5
输出：2

提示：

1 <= n <= 1000
0 <= start <= 1000
n == nums.length

class Solution {
public:
    int xorOperation(int n, int start) {
        //确定数据量与数据局限：n大于1小于1000；start大于0小于1000
        if(n == 1)
            return start;
        long long temp = start;
        int res = 0;
        int loop = n;
        while(loop)
        {
            res ^= temp;
            temp = temp + 2;
            loop--;
        }
        return res;
    }
};

leetcode389：找不同

给定两个字符串 s 和 t，它们只包含小写字母。

字符串 *t* 由字符串 *s* 随机重排，然后在随机位置添加一个字母。

请找出在 t 中被添加的字母。

示例 1：

输入：s = “abcd”, t = “abcde”
输出：“e”
解释：‘e’ 是那个被添加的字母。
示例 2：

输入：s = “”, t = “y”
输出：“y”
示例 3：

输入：s = “a”, t = “aa”
输出：“a”
示例 4：

输入：s = “ae”, t = “aea”
输出：“a”

提示：

0 <= s.length <= 1000
t.length == s.length + 1
s 和 t 只包含小写字母

class Solution {
public:
    char findTheDifference(string s, string t) {
        char res = 0;
        for(int i =  0; i < s.size(); i++)
        {
            res ^= s[i];
        }
        for(int i = 0; i < t.size(); i++)
        {
            res ^= t[i];
        }
        return res;
    }
};

class Solution {
public:
    char findTheDifference(string s, string t) {
        unordered_map<char, int> Hash_map1;
        unordered_map<char, int> Hash_map2;
        
        for(int i = 0; i < t.size(); i++)
        {
           Hash_map1[t[i]]++;
        }
        for(int i = 0; i < s.size(); i++)
        {
            Hash_map1[s[i]]--;
        }
        for(auto iter = Hash_map1.begin(); iter != Hash_map1.end(); iter++)
        {
            if(iter->second == 1)
                return iter->first;
        }
        return ' ';
    }
};

leetcode1734：解码异或后的排列

给你一个**【输出数据的特点】**整数数组 perm ，它是前 n 个正整数的排列，且 n 是个 奇数 。

它被加密成另一个长度为 n - 1 的整数数组 encoded ，满足 encoded[i] = perm[i] XOR perm[i + 1] 。比方说，如果 perm = [1,3,2] ，那么 encoded = [2,1] 。

给你 encoded 数组，请你返回原始数组 perm 。题目保证答案存在且唯一。

示例 1：

输入：encoded = [3,1]
输出：[1,2,3]
解释：如果 perm = [1,2,3] ，那么 encoded = [1 XOR 2,2 XOR 3] = [3,1]
示例 2：

输入：encoded = [6,5,4,6]
输出：[2,4,1,5,3]

提示：

3 <= n < 10^5
n 是奇数。
encoded.length == n - 1

class Solution {
public:
    vector<int> decode(vector<int>& encoded) {
        //第一步需要求出perm[0]的元素
        //prem[0]^[除了首元素的异或，用到了n是奇数的条件] = TOTAL[用到了n是正整数排列的条件]
        int Odd = 0;
        int Total = 0;
        int len = encoded.size();
        for(int i = 1; i < len; i = i + 2)
        {
            Odd ^= encoded[i]; 
        } 
        for(int i = 1; i <= len + 1; i++)
        {
            Total ^= i;
        }
        
        vector<int> prem(len + 1);
        prem[0] = Total ^ Odd;
        for(int i = 1; i < len + 1; i++)
        {
            prem[i] = encoded[i-1]^prem[i-1];
        }
        return prem;
    }
};

leetcode1310：子数组异或查询

有一个正整数数组 arr，现给你一个对应的查询数组 queries，其中 queries[i] = [Li, Ri]。

对于每个查询 i，请你计算从 Li 到 Ri 的 XOR 值（即 arr[Li] xor arr[Li+1] xor … xor arr[Ri]）作为本次查询的结果。

并返回一个包含给定查询 queries 所有结果的数组。

示例 1：

输入：arr = [1,3,4,8], queries = [[0,1],[1,2],[0,3],[3,3]]
输出：[2,7,14,8]
解释：
数组中元素的二进制表示形式是：
1 = 0001
3 = 0011
4 = 0100
8 = 1000
查询的 XOR 值为：
[0,1] = 1 xor 3 = 2
[1,2] = 3 xor 4 = 7
[0,3] = 1 xor 3 xor 4 xor 8 = 14
[3,3] = 8
示例 2：

输入：arr = [4,8,2,10], queries = [[2,3],[1,3],[0,0],[0,3]]
输出：[8,0,4,4]

提示：

1 <= arr.length <= 3 * 10^4
1 <= arr[i] <= 10^9
1 <= queries.length <= 3 * 10^4
queries[i].length == 2
0 <= queries[i] [0] <= queries[i] [1] < arr.length

【思路】

这种方法是前缀后缀查询

class Solution {
public:
    vector<int> xorQueries(vector<int>& arr, vector<vector<int>>& queries) {
        /*
         vector<int> res;
         int a = 6 ^ 14;
        cout<< a <<endl;
        for(int i = 0; i < queries.size(); i++)
        {
            int num1 = queries[i][0];
            int num2 = queries[i][1];
            int temp = 0;
            for(int j = num1; j <= num2; j++)
            {
                temp ^= arr[j];
            }
            res.push_back(temp);
        }
        return res;*/
        //创建一个数组用于存储从0~arr.size()的值
        int len = arr.size();
        vector<int> Xor_Vec(len + 1, 0);
        vector<int> res;
        for(int i = 1; i < len + 1; i++)
        {
            Xor_Vec[i] = Xor_Vec[i-1] ^ arr[i-1];
        }
        for(int i = 0; i < queries.size(); i++)
        {
            int num1 = queries[i][0];
            int num2 = queries[i][1];
            res.push_back(Xor_Vec[num1] ^ Xor_Vec[num2+1]);
        }
        return res;
    }
};

leetcode1442：形成两个异或相等数组的三元数组（前缀和的使用）

如果求部分和就需要使用前缀和技巧了

给你一个整数数组 arr 。

现需要从数组中取三个下标 i、j 和 k ，其中 (0 <= i < j <= k < arr.length) 。

a 和 b 定义如下：

a = arr[i] ^ arr[i + 1] ^ ... ^ arr[j - 1]
b = arr[j] ^ arr[j + 1] ^ ... ^ arr[k]
注意：^ 表示 按位异或 操作。

请返回能够令 a == b 成立的三元组 (i, j , k) 的数目。

 

示例 1：

输入：arr = [2,3,1,6,7]
输出：4
解释：满足题意的三元组分别是 (0,1,2), (0,2,2), (2,3,4) 以及 (2,4,4)
示例 2：

输入：arr = [1,1,1,1,1]
输出：10
示例 3：

输入：arr = [2,3]
输出：0
示例 4：

输入：arr = [1,3,5,7,9]
输出：3
示例 5：

输入：arr = [7,11,12,9,5,2,7,17,22]
输出：8
 

提示：

1 <= arr.length <= 300
1 <= arr[i] <= 10^8

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/count-triplets-that-can-form-two-arrays-of-equal-xor
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

【思路】

方法一：最直观暴力法

首先进行三重循环分别确定i，j，k值，然后计算其arr[i]_{arr[j-1]与arr[j]}arr[k]的异或值；时间复杂度：O(n^4);空间复杂度：O(1)

结果超时

class Solution {
public:
    int countTriplets(vector<int>& arr) {
        int n = arr.size(), ans = 0;
        for(int i = 0; i < n; ++i)
        {
            for(int j = i+1; j < n; ++j)
            {
                for(int k = j; k < n; ++k)
                {
                    int a = 0, b = 0;
                    for(int x = i; x < j; ++x)
                        a ^= arr[x];
                    for(int y = j; y <= k; ++y)
                        b ^= arr[y];
                    ans += (a == b);
                }
            }
        }
        return ans;
    }
};

方法二：暴力解法优化（前缀项处理）

a = arr[i] - arr[j-1];

b = arr[j] - arr[k];

从方法一中看到的问题就是计算其a与b都需要两层for循环，这样时间消耗是巨大的。优化的方向就是避免使用遍历的方法来计算区间的异或值-----》解决的办法就是前缀异或数组

异或有自反性： 即任何数异或其本身等于 0；
比如： a ⊕ a = 0;
前缀异或的解释：对于 preXOR[i] 表示为前 i 项数的异或值
假设我们有数组 arr: [1, 2, 3, 4, 7, 9]; 
前零项的异或值为: 0 = 0
前一项的异或值为: 1 = 1
前二项的异或值为: 1 ⊕ 2 = 3
前三项的异或值为: 1 ⊕ 2 ⊕ 3 = 0
前四项的异或值为: 1 ⊕ 2 ⊕ 3 ⊕ 4 = 4
前五项的异或值为: 1 ⊕ 2 ⊕ 3 ⊕ 4 ⊕ 7 = 3
前六项的异或值为: 1 ⊕ 2 ⊕ 3 ⊕ 4 ⊕ 7 ⊕ 9 = 10

因此它的前缀异或数组为 preXOR: [0, 1, 3, 0, 4, 3, 10];

假设现在我们想求第 3 项到第 6 项的异或值， 此时我们不需要去暴力计算 "3 ⊕ 4 ⊕ 7 ⊕ 9"
我们知道 (3 ⊕ 4 ⊕ 7 ⊕ 9) = (1 ⊕ 2) ⊕ (1 ⊕ 2 ⊕ 3 ⊕ 4 ⊕ 7 ⊕ 9) 
我们可以使用前缀异或的数组来计算第 3 项到第 6 项的异或值
(1 ⊕ 2) 为前 2 项的异或值为 “3”
(1 ⊕ 2 ⊕ 3 ⊕ 4 ⊕ 7 ⊕ 9) 为前 6 项异或值为 “10”
因此第 3 项到第 6 项的异或值为：3 ⊕ 10 = 9
所有对于前缀异或我们同样也可以用O(1)的时间计算区间内的异或值

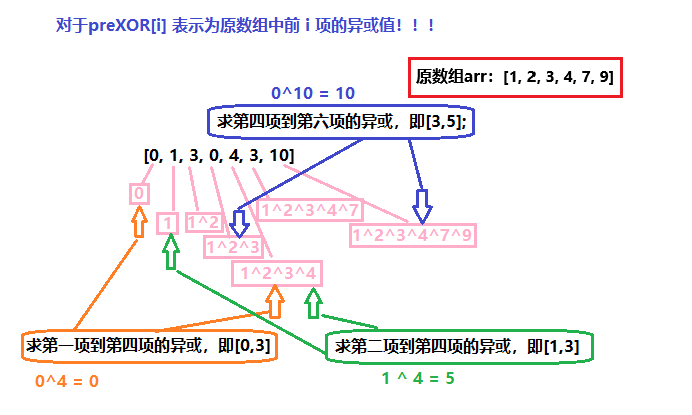
相比较方法一来说，计算a与b的值我们就可以从O(n)降到O(1).只要想到前缀和数组其实就已经能解决此问题了

时间复杂度：O(n^3)

空间复杂度：O(n)，异或数组所占用的空间

class Solution {
public:
    int countTriplets(vector<int>& arr) {
        int n = arr.size(), ans = 0;
        vector<int> preXor(n+1);
        for(int i = 0; i < n; ++i)
            preXor[i+1] = preXor[i]^arr[i];
        for(int i = 1; i <= n; ++i)
        {
            for(int j = i+1; j <= n; ++j)
            {
                for(int k = j; k <= n; ++k)
                {
                    int a = preXor[j-1]^preXor[i-1];
                    int b = preXor[k]^preXor[j-1];
                    ans += (a == b);
                }
            }
        }
        return ans;
    }
};

【方法三：利用异或的性质】这方法也太香了

a = arr[i] - arr[j-1]

b = arr[j] - arr[k]

a ⊕ a = 0,由于此题目让我们找到满足a==b的坐标，那么当a=b时需要满足什么条件，有a ⊕ b = 0所以我们可以得到arr[i] ^… arr[j-1]^ arr[j] ^… arr[k] = 0。因此在i之前的前缀异或值到k时不会变。所以在区间[i, k]内，j在哪里并不重要，因为无论j在哪里，i到k的异或值都等于0.

时间复杂度：O(n^2)

空间复杂度：O(n)异或数组所占用的空间

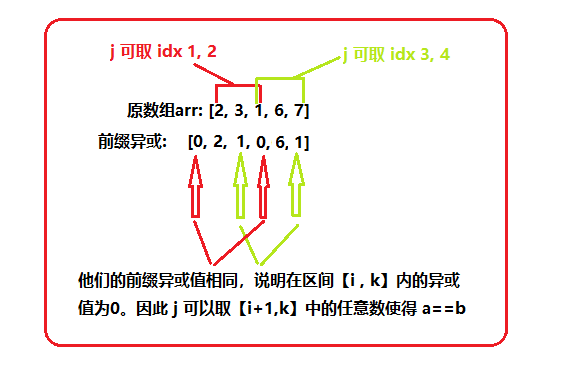
class Solution {
public:
    int countTriplets(vector<int>& arr) {
        //n为数组的长度，ans为结果
        int n = arr.size(), ans = 0;
        vector<int> preXor(n+1);
        //求解前缀和
        for(int i = 0; i < n; ++i)
            preXor[i+1] = preXor[i]^arr[i];
        //计算ans，只需要求i与k就可以了
        for(int i = 1; i <= n; ++i)
            for(int k = i+1; k <= n; ++k)
                //为什么这里时preXor[i-1]
                if(preXor[i-1] == preXor[k])
                    //为什么这里时k-i
                    ans += k-i;
        return ans;
    }
};

leetcode？？？你能在你最喜欢的那天吃到你最喜欢的糖果吗？【数组前缀和】

【题目】

给你一个下标从 0 开始的正整数数组 candiesCount ，其中 candiesCount[i] 表示你拥有的第 i 类糖果的数目。同时给你一个二维数组 queries ，其中 queries[i] = [favoriteTypei, favoriteDayi, dailyCapi] 。

你按照如下规则进行一场游戏：

你从第 0 天开始吃糖果。
你在吃完 所有 第 i - 1 类糖果之前，不能 吃任何一颗第 i 类糖果。
在吃完所有糖果之前，你必须每天 至少 吃 一颗 糖果。
请你构建一个布尔型数组 answer ，满足 answer.length == queries.length 。answer[i] 为 true 的条件是：在每天吃 不超过 dailyCapi 颗糖果的前提下，你可以在第 favoriteDayi 天吃到第 favoriteTypei 类糖果；否则 answer[i] 为 false 。注意，只要满足上面 3 条规则中的第二条规则，你就可以在同一天吃不同类型的糖果。

请你返回得到的数组 answer 。

 

示例 1：

输入：candiesCount = [7,4,5,3,8], queries = [[0,2,2],[4,2,4],[2,13,1000000000]]
输出：[true,false,true]
提示：
1- 在第 0 天吃 2 颗糖果(类型 0），第 1 天吃 2 颗糖果（类型 0），第 2 天你可以吃到类型 0 的糖果。
2- 每天你最多吃 4 颗糖果。即使第 0 天吃 4 颗糖果（类型 0），第 1 天吃 4 颗糖果（类型 0 和类型 1），你也没办法在第 2 天吃到类型 4 的糖果。换言之，你没法在每天吃 4 颗糖果的限制下在第 2 天吃到第 4 类糖果。
3- 如果你每天吃 1 颗糖果，你可以在第 13 天吃到类型 2 的糖果。
示例 2：

输入：candiesCount = [5,2,6,4,1], queries = [[3,1,2],[4,10,3],[3,10,100],[4,100,30],[1,3,1]]
输出：[false,true,true,false,false]
 

提示：

1 <= candiesCount.length <= 10^5
1 <= candiesCount[i] <= 10^5
1 <= queries.length <= 10^5
queries[i].length == 3
0 <= favoriteTypei < candiesCount.length
0 <= favoriteDayi <= 10^9
1 <= dailyCapi <= 10^9

【解题思路】

题目中的小陷阱：我们是从第0天开始吃糖果。因此对于第i各询问，我们可以吃favoriteDay+1天的糖果。

【思路与算法】

对于第i个询问(favoriteType，favoriteDay，dailyCap),我们每天至少吃1颗糖，至多吃dailyCap颗糖果，因此我们吃糖果的数量落入的区间：

【favoriteDay+1, (favoriteDay+1)*dailyCap】

内。那么只要这个区间包含一颗第favoriteType种类型的糖果，就可以满足要求了。

因此我们求出糖果数量的前缀和，记录在数组sum种，那么第favoriteType种类型的糖果对应的编号范围为：

【sum[favoiteType-1], sum[favoriteType]】

特别地，如果favoriteType为0，那么区间的左端点为1.

我们只要判断这两个区间是否有交集即可，如果有交集，说明我们可以吃到difavoriteType类的糖果。判断是否有交集的方法如下：

对于区间[x1,y1]以及[x2,y2],它们没有交集当且仅当x1>y2或者y1<x2

复杂度分析：
	时间复杂度：O(n+q),其中n和q分别是数组candiesCount和queries的长度。我们需要O(n)的时间计算前缀和，O(q)的时间得到所有询问的结果
	空间复杂度：O(n),即为存储前缀和数组需要的空间。注意返回值不计入空间复杂度

class Solution {
    using LL = long long;//数据类型都转为long long
public:
    vector<bool> canEat(vector<int>& candiesCount, vector<vector<int>>& queries) {
        int n = candiesCount.size();
        vector<LL> sum(n);
        sum[0] = candiesCount[0];
        for(int i = 1; i < n; i++)
        {
            sum[i] = sum[i-1] + candiesCount[i];
        }

        vector<bool> res;
        for(const auto & q : queries)
        {
            int favoriteType = q[0], favoriteDay = q[1], dailyCap = q[2];
            LL x1 = favoriteDay + 1;
            LL y1 = (LL)(favoriteDay + 1) * dailyCap;//如果不是longlong 这里可能会越界
            LL x2 = favoriteType == 0? 1 : sum[favoriteType - 1] + 1;//注意x2的取值，[x2, y2]是喜欢糖果在的区间
            LL y2 = sum[favoriteType];

            res .push_back(!(x1 > y2 || y1 < x2));//喜欢糖果区间与需求糖果区间有交集
        }
        return res;
    }
};

leetcode523：连续的子数组和【前缀和思想】

【题目】

给你一个整数数组 nums 和一个整数 k ，编写一个函数来判断该数组是否含有同时满足下述条件的连续子数组：

1. 子数组大小 至少为 2 ，且
2. 子数组元素总和为 k 的倍数。
如果存在，返回 true ；否则，返回 false 。

如果存在一个整数 n ，令整数 x 符合 x = n * k ，则称 x 是 k 的一个倍数。

示例 1：

输入：nums = [23,2,4,6,7], k = 6
输出：true
解释：[2,4] 是一个大小为 2 的子数组，并且和为 6 。
示例 2：

输入：nums = [23,2,6,4,7], k = 6
输出：true
解释：[23, 2, 6, 4, 7] 是大小为 5 的子数组，并且和为 42 。 
42 是 6 的倍数，因为 42 = 7 * 6 且 7 是一个整数。
示例 3：

输入：nums = [23,2,6,4,7], k = 13
输出：false
 

提示：

1 <= nums.length <= 10^5
0 <= nums[i] <= 10^9
0 <= sum(nums[i]) <= 2^31 - 1
1 <= k <= 2^31 - 1

【代码：前缀和+哈希表】

/*
子数组的和本质其实就是两个前缀和的差值，而差值等于n*k,那么意味着这两个前缀和%k是一样的；
我们可以用一个map来记录(前缀和%k)到对应位置的映射
一旦发现当前前缀和%k已经在map里保存，而且两者序号差距大于等于2就返回成功

坑：
需要考虑当前前缀和本身就可以被k整除，增加初始化0~-1的映射，这样子保证如1-（-1）=2>=2这个条件
考虑k=0的情况
*/

class Solution {
public:
    bool checkSubarraySum(vector<int>& nums, int k) {
        int n = nums.size();
        unordered_map<int, int> sum2index;
        //考虑能被k整除的特殊情况
        sum2index[0] = -1;

        int sum = 0;
        for(int i = 0; i < n; i++)
        {
            sum += nums[i];
            if(k != 0)
            {
                sum %= k;
            }
            //下面两个if不可以合并一起写
            if(sum2index.find(sum) == sum2index.end())
            {
                sum2index[sum] = i;
            }
            //发现至少有两个数的子数组
            else if(i - sum2index[sum] >= 2)
                return true;
        }
        //都找不到则返回失败
        return false;
    }
};

leetcode525.连续数组

【题目】

给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组，并返回该子数组的长度。
示例 1:

输入: nums = [0,1]
输出: 2
说明: [0, 1] 是具有相同数量0和1的最长连续子数组。
示例 2:

输入: nums = [0,1,0]
输出: 2
说明: [0, 1] (或 [1, 0]) 是具有相同数量0和1的最长连续子数组。
 

提示：

1 <= nums.length <= 10^5
nums[i] 不是 0 就是 1

【解题思路】

与523相同

算法步骤：

1. 创建一个哈希表，用key来存储cur值，value来存储当前index
2. 假设我们碰到0就将cur decrement（减一），碰到1则increment(加一)。
3. 如果我们能在哈希表中找到当前的cur值，则取出对应的pos，在看当前的index-cur是否比ans大，取其中的最优解。

核心思想：

由于碰上1加一，碰0减一的操作，当0与1数量一致时（连续数组），其连续数组的和为零。因此我们直到数组前面的cur值是什么，在到达该连续数组尾部时不会变。因此我们只需要坚持哈希表中是否存在其相同的cur值即可！

1. 为什么在哈希表中找到了相同的cur值算找到了一串连续数组？

   

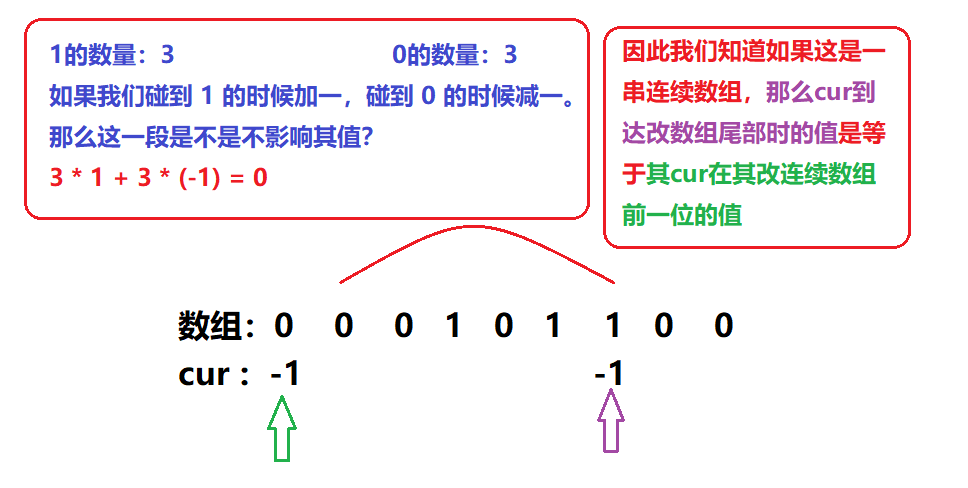
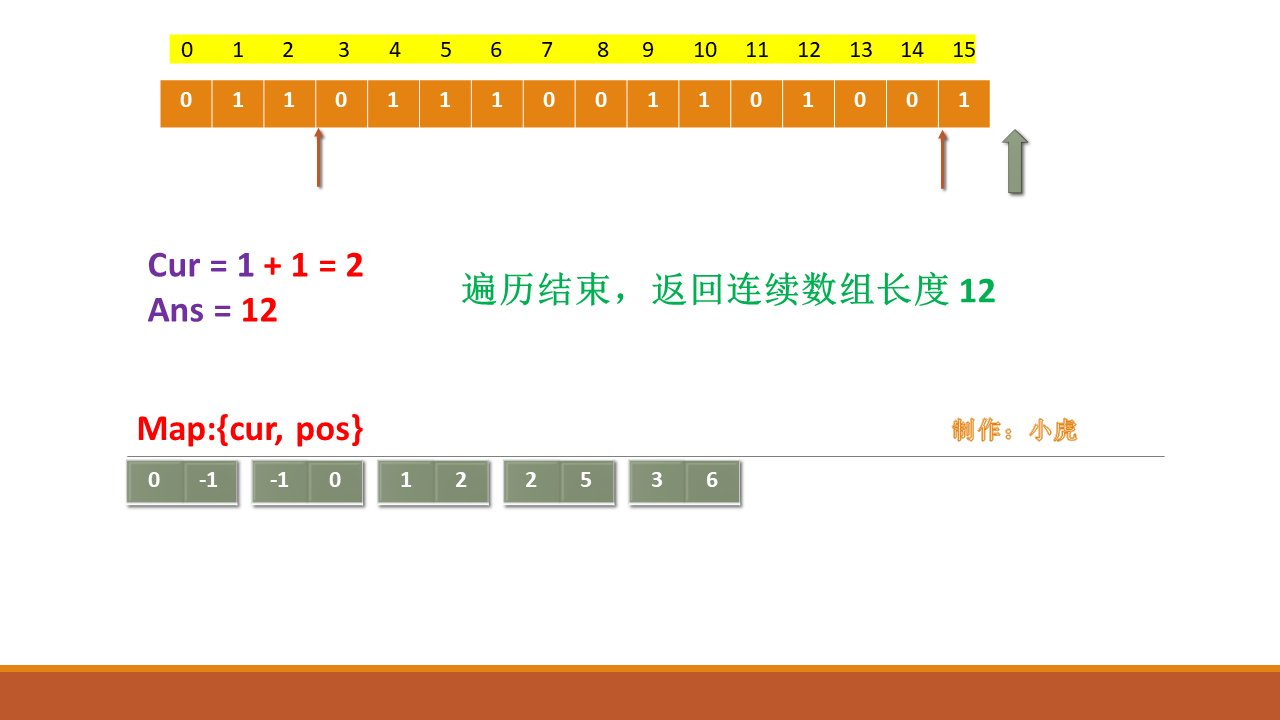
2. 为什么要在哈希表中插入{0,1}?

   这是为了辅助讨论数组的起点index==0的位置情况，如果最长连续数组在数组的最前方，不插入{0,1}会得到错误的答案，因此我们一定要插入该辅助键值！

   

leetcode1738：找出第K大的异或坐标值

【题目】

给你一个二维矩阵 matrix 和一个整数 k ，矩阵大小为 m x n 由非负整数组成。

矩阵中坐标 (a, b) 的 值 可由对所有满足 0 <= i <= a < m 且 0 <= j <= b < n 的元素 matrix[i][j]（下标从 0 开始计数）执行异或运算得到。

请你找出 matrix 的所有坐标中第 k 大的值（k 的值从 1 开始计数）。

示例 1：

输入：matrix = [[5,2],[1,6]], k = 1
输出：7
解释：坐标 (0,1) 的值是 5 XOR 2 = 7 ，为最大的值。
示例 2：

输入：matrix = [[5,2],[1,6]], k = 2
输出：5
解释：坐标 (0,0) 的值是 5 = 5 ，为第 2 大的值。
示例 3：

输入：matrix = [[5,2],[1,6]], k = 3
输出：4
解释：坐标 (1,0) 的值是 5 XOR 1 = 4 ，为第 3 大的值。
示例 4：

输入：matrix = [[5,2],[1,6]], k = 4
输出：0
解释：坐标 (1,1) 的值是 5 XOR 2 XOR 1 XOR 6 = 0 ，为第 4 大的值。

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 1000
0 <= matrix[i][j] <= 106
1 <= k <= m * n

【基本分析】

根据题意就是求解【所有子矩阵中第k大的异或和】，同时规定所有子矩阵的左上角端点为(0,0).

数据范围为10^{3,因此枚举所有右下角并每次计算子矩阵异或和的朴素做法O（m}2*n^2)不用考虑。

异或作为不进位加法，可以利用【偶数次异或结果为0】的特性实现类似【前缀和】的容斥。这使得我们可以在O(1）的复杂度内计算【某个子矩阵的异或和】

二维前缀异或&&优先队列（最小堆）

创建二维数组sum[ ] [ ],令sum[i] [j]为以(i , j)为右下角的子矩阵的异或和，

sum[i] [j] = sum[i-1] [j ] ^ sum[i] [j-1] ^ sum [i-1] [j-1] ^ matrix[i-1] [j-1];

如果所有的子矩阵异或和找到第k大的值。则变成Top K问题，可以使用【排序】或【堆】进行求解。

具体的，我们可以建立一个大小为k的小根堆，在计算二维前缀异或时，判断当前【子矩阵异或和】是否大于堆顶元素：

• 大于堆顶元素：当前子矩阵异或和可能是第k大的值，堆顶元素不可能为第K大的值。将堆顶元素弹出，并将当前子矩阵和加入堆中
• 小于堆顶元素：不会是第k大的值，直接丢弃
• 等于堆顶元素：有相同元素在堆中，直接丢弃。

最终堆顶元素即为答案

class Solution {
public:
    int kthLargestValue(vector<vector<int>>& matrix, int k) {
        //row网格行;col网格列
        int row = matrix.size();
        int col = matrix[0].size();
        //前缀和数组
        vector<vector<int>> res_matrix(row,vector<int>(col, 0));
        //最大堆查找
        priority_queue<int, vector<int>> myprique;
        int res = -1;
        res_matrix[0][0] = matrix[0][0]; 
        myprique.push(res_matrix[0][0]);
        //初始化前缀和数组，单独的行于列（为什么此处不需要判断是因为题目说明了m,n都是大于1的）
        /*
        因为m，n都大于0所以
        不需要加if(m > 0);if(n > 0)
        */
        for(int i = 1; i < row; i++)
        {
            res_matrix[i][0] = res_matrix[i-1][0] ^ matrix[i][0]; 
            myprique.push(res_matrix[i][0]);
        }
        for(int j = 1; j < col; j++)
        {
            res_matrix[0][j] = res_matrix[0][j-1] ^ matrix[0][j];
            myprique.push(res_matrix[0][j]);
        }
        //插入中间部分
        for(int i = 1; i < row; i++)
        {
            for(int j = 1; j < col; j++)
            {
                //因为没移动一次res_matrix[i-1][i-1]都重复的进行异或，所以求解前缀和的时候在于res_maitrix[i-1][i-1]异或相当于2^2-->2^2^2
                res_matrix[i][j] = res_matrix[i-1][j] ^ res_matrix[i][j-1] ^ res_matrix[i-1][j-1] ^ matrix[i][j];
                myprique.push(res_matrix[i][j]);
            }
        }
        while(k--)
        {
            res = myprique.top();
            myprique.pop();
        }
        return res;
    }
};

优化方向：用最小堆来优化，这种方法值得学习，最小堆用于维护k个元素

class Solution {
public:
    int kthLargestValue(vector<vector<int>>& matrix, int k) {
        //m：行数；n：列数
        int m = matrix.size(), n = matrix[0].size();
        //sum是前缀异或和
        //sum是怎么定义的
        int sum[m+1][n+1];
        memset(sum ,0, sizeof(sum));
        priority_queue<int, vector<int>, greater<int>> pq;
        for(int i = 1; i <= m; i++)
        {
            for(int j = 1; j <= n; j++)
            {
                
                sum[i][j] = sum[i-1][j] ^ sum[i][j-1] ^ sum[i-1][j-1] ^ matrix[i-1][j-1];
                if(pq.size() < k)
                    //最小堆保存的都是最小的
                    pq.push(sum[i][j]);
                else
                {
                    //pq里保存遍历到当前位置前k大的元素
                    if(sum[i][j] > pq.top())
                    {
                        pq.pop();
                        pq.push(sum[i][j]);
                    }
                }
            }
        }
        return pq.top();
    }
};

leetcode810:黑板异或游戏

数学归纳法，于剑指offer43，剑指offer44相同，都需要大量的数据进行推理

【题目】

黑板上写着一个非负整数数组 nums[i] 。Alice 和 Bob 轮流从黑板上擦掉一个数字，Alice 先手。如果擦除一个数字后，剩余的所有数字按位异或运算得出的结果等于 0 的话，当前玩家游戏失败。 (另外，如果只剩一个数字，按位异或运算得到它本身；如果无数字剩余，按位异或运算结果为 0。）

换种说法就是，轮到某个玩家时，如果当前黑板上所有数字按位异或运算结果等于 0，这个玩家获胜。

假设两个玩家每步都使用最优解，当且仅当 Alice 获胜时返回 true。

示例：

输入: nums = [1, 1, 2]
输出: false
解释:
Alice 有两个选择: 擦掉数字 1 或 2。
如果擦掉 1, 数组变成 [1, 2]。剩余数字按位异或得到 1 XOR 2 = 3。那么 Bob 可以擦掉任意数字，因为 Alice 会成为擦掉最后一个数字的人，她总是会输。
如果 Alice 擦掉 2，那么数组变成[1, 1]。剩余数字按位异或得到 1 XOR 1 = 0。Alice 仍然会输掉游戏。

提示：

1 <= N <= 1000
0 <= nums[i] <= 2^16

class Solution {
public:
    bool xorGame(vector<int>& nums) {
        if(nums.size() % 2 == 0)
        {
            return true;
        }
        int XOR_num = 0;
        for(int i = 0; i < nums.size(); i++)
        {
            XOR_num ^= nums[i];
        }
        return XOR_num == 0;
    }
};

图论

对于该类型题目的思路，主要有两种

1. 是连通图并且不存在环
2. 是连通图且边的个数==节点数-1

实现方式：

对于连通图的判断有两种方式

1. 以广度优先搜索或者深度优先搜索的方式，遍历一遍图。如果存在没有遍历到的节点，那么是非连通图，返回false
2. 并查集：最后如果有多个头目，则是非连通图，返回false

存在环的判定：

1. 深度优先遍历，把边给数一下。因为数的时候，会数生成树最少的边数（形成环的边会因为节点被访问过而不计算，如下图：深度遍历时，只会遍历1，2和2，3之间的边，1，3之间的边不会遍历），所以最终输出的边数<总边数，则形成环。广度优先遍历同理。
2. 并查集：如果并查集建立的过程中发生合并，则一定有环形成

/**深度优先：思路2*/
class Solution {
public:
    bool validTree(int n, vector<vector<int>>& edges) {
        /**1. 节点数==变数+1*/
        if(edges.size() +1 != n) return false;
        /**2. 连通性*/
        vector<vector<int>> Graph(n,vector<int>());
        //构造邻接表
        for(auto edge: edges){
            Graph[edge[0]].push_back(edge[1]);
            Graph[edge[1]].push_back(edge[0]);
        }
        vector<bool> visited(n);
        //深度优先
        dfs(Graph,0,visited);
        for(auto c:visited){//遍历访问数组来判定是否全部被访问过，可以优化
            if(!c) return false;
        }
        return true;  
    }
    void dfs(vector<vector<int>> &Graph, int i, vector<bool> &visited){
        if(visited[i] == true) return;
        visited[i] = true;
        for(auto c:Graph[i]){
            dfs(Graph, c, visited);
        }
    }
};

class Solution {
public:
    bool validTree(int n, vector<vector<int>>& edges) {
        /**1. 节点数==变数+1*/
        if(edges.size() +1 != n) return false;
        /**2. 连通性*/
        vector<vector<int>> Graph(n,vector<int>());
        //构造邻接表
        for(auto edge: edges){
            Graph[edge[0]].push_back(edge[1]);
            Graph[edge[1]].push_back(edge[0]);
        }
        set<int> visited;//访问过的节点放在visited数组中
        //广度优先,看是否连通
        queue<int> q;
        q.push(0);
        visited.insert(0);
        while(!q.empty()){
            int sz = q.size();
            while(sz){
                int v = q.front();
                q.pop();
                for(auto v_a : Graph[v]){
                    if(visited.find(v_a) != visited.end())//访问过了
                        continue;
                    visited.insert(v_a);
                    q.push(v_a);
                }
                sz--;
            }
        }
        return visited.size() == n;  //访问过的节点数<n,则不连通
    }
};

class Solution {
public:
    bool validTree(int n, vector<vector<int>>& edges) {
        if(n != edges.size()+1) return false;
        //并查集判断是否连通
        vector<int> parent(n);
        for(int i = 0; i < parent.size(); i++){//初始化并查集
            parent[i]=i;
        }
        for(auto edge:edges){//构造并查集
            Union(parent,edge[0],edge[1]);
        }
        int p = Find(parent,0);//得到一个头目
        for(int i = 1; i < n;i++){//如果连通，所有的头目都是p
            if(p != Find(parent, i))
                return false;
        }
        return true;
    }
    void Union(vector<int> &parent, int A, int B){
        int pa = Find(parent, A);
        int pb = Find(parent, B);
        if(pa != pb){//祖先不同，把其中一个人的祖先，换成另一个
            parent[pa] = pb;
        }
    }
    int Find(vector<int> &parent, int A){
        while(parent[A] != A){
            A = parent[A];
        }
        return A;
    }
};

并查集

并查集可以解决什么问题：

主要就是集合问题，两个节点在不在一个集合，也可以将两个节点添加到一个集合中。

并查集模板如下：

	int n = 1005;//节点数量3到1000
	int pre[1005];
	//并查集初始化
	void init()
	{
		for (int i = 0; i < n; i++)
		{
			pre[i] = i;
		}
	}
//并查集寻根过程
	int Find(int x)
	{
		if (x == pre[x])
			return pre[x];
		else
		{
			return Find(pre[x]);
		}
	}
	//将v->u这条边加入并查集
	void Union(int u, int v)
	{
		int t1 = Find(u);
		int t2 = Find(v);
		if (t1 != t2)
			pre[t2] = t1;
	}
//判断u和v是否到同一个根
bool same(int u, int v)
{
    u = find(u);
    v = find(v);
    return u == v;
}

模板总结，只要修改n和pre数组的大小就可以了

并查集主要功能：

• 寻找根节点，Find(int x),也就是判断这个节点的祖先节点是那个
• 将两个节点接到同一个集合，Uoin(int u, int v)将两个节点连在同一个根节点上
• 判断两个节点是否在同一个集合，same(int u, int v)，就是判断两个 节点是不是同一个根节点

【思路】

无向图，返回一条可以删去的边，使得结果图是一个有着N个节点的树。

如果有多个答案，则返回二维数组中最后出现的边。那么我们就可以从前向后遍历每一条边，边的两个节点如果不在同一个集合，就加入集合（即：同一个根节点）。

如果边的两个节点已经出现在同一个集合里，说明这边的两个节点已经连在一起，如果再加入这条边一定就出现环了。

class Solution {
    int n = 1005;
    int pre[1005];
    //并查集初始化
    void init()
    {
        for(int i = 0; i < n; i++)
        {
            pre[i] = i;
        }
    }
    //并查集寻根过程
    int Find(int x)
    {
        if(x == pre[x])
            return pre[x];
        else
            return Find(pre[x]);
    }
    //将v->u这条边加入并查集
    void Union(int u, int v)
    {
        int t1 = Find(u);
        int t2 = Find(v);
        if(t1 != t2)
        {
            pre[t2] = t1;
        }
    }
    //判断u和v是否同根
    bool same(int u, int v)
    {
        u = Find(u);
        v = Find(v);
        return u == v;
    }
public:
    vector<int> findRedundantConnection(vector<vector<int>>& edges) {
        init();
        for(int i = 0; i < edges.size(); i++)
        {
            if(same(edges[i][0], edges[i][1]))
                return edges[i];
            else
                Union(edges[i][0], edges[i][1]);
        }
        return {};
    }
};

leetcode：朋友圈（可以尝试着使用广度优先遍历）

【题目】

班上有N名同学，其中有些人时朋友，有些则不是。他们的友谊具有传递性。如果已知A是B的朋友，B是C的朋友，那么我们可以认为A也是C的朋友。所谓的朋友圈，是指所有朋友的集合。

给定一个N*M的矩阵M，表示班级中学生之间的朋友关系。如果M[i] [j] = 1,表示已知第i个和第j个学生互为朋友关系，否则为不知道，你必须输出所有学生中的已知的朋友圈总数。

输入：
[[1,1,0],
[1,1,0],
[0,0,1]]
输出：
2
解释：已知学生0和学生1互为朋友，他们在一个朋友圈。第2个学生子集在一个朋友圈，所以返回2

输入：
[[1,1,0],
[1,1,1],
[0,1,1]]
输出：
1
解释：已知学生0和学生1互为朋友，学生1和学生2互为朋友，所以学生0和学生2也是朋友，所以他们三个在一个朋友圈返回1

提示：

1. 1 <= N <= 200
2. M[i] [i] == 1
3. M[i] [j] == M[j] [i]

[c++]

class Solution1{
	int pre[10000];
	void init()
	{
		for (int i = 0; i < 1000; i++)
		{
			pre[i] = i;
		}
	}
	int Find(int x)
	{
		if (x == pre[x])
			return pre[x];
		else
		{
			return Find(pre[x]);
		}
	}
	void Union(int u, int v)
	{
		int t1 = Find(u);
		int t2 = Find(v);
		if (t1 != t2)
			pre[t2] = t1;
	}
public:
	int findCircleNum(vector<vector<int>>& M)
	{
		init();
		for (int i = 0; i < M.size(); i++)
		{
			for (int j = 0; j < M[0].size(); j++)
			{
				if(M[i][j] == 1)
					Union(i, j);
			}
		}
		int count = 0;
		for (int i = 0; i < M.size(); i++)
		{
			if (pre[i] == i)
				count++;
		}
		return count;
	}
};

int main()
{
	vector<vector<int>> M = { { 1, 1, 0 }, { 1, 1, 0 }, { 0, 0, 1 } };
	cout << "朋友圈的数量为：" << Solution1().findCircleNum(M) << endl;
	system("pause");
	return 0;
}

leetcode323：无向图中联通分量的数目（并查集）

给定编号从 0 到 n-1 的 n 个节点和一个无向边列表（每条边都是一对节点），请编写一个函数来计算无向图中连通分量的数目。

示例 1:

输入: n = 5 和 edges = [[0, 1], [1, 2], [3, 4]]

 0          3
 |          |
 1 --- 2    4 

输出: 2
示例 2:

输入: n = 5 和 edges = [[0, 1], [1, 2], [2, 3], [3, 4]]

 0           4
 |           |
 1 --- 2 --- 3

输出: 1
注意:
你可以假设在 edges 中不会出现重复的边。而且由于所以的边都是无向边，[0, 1] 与 [1, 0] 相同，所以它们不会同时在 edges 中出现。

【解题】

并查集与朋友圈问题相同

广度优先遍历BFS与深度优先遍历DFS都需要建立连接表

//并查集
class Solution {
    int pre[10000];
	void init()
	{
		for (int i = 0; i < 1000; i++)
		{
			pre[i] = i;
		}
	}
	int Find(int x)
	{
		if (x == pre[x])
			return pre[x];
		else
		{
			return Find(pre[x]);
		}
	}
	void Union(int u, int v)
	{
		int t1 = Find(u);
		int t2 = Find(v);
		if (t1 != t2)
			pre[t2] = t1;
	}
public:
    int countComponents(int n, vector<vector<int>>& edges) {
        init();
        for(int i = 0; i < edges.size(); i++)
        {
            Union(edges[i][0],edges[i][1]);
        }
        int count = 0;//统计个数
        
        for(int i = 0; i < n; i++)
        {
            if(pre[i] == i)
                count++;
        }
        return count;
    }
};