[数据结构与算法]记一次三维动态规划（股票买卖最佳时机）的优化，耗时从击败(20%5%)到击败(99%65%)

力扣的股票买卖问题如下。123题k=2，188题k不定。

给定一个整数数组 prices ，它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。

采用动态规划。
状态转移图：

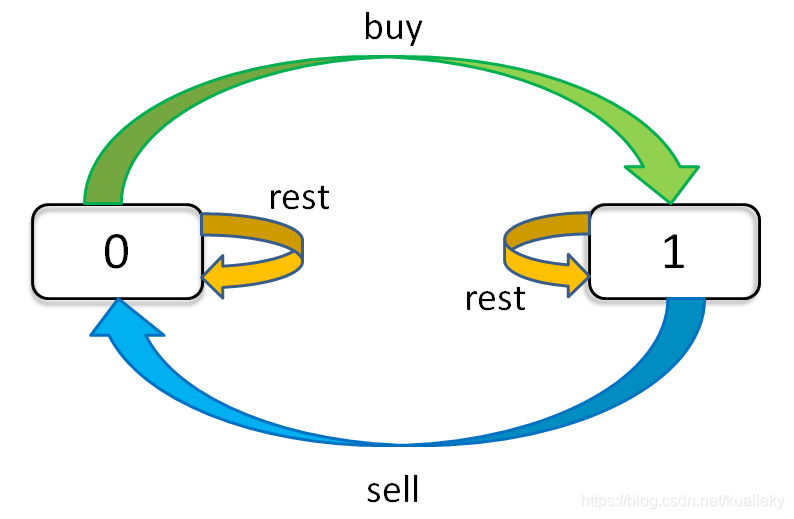
这个问题的「状态」有三个，第一个是天数，第二个是允许交易的最大次数，第三个是当前的持有状态。所以这是个三维DP问题。
状态转移方程：
dp[i][k][j]：i 为天数，k为最多交易天数，j为当前是否持有。

dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])

123. 买卖股票的最佳时机 III
①动态规划 （通用模板）

class Solution {
    public int maxProfit(int[] prices) {
        int n = prices.length;
        int max_k = 2;
        int[][][] dp = new int[n][max_k + 1][2];
        dp[0][1][1] = - prices[0];
        dp[0][2][1] = - prices[0];
        for (int i = 1; i < n; i++) {
            for (int k = 1; k <= max_k; ++k) {
                dp[i][k][0] = Math.max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
                dp[i][k][1] = Math.max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]);
            }
        }
        return dp[n-1][max_k][0];
    }
}

②由以上代码可知，i 依赖 i - 1， 先把i给压缩了（通用模板）（优化）

class Solution {
    public int maxProfit(int[] prices) {
        int n = prices.length;
        int max_k = 2;
        int[][] dp = new int[max_k + 1][2];
        dp[1][1] = - prices[0];
        dp[2][1] = - prices[0];
        for (int i = 1; i < n; i++) {
            for (int k = max_k; k >= 1; --k) { //这里就得从大到小了，因为dp[k][1]依赖上一阶段的dp[k-1][0]，先计算k-1就不为上一阶段了
                dp[k][0] = Math.max(dp[k][0], dp[k][1] + prices[i]);
                dp[k][1] = Math.max(dp[k][1], dp[k-1][0] - prices[i]);
            }
        }
        return dp[max_k][0];
    }
}

③由以上代码可知，k只取1或2， 再把k给展开

class Solution {
    public int maxProfit(int[] prices) {
        int n = prices.length;
        int max_k = 2;
        int[][] dp = new int[max_k + 1][2];
        dp[1][1] = - prices[0];
        dp[2][1] = - prices[0];
        for (int i = 1; i < n; i++) {
            dp[2][0] = Math.max(dp[2][0], dp[2][1] + prices[i]);
            dp[2][1] = Math.max(dp[2][1], dp[1][0] - prices[i]);
            dp[1][0] = Math.max(dp[1][0], dp[1][1] + prices[i]);
            dp[1][1] = Math.max(dp[1][1], dp[0][0] - prices[i]);
        }
        return dp[max_k][0];
    }
}

④最后一维j，只取1（持有）或0（未持有）， k和j一共4(2*2)种情况，一起展开。

class Solution {
    public int maxProfit(int[] prices) {
        int n = prices.length;
        int i_1_0 = 0;
        int i_2_0 = 0;
        int i_1_1 = -prices[0];
        int i_2_1 = -prices[0];
        for (int i = 1; i < n; i++) {
            i_2_0 = Math.max(i_2_0, i_2_1 + prices[i]);
            i_2_1 = Math.max(i_2_1, i_1_0 - prices[i]);
            i_1_0 = Math.max(i_1_0, i_1_1 + prices[i]);
            i_1_1 = Math.max(i_1_1, - prices[i]);
        }
        return i_2_0;
    }
}

188. 买卖股票的最佳时机 IV
k由定值2变为了不定值。上题搞懂了，这题不是秒？

class Solution {
    public int maxProfit(int k, int[] prices) {
        int n = prices.length;
        if(n <= 1) return 0;
        int[][] dp = new int[k + 1][2];
        for (int i = 0; i < n; i++) {
            for (int j = k; j >= 1; --j) {
                if (i == 0) {
                    dp[j][1] = - prices[0];
                }
                dp[j][0] = Math.max(dp[j][0], dp[j][1] + prices[i]);
                dp[j][1] = Math.max(dp[j][1], dp[j-1][0] - prices[i]);
            }
        }
        return dp[k][0];
    }
}