[数据结构与算法] 剑指Offer中遇到的问题

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 剑指Offer中遇到的问题 -> 正文阅读

[数据结构与算法]剑指Offer中遇到的问题

总结

第26、27、28、32-3、33、34、36题，不会做。好好看看

39 40 42 45都不是很难，而且有一定的技巧。46题一时没有想起来好的解决办法。49也需要一定的技巧

59-1好好做做

03 数组中重复的数字

class Solution {
    //遍历数组，使得下标i位置上的值num[i]==i
    public static int findRepeatNumber(int[] nums) {
        for(int i = 0; i < nums.length; i++){
            while(nums[i] != i){
                //题目已经说了：长度为 n 的数组 nums 里的所有数字都在 0～n-1 的范围内。
                //所以nums[i]的值不会超过数组的长度。
                if(nums[i] == nums[nums[i]]){
                    return nums[i];
                }else{
                    swap(nums, i, nums[i]);
                }
            }
        }
        return -1;
    }

    public static void swap(int[] arr, int a, int b){
        int temp = arr[a];
        arr[a] = arr[b];
        arr[b] = temp;
    }
}

09 用两个栈实现队列

Stack过于古老，并且实现地非常不好，因此现在基本已经不用了，可以直接用Deque来代替Stack进行栈操作。

因为Stack继承了Vector接口，而Vector底层是AbstractList，是一个数组，那么就要考虑空间扩容的问题了。可以使用LinkedList来做Stack的容器，因为LinkedList实现了Deque接口，所以Stack能做的事LinkedList都能做，其本身结构是个链表，扩容消耗少。但是我的意思不是像100%代码那样直接使用一个List当做队列，那确实是快，但是不符题意。贴上代码，这样的优化之后，效率提高了40%，超过97%。

应该使用Stack<Integer> stack = new LinkedList<>();代替Stack<Integer> stack = new Stack<>();

10-1 斐波那契数列

使用动态规划

    public static int numWays(int n) {

    	int a = 1, b = 1;
    	int sum = 0;
    	for(int i = 0; i < n; i++){
    		sum = (a + b) % 1000000007;
    		a = b;
    		b = sum;
    	}
    	return a;
    }

13 机器人的运动范围

自己没有写出来

使用DFS或BFS

14-2 剪绳子

贪心算法：自己实现一下很简单

大数求余：xy%p = [(x % p) * (y % p)] % p

使用二分法求余数。

易错点：因为数比较大，很容易超过int64，所以要用long类型，但是最后返回的是int类型。

正确写法：return (int)(mod(a) * b % 1000000007);

一定要加括号，return (int)mod(a) * b % 1000000007;不加括号的话，就会先转换为int在求余，此时已经超过范围了。

15 二进制中1的个数

题目给的是输入无符号数，但是java中没有无符号数，输入int型的数据，如果首位为1，就会把它当成负数算。

//普通方法不可行，当第32位为1时，就会把这个数当成负数。
public static int hammingWeight(int n) {
    int count = 0;
    while(n != 0){
        if(n % 2 == 1){
            count++;
        }
        n /= 2;
    }
    return count;
}

该题目常规解法应该使用位运算，无符号右移>>>，有符号右移>>

而且还有一个奇淫技巧： n &= n - 1 ： 消去数字 n 最右边的 1 。

16 数值的整数次方

快速幂

n的二进制表示如下：

$n = 1 * b_1 + 2 * b_2 + 4 * b_3 + 8 * b_4 + ..., b=0或1$

$a^n = a^{1 * b_1 + 2 * b_2 + 4 * b_3 + 8 * b_4 + ...} = a^{1*b_1} * a^{2*b_2} * a^{4*b_3} * a^{8*b_4} * ...$

将 $a^n$ 分解成如上的形式，可将时间复杂度有O(N)降为O(lgN)

注意：n的范围为[?2147483648,2147483647]，防止n为?2147483648时，-n越界，故使用一个long类型的变量代替整型的n，如long longN = n;

要会使用位运算，使用(n&1)来判断最后一位是否为1。

19 正则表达式匹配

太难了，先不做。

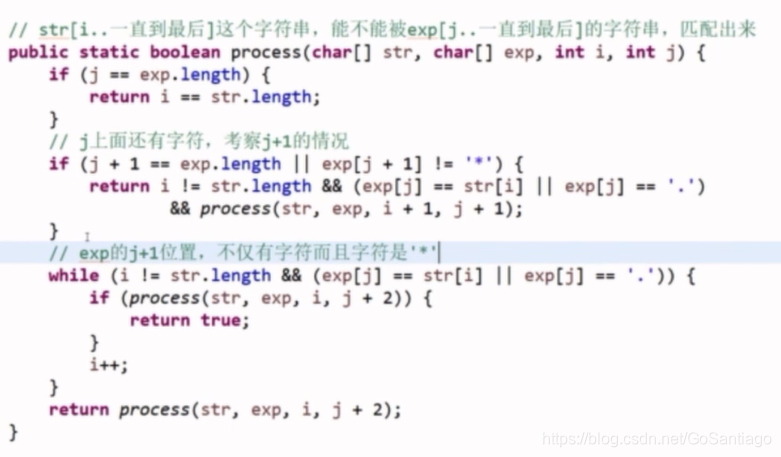
在这里插入图片描述

动态规划，在进阶班第八节最后一题讲的

20 表示数值的字符串

扣边界的题目，思路不对，就很麻烦。

正确解法

public static boolean isNumber(String s) {
    if(s == null || s.length() == 0){
        return false;
    }
    //标记是否遇到相应情况
    boolean numSeen = false;
    boolean dotSeen = false;
    boolean eSeen = false;
    char[] str = s.trim().toCharArray();
    for(int i = 0;i < str.length; i++){
        if(str[i] >= '0' && str[i] <= '9'){
            numSeen = true;
        }else if(str[i] == '.'){
            //.之前不能出现.或者e
            if(dotSeen || eSeen){
                return false;
            }
            dotSeen = true;
        }else if(str[i] == 'e' || str[i] == 'E'){
            //e之前不能出现e，必须出现数
            if(eSeen || !numSeen){
                return false;
            }
            eSeen = true;
            numSeen = false;//重置numSeen，排除123e或者123e+的情况,确保e之后也出现数
        }else if(str[i] == '-' || str[i] == '+'){
            //+-出现在0位置或者e/E的后面第一个位置才是合法的
            if(i != 0 && str[i-1] != 'e' && str[i-1] != 'E'){
                return false;
            }
        }else{//其他不合法字符
            return false;
        }
    }
    return numSeen;
}

错误解法

//错误解法，没有过测试用例
public static boolean isNumber(String s) {
    if(s == null || s.length() == 0) return false;
    s = s.trim();
    if(s.length() == 0) return false;
    char[] arr = s.toCharArray();
    for(int i = 0; i < arr.length; i++){
        if(arr[i] == '.'){
            //小数点前可以没有数字数字
            //if(i == 0) return false;
            if(i > 0 && i == arr.length - 1) return true;//小数点能放最后一个,只不过前面必须有数字
            if(arr.length == 1) return false;//防止字符串中只有一个小数点
            int j = i + 1;
            while(j < arr.length){//小数点后必须全为数字
                if(arr[j] < '0' || arr[j] > '9'){
                    return false;
                }
                j++;
            }
            return true;
        }else if(arr[i] == 'e' || arr[i] == 'E'){
            if(i == 0) return false;
            if(i == arr.length - 1) return false;//e不能放最后一个
            int j = i + 1;
            if(arr[i + 1] == '+' || arr[i + 1] == '-'){
                j = i + 2;
            }
            if(j == arr.length) return false;
            while(j < arr.length){//e之后除了能接正负号外，其余的全为数字
                if(arr[j] < '0' || arr[j] > '9'){
                    return false;
                }
                j++;
            }
            return true;
        }else if(arr[i] == '+' || arr[i] == '-'){
            if(i > 0 && (arr[i - 1] != 'e' && arr[i - 1] != 'E')){//正负号前面有数字或者e
                return false;
            }else if(i < arr.length - 1){//正负号后面必须有数字或者e
                if((arr[i + 1] <= '9' && arr[i + 1] >= '0') || arr[i + 1] == 'e' || arr[i] == 'E'){
                }else{
                    return false;
                }
            }else if(i == arr.length - 1){
                return false;
            }
        }else if(arr[i] >= '0' && arr[i] <= '9'){
            ;
        }else{
            return false;
        }
    }
    return true;
}

26 树的子结构

虽然做出来了，但是代码不够简洁

27 二叉树的镜像

自己写的代码总是太过复杂

28 对称的二叉树

我本使用的是求二叉树的中序遍历，如果遍历结果对称，则二叉树对称，这个想法是错误的。如[1,2,2,2,null,2]

另一种办法也不可行：先对二叉树进行镜像操作。然后比较操作前后中序遍历。上面的例子同样可以验证该方法不可行。

32-2 从上到下打印二叉树

每次只遍历一层的节点，可以用size()来判断

32-3 从上到下打印二叉树

不要使用反转链表试试

33 *二叉搜索树的后续遍历序列

递归：自己尝试的时候还需要创建数组，直接使用下标就行。

public static boolean verifyPostorder(int[] postorder) {
    return process(postorder, 0, postorder.length - 1);
}
public static boolean process(int[] arr, int a, int b){
    if(a >= b) return true;
    int root = arr[b];
    int i = a;
    for(i = a; i < b; i++){
        if(arr[i] > root){
            break;
        }
    }
    while(i < b){
        if(arr[i] < root){
            return false;
        }
        i++;
    }
    return process(arr, a, i - 1) && process(arr, i, b - 1);
}

第二种方法：单调栈

34 **二叉树中和为某一值的路径

递归转换为回溯

class Solution {
    // public static List<List<Integer>> pathSum(TreeNode root, int sum){
    //     List<List<Integer>> lists = new LinkedList<>();
    //     LinkedList<Integer> list = new LinkedList<>();
    //     process(lists, list, root, sum);
    //     return lists;
    // }

    // public static void process(List<List<Integer>> lists, LinkedList<Integer> list, TreeNode root, int sum){
    //     if(root == null){
    //         return;
    //     }
    //     list.add(root.val);
    //     sum -= root.val;
    //     if(root.left == null && root.right == null && sum == 0){
    //         lists.add(new LinkedList<>(list));
    //     }
    //     process(lists, list, root.left, sum);
    //     process(lists, list, root.right, sum);
    //     list.removeLast();
    // }
    static List<List<Integer>> lists = new LinkedList<>();

    public static List<List<Integer>> pathSum(TreeNode root, int sum) {
        lists.clear();
        if(root == null) return lists;
        List<Integer> list = new LinkedList<>();
        path(root, sum, list);
        return lists;
    }

    private static void path(TreeNode root, int sum, List<Integer> list) {
        sum -= root.val;
        if(root.left == null && root.right == null){
            if(0 == sum) {
                List<Integer> result = new LinkedList<>(list);
                result.add(root.val);
                lists.add(result);
            }
            return;
        }
        if(root.left != null){
            list.add(root.val);
            path(root.left, sum, list);
            list.remove(list.size() - 1);
        }
        if(root.right != null){
            list.add(root.val);
            path(root.right, sum, list);
            list.remove(list.size() - 1);
        }
    }
}

36 **二叉搜索树与双向链表

中序遍历递归形式

class Solution {
    public Node pre;
    public Node head, tail;
    public void process(Node root){
        if(root == null){
            return;
        }
        process(root.left);
        root.left = pre;
        if(pre == null){
            head = root;
        }else{
            pre.right = root;
        }
        pre = root;
        tail = root;
        process(root.right);
    }
    public Node treeToDoublyList(Node root) {
        if(root == null){
            return null;
        }
        process(root);
        tail.right = head;
        head.left = tail;
        return head;
    }
}

中序遍历非递归

public static Node treeToDoublyList(Node root) {
    if(root == null) return null;
    LinkedList<Node> stack = new LinkedList<>();
    Node head = null;
    Node pre = null, tail = null;
    Node cur = root;
    while(cur != null || !stack.isEmpty()){
        if(cur != null){
            stack.push(cur);
            cur = cur.left;
        }else{
            Node out = stack.pop();
            if(pre == null){
                pre = out;
                head = pre;
            }else{
                out.left = pre;
                pre.right = out;
                pre = out;
            }
            cur = out.right;
            tail = pre;
        }
        if(head != null) head.left = tail;
        if(tail != null) tail.right = head;
    }
    return head;
}

37 序列化二叉树

在这里插入图片描述

以下是我自己写的

package four;

import java.util.LinkedList;
import java.util.Queue;

public class Solution_37 {
    public static class TreeNode{
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode(int val){
            this.val = val;
        }
    }
    // Encodes a tree to a single string.
    public static String serialize(TreeNode root) {
        if(root == null){
            return "";
        }
        Queue<TreeNode> nodeQueue = new LinkedList<>();
        StringBuilder res = new StringBuilder();
        nodeQueue.add(root);
        while(!nodeQueue.isEmpty()){
            TreeNode node = nodeQueue.poll();
            if(node == null){
                res.append("null,");
            }else{
                res.append(node.val).append(",");
                if(node.left == null && node.right == null && nodeQueue.isEmpty()){
                    continue;
                }
                nodeQueue.add(node.left);
                nodeQueue.add(node.right);
            }
        }
        res.deleteCharAt(res.length() - 1);
        return res.toString();
    }

    // Decodes your encoded data to tree.
    public static TreeNode deserialize(String data) {
        if(data.equals("")){
            return null;
        }
        String[] nodes = data.split(",");
        Queue<TreeNode> nodeQueue = new LinkedList<>();
        for (String node : nodes) {
            if (!node.equals("null")) {
                nodeQueue.add(new TreeNode(Integer.parseInt(node)));
            } else {
                nodeQueue.add(null);
            }
        }
        TreeNode root = nodeQueue.peek();
        //复制一份链表，并没有新建链表中的节点，两个链表包含的节点是相同的
        Queue<TreeNode> children = new LinkedList<>(nodeQueue);
        children.poll();
        while(!children.isEmpty()){
            TreeNode node = nodeQueue.poll();
            if(node != null){
                node.left = children.poll();
                node.right = children.poll();
            }
        }
        return root;
    }

    public static void main(String[] args) {
        TreeNode node1 = new TreeNode(1);
        TreeNode node2 = new TreeNode(2);
        TreeNode node3 = new TreeNode(3);
        node1.left = node2;
        node2.right = node3;
        String res = serialize(node1);
        System.out.println(res);
        System.out.println("---------");
        TreeNode root = deserialize(res);
        String res2 = serialize(root);
        System.out.println(res2);
    }
}

反序列化我写的不好，下面是人家的

    //从队列中弹出节点，在字符数组中找其的左右孩子，如果其某个孩子不为null，新建一个节点入队
    public static TreeNode deserialize2(String data){
        if(data.equals("")){
            return null;
        }
        String[] nodes = data.split(",");
        Queue<TreeNode> nodeQueue = new LinkedList<>();
        TreeNode root = new TreeNode(Integer.parseInt(nodes[0]));
        nodeQueue.add(root);
        int i = 1;
        while(!nodeQueue.isEmpty()){
            TreeNode node = nodeQueue.poll();
            //该节点的左孩子
            if(nodes[i].equals("null")){
                node.left = null;
            }else{
                node.left = new TreeNode(Integer.parseInt(nodes[i]));
                nodeQueue.add(node.left);
            }
            i++;
            //该节点的右孩子
            if(nodes[i].equals("null")){
                node.right = null;
            }else{
                node.right = new TreeNode(Integer.parseInt(nodes[i]));
                nodeQueue.add(node.right);
            }
            i++;
        }
        return root;
    }

38 字符串的排列

使用如下代码超出时间限制

package four;

import java.util.ArrayList;
import java.util.Arrays;

class Solution_38 {

    //每次增加固定前缀的个数，对后面的进行全排列
    public static String[] permutation(String str) {
        ArrayList<String> lists = new ArrayList<String>();
        char[] arr = str.toCharArray();
        Arrays.sort(arr);//使用工具类java.util.Arrays进行排序
        process(lists, arr, 0, arr.length - 1);
        int len = lists.size();
        String[] strings = new String[len];
        for(int i = 0; i < len; i++){
            strings[i] = lists.get(i);
        }
        return strings;
    }

    public static void process(ArrayList<String> lists, char[] arr, int begin, int end){
        if(begin == end){
            String temp = String.valueOf(arr);
            if(!lists.contains(temp)){
                lists.add(temp);
            }
            return;
        }else{
            process(lists, arr, begin + 1, end);
            for(int i = begin + 1; i <= end; i++){
                swap(arr, begin, i);
                process(lists, arr, begin + 1, end);
                swap(arr, begin, i);
            }
        }
    }

    public static void swap(char[] arr, int m, int n){
        char temp = arr[m];
        arr[m] = arr[n];
        arr[n] = temp;
    }

    public static void main(String[] args){
        String str = "abc";
        String[] lists = permutation(str);
        for(String s: lists){
            System.out.println(s);
        }
    }
}

原因是使用ArrayList的时候，需要判断是否添加过该链表

if(!lists.contains(temp)){
    lists.add(temp);
}

使用HashSet解决此问题。

另外，arr[i] == arr[begin]可减少重复的循环

for(int i = begin + 1; i <= end; i++){
    if(arr[i] == arr[begin]){
        continue;
    }
    swap(arr, begin, i);
    process(lists, arr, begin + 1, end);
    swap(arr, begin, i);
}

最后通过的代码为

package four;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.HashSet;
import java.util.Set;

class Solution_38 {

    //每次增加固定前缀的个数，对后面的进行全排列
    public static String[] permutation(String str) {
        //使用ArrayList，往里面添加链表的时候，需要判断是否添加过，耗时
        Set<String> lists = new HashSet<String>();
        char[] arr = str.toCharArray();
        Arrays.sort(arr);//使用工具类java.util.Arrays进行排序
        process(lists, arr, 0, arr.length - 1);
        int len = lists.size();
        return lists.toArray(new String[len]);
    }

    public static void process(Set<String> lists, char[] arr, int begin, int end){
        if(begin == end){
            String temp = String.valueOf(arr);
                lists.add(temp);
            return;
        }else{
            process(lists, arr, begin + 1, end);
            for(int i = begin + 1; i <= end; i++){
                if(arr[i] == arr[begin]){
                    continue;
                }
                swap(arr, begin, i);
                process(lists, arr, begin + 1, end);
                swap(arr, begin, i);
            }
        }
    }

    public static void swap(char[] arr, int m, int n){
        char temp = arr[m];
        arr[m] = arr[n];
        arr[n] = temp;
    }

    public static void main(String[] args){
        String str = "kzfxxx";
        String[] lists = permutation(str);
        for(String s: lists){
            System.out.println(s);
        }
    }
}

39 数组中出现次数超过一半的数字

使用摩尔投票法更简单

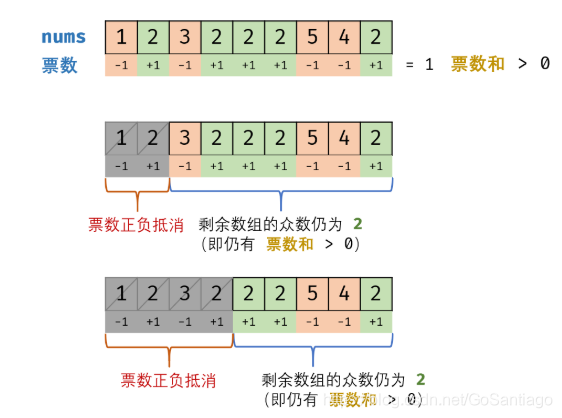
在这里插入图片描述

40 ***最小的K个数

面试最常问，可以使用堆、快排、BFPRT

使用改进的快排

public static int[] getLeastNumbers(int[] arr, int k) {
    quickSort(arr, 0, arr.length - 1, k);
    return Arrays.copyOf(arr, k);
}

public static void quickSort(int[] arr, int l, int r, int k){
    if(l < r){
        int[] temp = partition(arr, l, r);
        if(temp[0] > k){
            quickSort(arr, l, temp[0] - 1, k);
        }else if(temp[1] < k){
            quickSort(arr, temp[0] + 1, r, k);
        }
    }
}

public static int[] partition(int[] arr, int l, int r){
    int num = arr[r];
    int left = l - 1;
    int right = r;
    int cur = l;
    while(cur < right){
        if(arr[cur] < num){
            swap(arr, ++left, cur++);
        }else if(arr[cur] == num){
            cur++;
        }else{
            swap(arr, --right, cur);
        }
    }
    swap(arr, right, r);
    return new int[]{left + 1, right};
}

public static void swap(int[] arr, int a, int b){
    int temp = arr[a];
    arr[a] = arr[b];
    arr[b] = temp;
}

42 连续子数组的最大和

把问题想得复杂了。其实很简单，8行代码就能搞定

43 1-n整数中1出现的次数

解题思路
f(n))函数的意思是1～n这n个整数的十进制表示中1出现的次数，将n拆分为两部分，最高一位的数字high和其他位的数字last，分别判断情况后将结果相加，看例子更加简单。

例子如n=1234，high=1, pow=1000, last=234

可以将数字范围分成两部分1-999和1000-1234

1~999这个范围1的个数是f(pow-1)
1000~1234这个范围1的个数需要分为两部分：
千分位是1的个数：千分位为1的个数刚好就是234+1(last+1)，注意，这儿只看千分位，不看其他位
其他位是1的个数：即是234中出现1的个数，为f(last)
所以全部加起来是f(pow-1) + last + 1 + f(last);

例子如3234，high=3, pow=1000, last=234

可以将数字范围分成两部分1-999，1000-1999，2000-2999和3000-3234

1 ~ 999这个范围1的个数是f(pow-1)
1000~1999这个范围1的个数需要分为两部分：
千分位是1的个数：千分位为1的个数刚好就是pow，注意，这儿只看千分位，不看其他位
其他位是1的个数：即是999中出现1的个数，为f(pow-1)
2000~2999这个范围1的个数是f(pow-1)
3000~3234这个范围1的个数是f(last)
所以全部加起来是pow + high*f(pow-1) + f(last);

class Solution {
    public int countDigitOne(int n) {
        return f(n);
    }
    private int f(int n ) {
        if (n <= 0)
            return 0;
        String s = String.valueOf(n);
        int high = s.charAt(0) - '0';
        int pow = (int) Math.pow(10, s.length()-1);
        int last = n - high*pow;
        if (high == 1) {
            return f(pow-1) + last + 1 + f(last);
        } else {
            return pow + high*f(pow-1) + f(last);
        }
    }
}

45 把数组排成最小的数

如果会用字符串比较string1.compraeTo(string2)，就会简单很多。

46 把数字翻译成字符串

暴力递归转动态规划

47 礼物的最大值

这是一道比较简单的动态规划。

空间复杂度可以为O(1)，不要重新建立二维数据。

48 最长不含重复字符的字符串

很明显用滑动窗口，使用一个HashMap判断窗口中是否含有要加入的字符，如果有，则按照加入HashMap的顺序删除map中的元素，直到map中不含该元素。

如何按照加入顺序删除，刚开始我是用了两个HashMap，键值分别为HashMap<Character,Integer> map1和HashMap<Integer, Character> map2，加入的时候，key对应的value从0增加。如果窗口中存在字符C，就从map2中根据最小的索引获取字符，然后到map1中删除该字符，直到map1中没有要加入的那个字符。

最长不含重复字符的字符串就是窗口的长度

上面的操作可以简化，其实不需要使用两个hashMap，忽略了一点，可以根据进入窗口的顺序来获取进入HashMap的顺序。窗口中最左边的肯定是最早进入map的。所以

while(map.containsKey(c)){
    map.remove(string.charAt(left++));
}

如上就可以按加入map的顺序删除元素，同时窗口缩小。

原来的复杂代码，如下，大大浪费了空间。

if(map.containsKey(c)){
    while(map.containsKey(c)){
        char temC = map2.get(delIndex);
        map2.remove(delIndex);
        map.remove(temC);
        delIndex++;
        left++;
    }
    right++;
    map.put(c, index);
    map2.put(index, c);
    index++;
}

49 丑数

丑数的递推性质： 由于丑数只包含因子 2, 3, 5 ，因此较大的丑数一定能够通过 某较小丑数 × 某因子 得到。

我也知道以上原理，但是不知道怎么动态规划。

我的做法是，是使用一个Set，每遇到一个丑数，将其放入Set中。

如何判断遇到的是丑数呢？

每遇到一个数，先判断其能否2整除，能被2整除，且商在Set中，则该数也是丑数
如果不能被2整除，能被3整除，且商在Set中，则该数也是丑数
如果不能被3整除，能被5整除，且商在Set中，则该数也是丑数
如果不能被2或3或5整除，则不是丑数

但是这个方法超出时间限制。应该使用动态规划。

动态规划的思想：

一个数能被2整除，假如这个数是18，除以2商为9，9为丑数，则18也是丑数。下一个能被2整除的丑数的商肯定比9大，比如丑数20，除以2的商为10。
一个数能被3整除，假如这个数是15，除以3商为5，5为丑数，则15也是丑数。下一个能被3整除的丑数的商肯定比5大，比如丑数27，除以3的商为9。
一个数能被5整除，假如这个数是5，除以5商为1，1为丑数，则5也是丑数。下一个能被5整除的丑数的商肯定比1大，比如丑数25，除以5的商为5。

所以可以添加三个索引，分别标记上一步分别被2、3、5整除后的商

class Solution {
    public int nthUglyNumber(int n) {
        int a = 0, b = 0, c = 0;
        int[] dp = new int[n];
        dp[0] = 1;
        for(int i = 1; i < n; i++) {
            int n2 = dp[a] * 2, n3 = dp[b] * 3, n5 = dp[c] * 5;
            dp[i] = Math.min(Math.min(n2, n3), n5);
            if(dp[i] == n2) a++;
            if(dp[i] == n3) b++;
            if(dp[i] == n5) c++;
        }
        return dp[n - 1];
    }
}

51 ***数组中的逆序对

一个数组arr，长度为len，那么能构成 $count = {len*(len-1)/2}$ 个数对，数对的下标分别是(0,1)、(0,2)、(0,3)、...、(0,len - 1)、(1,2)、(1,3)、...、(1,len - 1)、...、(len - 3,len - 2)、(len - 3,len - 1)、(len - 2,len - 1)。但是这些数组对中有些不构成逆序，而且还有的数对中元素相等。我们尝试把这写逆序找出来。

怎么做，对原数组进行插入排序，在排序的过程中，每进行一次交换，交换次数sum加一。遇到相等元素，也要交换，（主要是为了让sum加一，不执行交换操作也行），这样就使得数组中的元素相等的情况也统计出来了。

最后总的逆序对数为 ${count - sum}$

如下面的代码，代码是正确的，就是超时了，使用归并排序能降低一点复杂度

public static int reversePairs(int[] nums) {
    int len = nums.length;
    int sum = 0;
    for(int i = 1; i < len; i++){
        int j = i - 1;
        int k = i;
        while(j >= 0){
            if(nums[j] <= nums[k]){
                swap(nums, j--, k--);
                sum++;
            }else{
                break;
            }
        }
    }
    int count;
    //主要是为了防止两个数相乘，超过int32的范围
    if((len & 1) == 1){
        count = len * ((len - 1) >> 1);
    }else {
        count = (len >> 1) * (len - 1);
    }
    return count - sum;
}
public static void swap(int[] nums, int a, int b){
    int temp = nums[a];
    nums[a] = nums[b];
    nums[b] = temp;
}

归并排序

static int count = 0;
public static int reversePairs2(int[] nums) {
    if(nums == null || nums.length < 2){
        return 0;
    }
    mergeSort(nums, 0, nums.length - 1);
    return count;
}

public static void mergeSort(int[] nums, int a, int b){
    if(b == a) return;
    int mid = ((b - a) >> 1) + a;
    mergeSort(nums, a, mid);
    mergeSort(nums, mid + 1, b);
    merge(nums, a, mid, b);
}

public static void merge(int[] nums, int a, int mid, int b){
    int[] help = new int[b - a + 1];
    int index = 0;
    int L = a, R = mid + 1;
    while(L <= mid && R <= b){
        //注意此处是大于号，要理清逻辑关系
        if(nums[L] > nums[R]){
            //如果左边数组中的第一个元素m大于右边数组中的某个元素n，
            //那么左边数组中的所有元素都大于n
            count += mid - L + 1;
            help[index++] = nums[R++];
        }else{
            help[index++] = nums[L++];
        }
    }
    while(L <= mid){
        help[index++] = nums[L++];
    }
    while(R <= b){
        help[index++] = nums[R++];
    }

    for(int i = a; i <= b; i++){
        nums[i] = help[i - a];
    }
}

52 两个链表的第一个公共节点

我的解法是先分别计算连个链表的长度，然后让长度较长的那个先遍历几个，直到两个链表剩下的遍历长度相等。

优秀解法：

public static ListNode getIntersectionNode(ListNode headA, ListNode headB) {
    ListNode node1 = headA;
    ListNode node2 = headB;
    while(node1 != node2){
        node1 = node1 != null ? node1.next : headB;
        node2 = node2 != null ? node2.next : headA;
    }
    return node1;
}

node1先指向headA遍历第一个链表，遍历到头再开始遍历第二个链表；

node2先指向headB遍历第二个链表，遍历到头再开始遍历第一个链表。

当node1与node2相等（包括node1与node2都为空）时，node1或node2即为结果

53 在排序数组中查找数字I

使用二分查找，分别找出等于区域的左右边界，然后相减

54 二叉搜索树的第K大节点

morris反向遍历

56 数组中数字出现的次数

一个整型数组 nums 里除两个数字之外，其他数字都出现了两次。请写程序找出这两个只出现一次的数字。

要求时间复杂度是O(n)，空间复杂度是O(1)。

思路：假设数组中两个只出现一次的元素分别为A和B，先将数组中所有数字都异或，得到结果C。则A^B=C

C肯定不为0，则C的二进制表达中肯定有1。使用(c&-c)得到C中最低位为1的值。如何求一个二进制数的最低位的1在哪里？，假设C的二进制最低位为1的为是第二位

划分数组（将nums数组分成两个数组：二进制倒数第二位为1，二进制倒数第二位不为1。这样就把A与B分到了两个数组中）: 从头到尾异或数组中的数字,得到最后结果temp,在temp中至少有一位是1,因为存在两个不相同的数字,找到temp中从又往左的第一个为1的位置的数字num,例如temp = 10,二进制为1010,temp从又往左的第一个为1的位置的数字为num = 10(二进制),我们在通过num和数组中的各个数字分别取异或,这样就将其分成了两个数组,接下来只要分别对两个子数组求异或,就能得到最后的结果了

为了清晰,上个例子:[2,4,3,6,3,2,5,5],当我们遍历异或完成后得到二进制的数字0010,我们根据倒数第二位是不是1将数组分成两个数组,分别为[2,3,6,3,2]和[4,5,5],其中前面数组中数字的第二位都是1,后面数组中数字的第二位都是0,两个数组分别取异或,第一个数组得到6,第二个数组得到4,完成!

    public static int[] singleNumbers(int[] nums) {
        int c = 0;
        for(int i = 0; i < nums.length; i++){
            c ^= nums[i];
        }
        int last = c & (-c);
        int a = 0;
        int b = 0;
        for(int i = 0; i < nums.length; i++){
            if((nums[i] & last) == last){
                a ^= nums[i];
            }else{
                b ^= nums[i];
            }
        }
        return new int[]{a, b};
    }

56_2 数组中数字出现的次数2

以题干给出的示例1为例，nums=[3,4,3,3]，将数组中各个数字采用二进制的方式写出，
3 = （0011）2
4 = （0100）2
3 = （0011）2
3 = （0011）2

通过对数组中各个数的二进制表示形式逐位进行观察，我们可以发现，当数组中只出现一次的那个数字(用k表示)在二进制的对应位为0时，该对应位为1在数组各个数字中出现的总次数应当为3n，当k的对应位为1时，该对应位为1在数组各个数字中出现的总次数应当为3n + 1，为此，我们可以统计数字中的各个位中1出现的次数，当为3n次时，只出现一次的数字的对应位应当为0，当为3n + 1次时，只出现一次的数字的对应位应当为1。由此，我们可以得到如下代码：

public int singleNumber(int[] nums) {
    if(nums == null || nums.length == 0){
        return 0;
    }
    int res = 0;
    int index = 1;
    for(int i = 0; i < 32;i ++){
        int count = 0;
        for(int j = 0; j < nums.length; j++){
            if((nums[j] & index) == index){
                count++;
            }
        }
        if(count % 3 == 1){
            res |= index;
        }
        index = index << 1;
    }
    return res;
}

57 和为s的两个数字

暴力递归超时
使用Set需要O(N)的空间复杂度
使用碰撞双指针

57_2 和为s的连续正数序列

使用滑动窗口，但是需要返回一个二维数组int[][]

先构造一个int[]型的链表lists，然后使用toArray(T[] t)方法转换为数组

本题中

List<int[]> lists = new ArrayList<>();
...
return lists.toArray(new int[lists.size()][]);

传入的参数最好指定二维数组有多少行，如果指定二维数组较小，就会新创建一个数组，将链表中的值复制到这个新数组上，这不就有多于的操作了吗。还不如直接定义好二维数组的大小，转换为数组的时候，直接将链表中的值复制到这个定义好的二维数组上。

深入理解List的toArray()方法和toArray(T[] a)方法

59_1 ***滑动窗口的最大值

好好再做一遍。

class Solution {
    public static int[] maxSlidingWindow(int[] nums, int k) {
        if(nums == null || nums.length == 0){
            return new int[0];
        }
        int len = nums.length - k + 1;
        int[] res = new int[len]; int index = 0;
        //使用双端单调队列，只往队列中放比头结点小的数。
        LinkedList<Integer> queue = new LinkedList<>();
        for(int i = 0; i < nums.length; i++){
            while(!queue.isEmpty() && nums[queue.peekLast()] < nums[i]){
                queue.pollLast();
            }
            queue.addLast(i);
            if(queue.peekFirst() == i - k){
                queue.pollFirst();
            }
            if(i >= k - 1){
                res[index++] = nums[queue.peekFirst()];
            }
        }
        return res;
    }
}

59_2 ***队列中的最大值

和59_1一样，都是用到了单调队列。这两个题要好好做。

60 n个骰子的点数

使用动态规划

package six;

import java.util.Arrays;

public class Solution60 {
    public static double[] twoSum(int n) {

        double SUM = Math.pow(6, n);
        //设F(n,s)为当骰子数为n，和为s的情况数量
        //F(n,s)=F(n?1,s?1)+F(n?1,s?2)+F(n?1,s?3)+F(n?1,s?4)+F(n?1,s?5)+F(n?1,s?6)
        //注意：F(n,s)由不多于6个数相加得到。
        int[][] dp = new int[n + 1][6 * n + 1];
        for(int i = 1; i <= 6; i++){
            dp[1][i] = 1;
        }

        //填充dp表，表中很多位置为0，表示不可能出现这种情况
        //二维矩阵中最后一行从dp[n][n]开始，到dp[n][6*n]结束，分别代表不同和的出现数量
        for(int j = 2; j <= n; j++){
            for(int k = j; k <= j * 6; k++){
                //最多相加6次得到
                for(int q = 1; q <= 6; q++){
                    if(k - q < j - 1){
                        break;
                    }
                    dp[j][k] += dp[j - 1][k - q];
                }
            }
        }
        //总共能出现5*n+1种结果
        double[] res = new double[n * 5 + 1];
        //只遍历dp二维表的最后一行，从dp[n][n]开始
        for(int i = n; i <= 6 * n; i++){
            res[i - n] = dp[n][i] / SUM;
        }
        return res;
    }

    public static void main(String[] args) {
        double[] res = twoSum(2);
        System.out.println(Arrays.toString(res));
    }
}

作者：shy-14
链接：https://leetcode-cn.com/problems/nge-tou-zi-de-dian-shu-lcof/solution/dong-tai-gui-hua-by-shy-14/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

61 扑克牌中的顺子

可以使用两种方式：排序数组和不排序

package seven;

import java.util.Arrays;
import java.util.HashSet;

class Solution{
    public static boolean isStraight(int[] nums){
        //插入排序
        for(int i = 1; i < nums.length; i++){
            int j = i - 1;
            int k = i;
            while(j >= 0 && nums[j] > nums[k]){
                swap(nums, k, j);
                k--;
                j--;
            }
        }
        //统计大小王的数量，测试用例中大小王可能多于两张
        int king = 0;
        for (int num : nums) {
            if (num == 0) {
                king++;
            } else {
                break;
            }
        }
        //遍历排好序的数组，如果遇到两个相邻元素不连续，看能否用剩下的大小王补齐
        for(int i = king; i < nums.length; i++){
            //如果遇到重复元素，直接返回false
            if(i + 1 < nums.length && nums[i + 1] == nums[i]){
                return false;
            }
            if(i + 1 < nums.length && nums[i + 1] - nums[i] > 1){
                if(king > 0){
                    nums[i]++;
                    king--;
                    i--;
                }else{
                    return false;
                }
            }
        }
        return true;
    }
    public static void swap(int[] arr, int a, int b){
        int temp = arr[a];
        arr[a] = arr[b];
        arr[b] = temp;
    }

    //不排序的方式
    public static boolean isStraight2(int[] nums){
        //用于判断数组中是否有重复元素
        HashSet<Integer> set = new HashSet<>();
        int min = Integer.MAX_VALUE;
        int max = Integer.MIN_VALUE;
        for(int num : nums){
            //如果是0，不存入set，直接跳过
            if(num == 0){
                continue;
            }
            //如果存在重复元素，直接false
            if(set.size() > 0 && set.contains(num)){
                return false;
            }else{
                //由于规定数组长度为5
                //如果max与min差值大于4，则不能凑成顺子
                set.add(num);
                min = Math.min(num, min);
                max = Math.max(num, max);
            }
        }
        return max - min <= 5;
    }

    public static void main(String[] args) {
        int[] arr = {11,0,9,0,0};
        System.out.println(isStraight2(arr));
    }
}

62 ***约瑟夫环问题

https://www.jianshu.com/p/eeb696037bfc

可以用数组，但是不要忘记更新索引。

使用数组

//使用数组，不要忘记找到要删除的元素时，更新下标
public static int process1(int n, int m){
    List<Integer> list = new ArrayList<>();
    for(int i = 0; i < n; i++){
        list.add(i);
    }
    int count = 1;
    int index = 0;
    while(list.size() > 1){
        if(count == m){
            System.out.print(list.get(index) + " ");
            list.remove(index);
            index--;
            count = 1;
        }else{
            count++;
        }
        index++;
        if(index >= list.size()){
            index = 0;
        }
    }
    System.out.println();
    return list.get(0);
}

使用自定义的链表

public static class Node{
    int val;
    Node next;
    Node(int val){
        this.val = val;
    }
}

public static int process2(int n, int m){
    Node head = new Node(0);
    Node cur = head;
    for(int i = 1; i < n; i++){
        cur.next = new Node(i);
        cur = cur.next;
    }
    cur.next = head;
    Node pre = cur;
    cur = head;
    int count = 1;
    while(cur.next != cur){
        if(count == 3){
            pre.next = cur.next;
            cur.next = null;
            cur = pre.next;
            count = 1;
        }else{
            pre = cur;
            cur = cur.next;
            count++;
        }
    }
    return cur.val;
}

数学解法

利用数学方法

我们有n个数，下标从0到n-1，然后从index=0开始数，每次数m个数，最后看能剩下谁。我们假设能剩下的数的下标为y，则我们把这件事表示为

f(n,m) = y

这个y到底表示了啥呢？注意，y是下标，所以就意味着你从index=0开始数，数y+1个数，然后就停，停谁身上谁就是结果。

行了，我们假设f(n-1,m)=x，然后来找一找f(n,m)和f(n-1,m)到底啥关系。

f(n-1,m)=x意味着啥呢？意味着有n-1个数的时候从index=0开始数，数x+1个数你就找到这结果了。那我不从index=0开始数呢？比如我从index=i开始数？那很简单，你把上面的答案也往后挪i下，就得到答案了。当然了，你要是挪到末尾了你就取个余，从头接着挪。

于是我们来思考f(n,m)时考虑以下两件事：

有n个数的时候，要划掉一个数，然后就剩n-1个数了呗，那划掉的这个数，下标是多少？
划完了这个数，往后数，数x+1个数，停在谁身上谁就是我们的答案。当然了，数的过程中你得取余

问题一：有n个数的时候，划掉了谁？下标是多少？

因为要从0数m个数，那最后肯定落到了下标为m-1的数身上了，但这个下标可能超过我们有的最大下标（n-1）了。所以攒满n个就归零接着数，逢n归零，所以要模n。

所以有n个数的时候，我们划掉了下标为(m-1)%n的数字。

问题二：我们划完了这个数，往后数x+1下，能落到谁身上呢，它的下标是几？

你往后数x+1，它下标肯定变成了(m-1)%n +x+1，和第一步的想法一样，你肯定还是得取模，所以答案为[(m-1)%n+x+1]%n，则

f(n,m)=[(m-1)%n+x+1]%n

其中x=f(n-1,m)

我们化简它！

定理一：两个正整数a，b的和，模另外一个数c，就等于它俩分别模c，模完之后加起来再模。

(a+b)%c=((a%c)+(b%c))%c

定理二：一个正整数a，模c，模一遍和模两遍是一样的。

a%c=(a%c)%c

你稍微一琢磨就觉得，嗯，说得对。

所以

f(n,m)=[(m-1)%n+x+1]%n
	  =(m-1)%n%n+(x+1)%n
      =(m-1)%n+(x+1)%n
      =[(m-1)+(x+1)]%n
      =(m-1+x+1)%n
      =(m+x)%n

其中，x=f(n-1,m)
所以，f(n,m) = (f(n-1, m) + m) %n，得到的结果为最后剩下的那个数的下标

//总共有n个人，第m个人出列，求最后剩下的那个人的下标
public static int process(int n, int m){
    if(n == 1) return 0;
    int temp = (process(n - 1, m) + m) % n;
    System.out.println("当n为"+n + "时,最后剩下的那个数为"+temp);
    return temp;
}

63 股票的最大利润

使用动态规划更简单

65 使用位运算实现两数相加

作者：ccav
链接：https://leetcode-cn.com/problems/bu-yong-jia-jian-cheng-chu-zuo-jia-fa-lcof/solution/er-jin-zhi-qiu-he-chao-xiang-xi-da-bai-10000yong-h/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。