[数据结构与算法]Java学习 day28_tree

BStree

tree的一些基本概念

1.1 树的定义

与线性表表示的一一对应的线性关系不同，树表示的是数据元素之间更为复杂的非线性关系。 直观来看，树是以分支关系定义的层次结构。

简单来说，树表示的是1对多的关系。
树的定义（逻辑结构）： 树(Tree)是n( n>=0 )个结点的有限集合，没有结点的树称为空树，在任意一颗非空树中： 有且仅有一个特定的称为根(root)的结点 当n>1的时，其余结点可分为 m( m>0 ) 个互不相交的有限集T1，T2，…, Tm，其中每一个集合 Ti 本身又是一棵树，并且称之为根的子树。

注意：树的定义是一个递归定义，即在树的定义中又用到树的概念。

二叉树
如果树的节点是i，那么左孩子的节点是2i，右孩子的节点是2i+1

自己实现一个BStree

package BStree;

import java.util.ArrayList;
import java.util.Deque;
import java.util.LinkedList;
import java.util.List;

/**
 * 2, 实现前序遍历(栈实现  和  递归实现)
 *
 * 3, 根据前序和中序实现建树操作
 */

/**
 *  1, 集合类:  数据容器
 *  2, 底层结构:  链表
 *  3, 表示数据结构: 二叉搜索树,   (二叉,   有大小)
 *  // 因为二叉搜索树, 是对结点存储的值, 需要比较大小的
 *  // 也就意味着存储到二叉搜索树上的内容, 要可以比较大小
 */

public class MyBSTree < T extends Comparable<T>> {

    private Node root; // 二叉搜索树的根节点
    private  int size;

    // 对二叉搜索树的添加方法: 在二叉搜索树种添加一个结点/值
    public boolean add(T value) {

        if(value == null)  throw new IllegalArgumentException("param can not be  null");

        if(isEmpty()){
            // 树为空，新元素作为新节点
            root = new Node(value, null, null);
            size++;
            return true;
        }

        // 树不空，按照大小查找比较
        Node mid = root;
        Node midF = null; // 保存遍历节点的父节点
        int com = 0;
        while(mid != null){
            com = value.compareTo(mid.value);
            midF = mid;  // midF是要添加位置的父节点
            if(com > 0){

                mid = mid.right;

            }else if(com < 0){

                mid = mid.left;
            }else return false;
        }

        if(com > 0){
            // 最后一次比较，com大
            midF.right = new Node(value, null, null);
        }else {
            midF.left = new Node(value, null, null);
        }
        size++;

        return true;
    }



    // 对二叉搜索树的删除方法: 在二叉搜索树中删除一个结点值
    public boolean remove(T value) {
        if(value == null)  throw new IllegalArgumentException("param can not be  null");
        if(isEmpty()) throw new RuntimeException("tree is empty");

        Node mid = root; //用于查找要删除节点
        Node midF = null;
        int com = 0;
        while (mid != null){
            com = value.compareTo(mid.value);
            if(com == 0){
                break;
                //找到了要删除的节点就退出循环

            }else if(com > 0){
                midF = mid;
                mid = mid.right;

            }else {
                midF = mid;
                mid = mid.left;
            }
        }

        // 上述循环有两个退出条件， 一个是mid==null，说明没找到
        // 否则是找到了
        if(mid == null) return false;

        // mid就是要删除的节点位置，midF是要删除节点的父位置
        // 先处理双分支的情况，代码可以复用

        if(mid.left != null && mid.right != null){
            // 可以选左子树最大或者右子树的最小值，这里选择右子树的最小值
            Node min = mid.right;
            Node minF = mid;
            while (min.left != null){
                minF = min;
                min = min.left;
            }
            mid.value = min.value;
            mid = min;
            midF = minF;
        }

        // 如果是从上面的if中出来的，肯定是没有left的，但是可能要删除的节点只有一边，下面的语句就是处理这种情况
        Node ch = mid.left != null ? mid.left : mid.right;

        // 删除是root 的情况
        if(midF == null){
            root = ch;
            size--;
            return true;
        }

        if(mid == midF.left){
            midF.left = ch;
        }else {
            midF.right = ch;
        }
        size--;


        return true;
    }


    // 查找二叉搜索树中, 某个值是否存在
    public boolean contains(T value){
        if(value == null)  throw new IllegalArgumentException("param can not be  null");
        if(isEmpty()) throw new RuntimeException("tree is empty");

        Node mid = root;
        while (mid != null){
            int com = value.compareTo(mid.value);

            if(com == 0){
                return true;
            }else if(com > 0){
                mid = mid.right;
            }else {
                mid = mid.left;
            }
        }

        return false;
    }


    public List<T> postOrder(){

        LinkedList<T> list = new LinkedList<>();
        if(isEmpty()) return list;
        Deque<Node> stack = new LinkedList<>();

        stack.push(root);

        while (!stack.isEmpty()){

            Node x = stack.pop();

            // 头插法，后出栈的会被放到链表头部
            list.addFirst(x.value);

            if(x.left != null) stack.push(x.left);
            if(x.right != null) stack.push(x.right);
        }

        return list;

    }


    public List<T> postOrderRecursion(){
        ArrayList<T> list = new ArrayList<>();
        postOrderRecursion(root, list);
        return list;
    }


    private void postOrderRecursion(Node root, ArrayList<T> list){
        if(root == null) return;

        postOrderRecursion(root.left, list);
        postOrderRecursion(root.right, list);

        list.add(root.value);
    }


    // 前序
    public List<T> inOrder(){

        LinkedList<T> list = new LinkedList<>();
        Deque<Node> stack = new LinkedList<>();
        Node mid = root;

        while(!stack.isEmpty() || mid != null){
            while (mid != null){
                stack.push(mid);
                mid = mid.left;
            }
            mid = stack.pop();
            list.add(mid.value);

            mid = mid.right;
        }

        return list;
    }


    public List<T> inOrderRecursion(){
        ArrayList<T> list = new ArrayList<>();
        inOrderRecursion(root, list);
        return list;
    }

    private void inOrderRecursion(Node root, ArrayList<T> list){
        if(root == null) return;

        inOrderRecursion(root.left, list);
        list.add(root.value);
        inOrderRecursion(root.right, list);
    }


    public List<T> preOrder(){
        LinkedList<T> list = new LinkedList<>();
        Deque<Node> stack = new LinkedList<>();
        Node mid = root;
         stack.push(mid);
        while(!stack.isEmpty() && mid != null){
            mid = stack.pop();
            list.add(mid.value);
            if(mid.right != null) stack.push(mid.right);
            if(mid.left != null) stack.push(mid.left);
        }

        return list;
    }

    public List<T> preOrderRecursion(){
        ArrayList<T> list = new ArrayList<>();
        preOrderRecursion(root, list);
        return list;

    }

    private void preOrderRecursion(Node root, ArrayList<T> list){
        if(root == null) return;
        list.add(root.value);

        preOrderRecursion(root.left, list);
        preOrderRecursion(root.right, list);
    }


    // 层级遍历: 队列

    // 建树操作: 前序+中序
    // 建树操作: 后序+中序


    public void byPostAndInorder(List<T> postOrder, List<T> inOrder){
        root = byPostAndInorder2(postOrder, inOrder);
        size = inOrder.size();
    }

    private Node byPostAndInorder2(List<T> postOrder, List<T> inOrder) {

        if(postOrder.isEmpty()) return null;
        if(postOrder.size() == 1) return new Node(postOrder.get(0));

        // 根节点是后序的最后一个元素
        T rootValue = postOrder.get(postOrder.size() - 1);
        int index = inOrder.indexOf(rootValue);
        Node node = new Node(rootValue, null, null);

        List<T> inleft = inOrder.subList(0, index);
        List<T> inRight = inOrder.subList(index+1, inOrder.size());
        List<T> postLeft = postOrder.subList(0, index);
        List<T> postRight = postOrder.subList(index, inOrder.size()-1);

        node.left = byPostAndInorder2(postLeft, inleft);
        node.right = byPostAndInorder2(postRight, inRight);
        return node;
    }


    public void byPreAndInorder(List<T> preOrder, List<T> inOrder){
        root = byPreAndInorder2(preOrder, inOrder);
        size = inOrder.size();
    }

    private Node byPreAndInorder2(List<T> preOrder, List<T> inOrder) {

        if(preOrder.isEmpty()) return null;
        if(preOrder.size() == 1) return new Node(preOrder.get(0));

        // 根节点是前序的第一个元素
        T rootValue = preOrder.get(0);
        int index = inOrder.indexOf(rootValue);
        Node node = new Node(rootValue, null, null);

        List<T> inleft = inOrder.subList(0, index);
        List<T> inRight = inOrder.subList(index+1, inOrder.size());
        List<T> preLeft = preOrder.subList(1, index+1);
        List<T> preRight = preOrder.subList(index+1, inOrder.size());

        node.left = byPreAndInorder2(preLeft, inleft);
        node.right = byPreAndInorder2(preRight, inRight);
        return node;
    }

    public boolean isEmpty(){
        return size == 0;
    }
    public int size(){
        return size;
    }
    // --------------------------------------------------
    // 前序: 栈, 递归
    // 中序: 栈, 递归
    // 后序: 栈, 递归

    //-----------------------------------------------

    class Node {
        T value;
        Node left;
        Node right;
        public Node(T value) {
            this.value = value;
        }

        public Node(T value, Node left, Node right) {
            this.value = value;
            this.left = left;
            this.right = right;
        }
    }
}

2-3-4树

在讲红黑树之前，作为引入，学习一下2-3-4树

节点类型：

每个结点可以拥有1, 2, 或者3个键。

• 2-node：1个键，2个孩子
• 3-node：2个键，3个孩子
• 4-node：3个键，4个孩子

查找

查找很简单，按照树本身划分的区间逐步查找就行

插入

2-3-4树的插入，不会直接插入一个新的节点，新节点永远是和已经存在的节点凑在一起，只有分裂可以产生新节点
插入B，2-node变成3-node

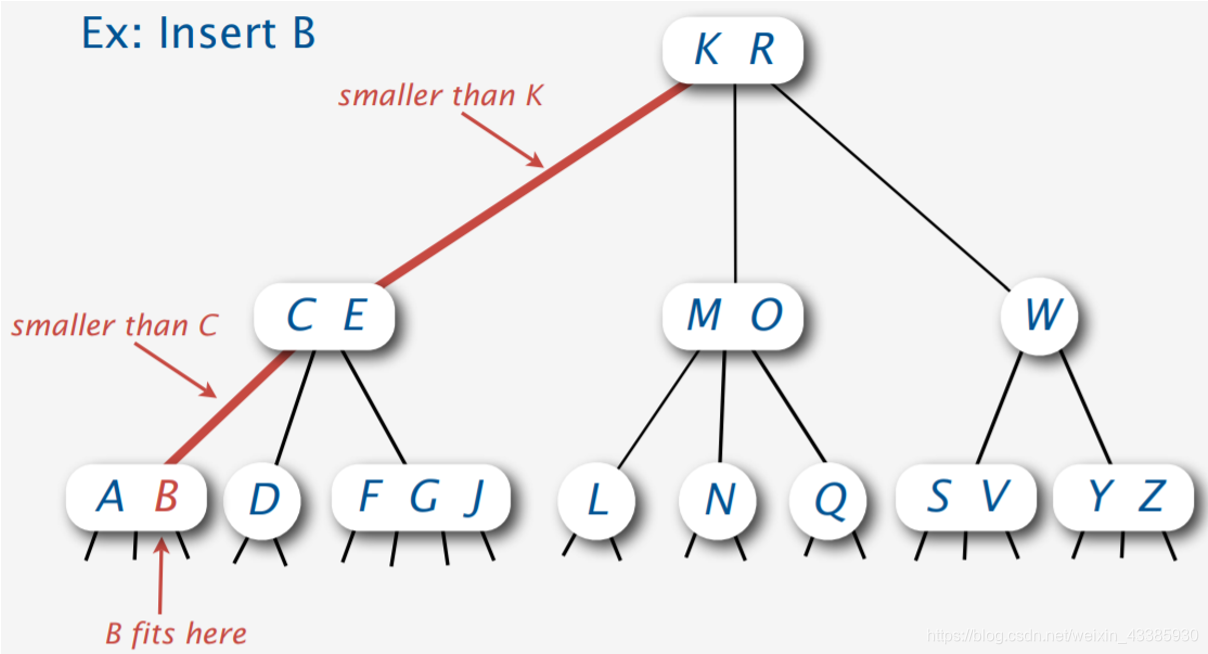
插入X，3-node变为4-node

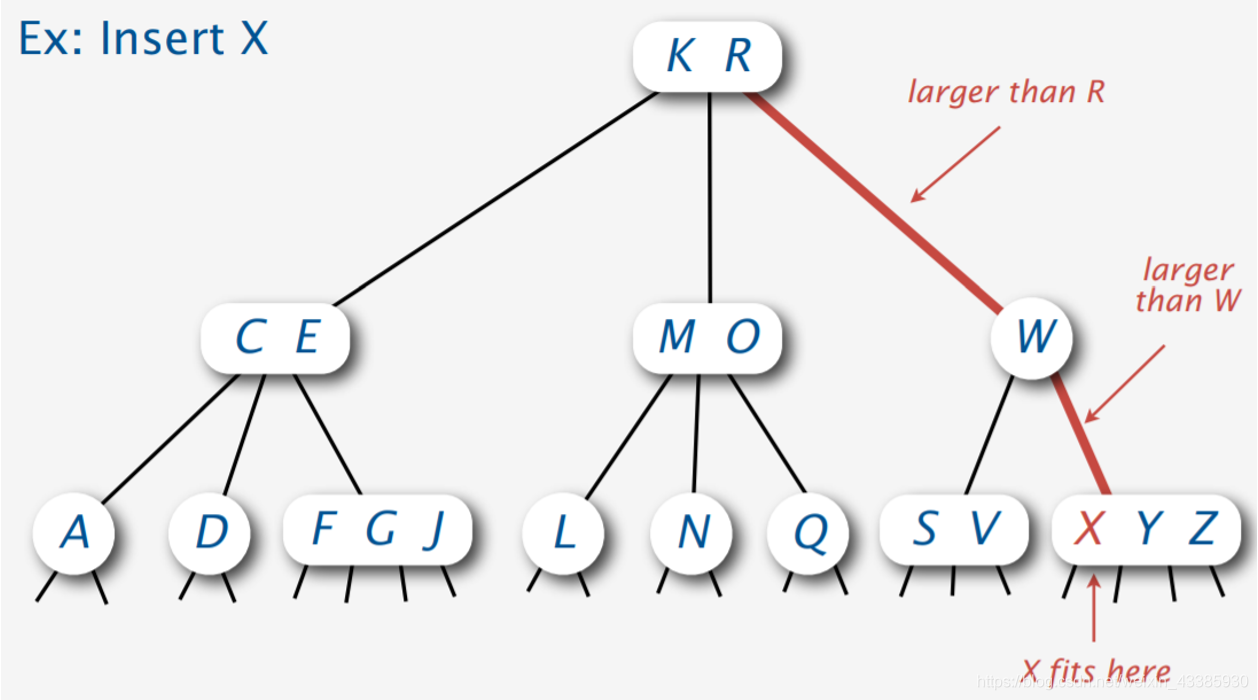
插入H，底部没有位置给H，必须进行节点的分裂

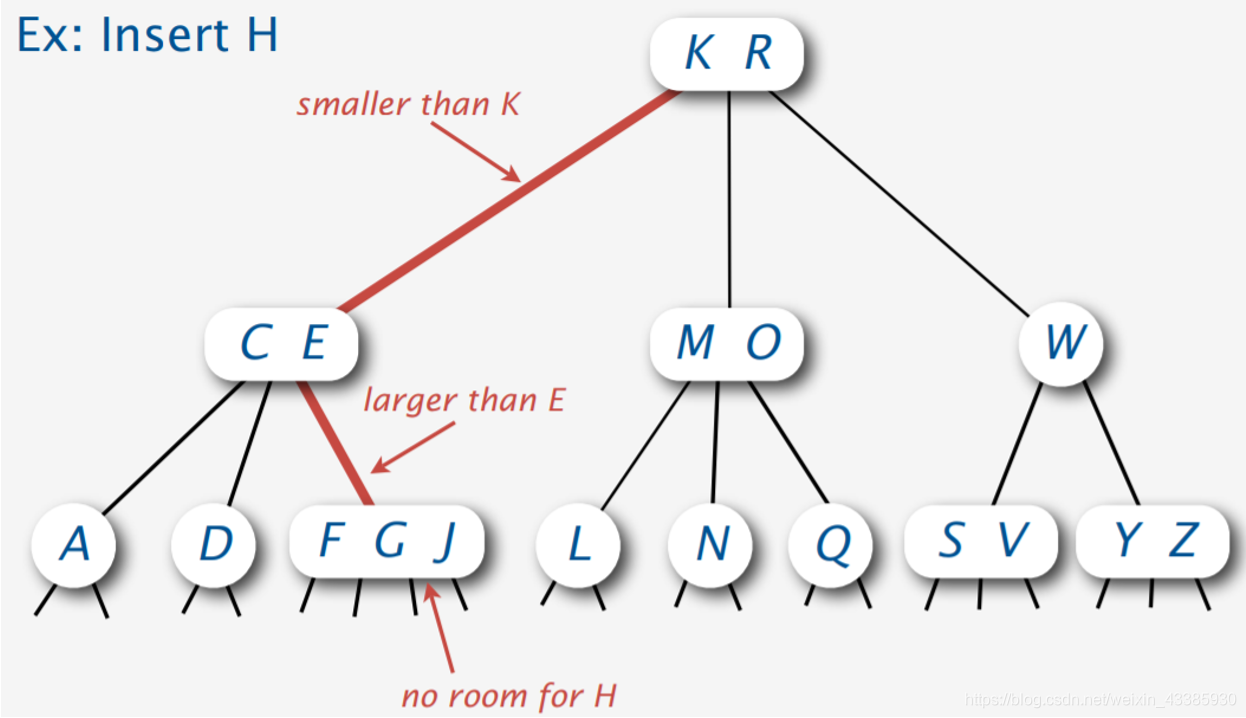
节点分裂：

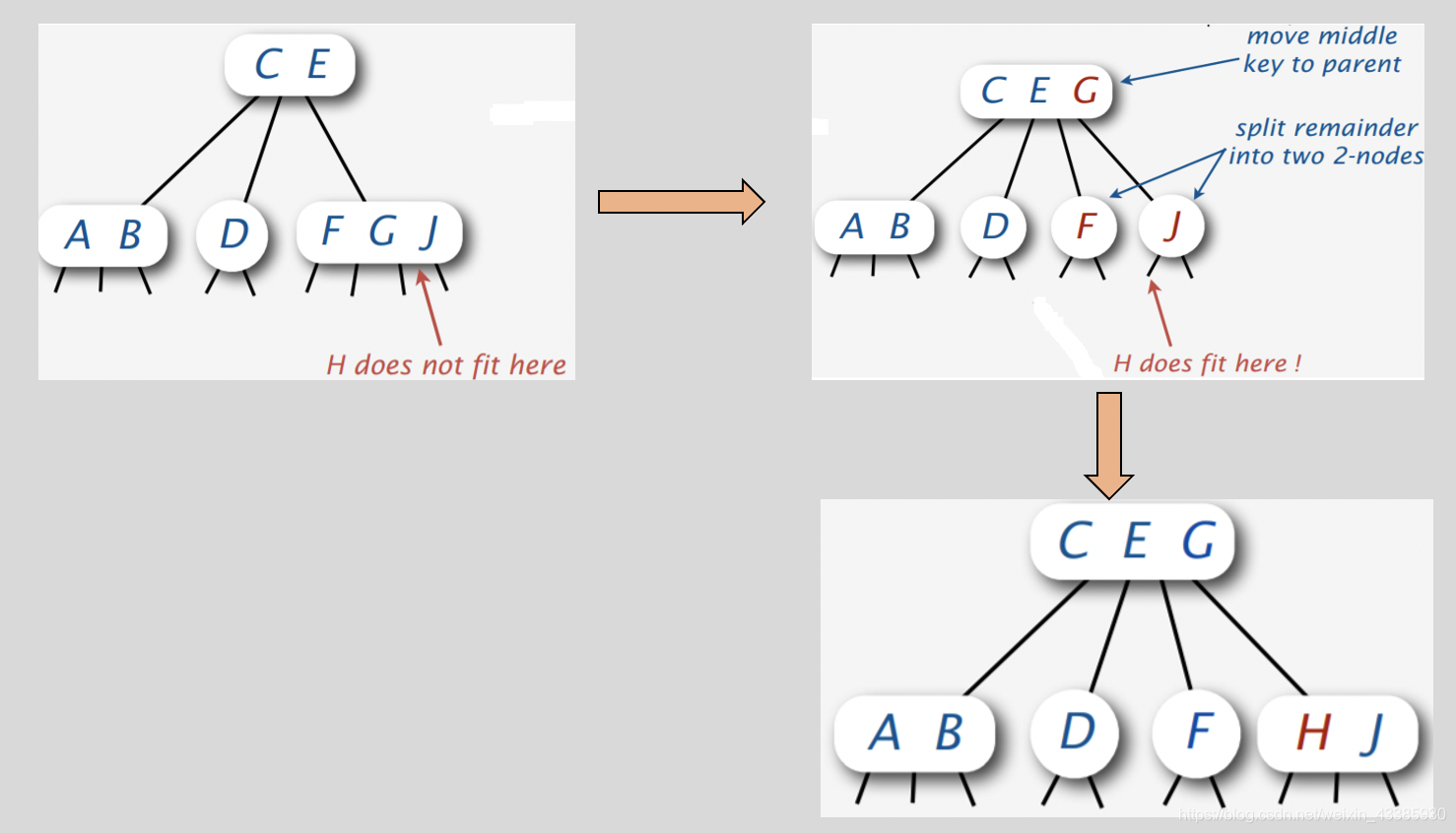
当然，这也引入了一个问题，如果父节点也是4-Node的时候，没办法进行分裂，这就要Top-Down方法

Top-Down方法
确保当前节点4-node，预留空间给新元素（也就是说，在向下查找的过程中，你遇到了下述的情况，不管会不会在这里插入，都先给分裂了）

• 沿着查找路径向下分裂4-node
• 在底部插入新元素

• 局部变换只会影响局部的布局，不会影响更大的整体
  

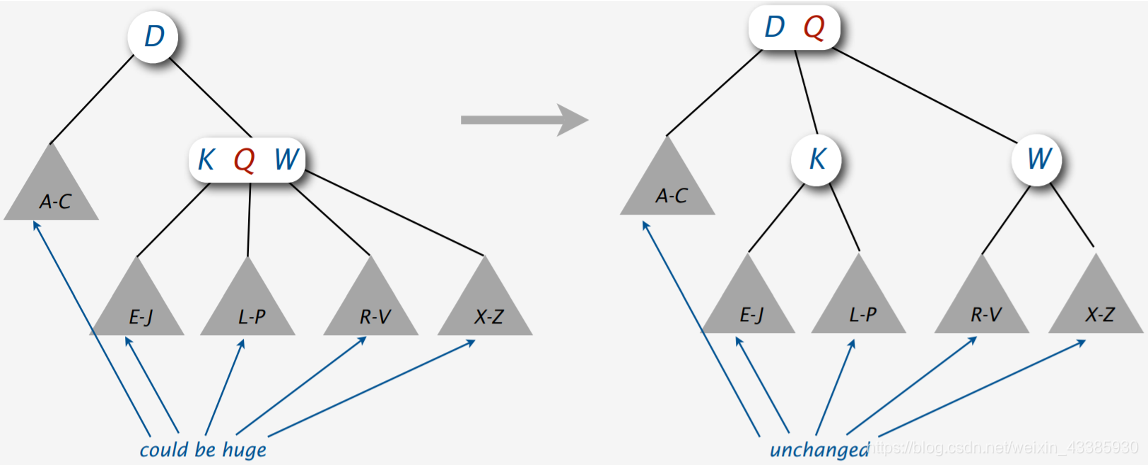
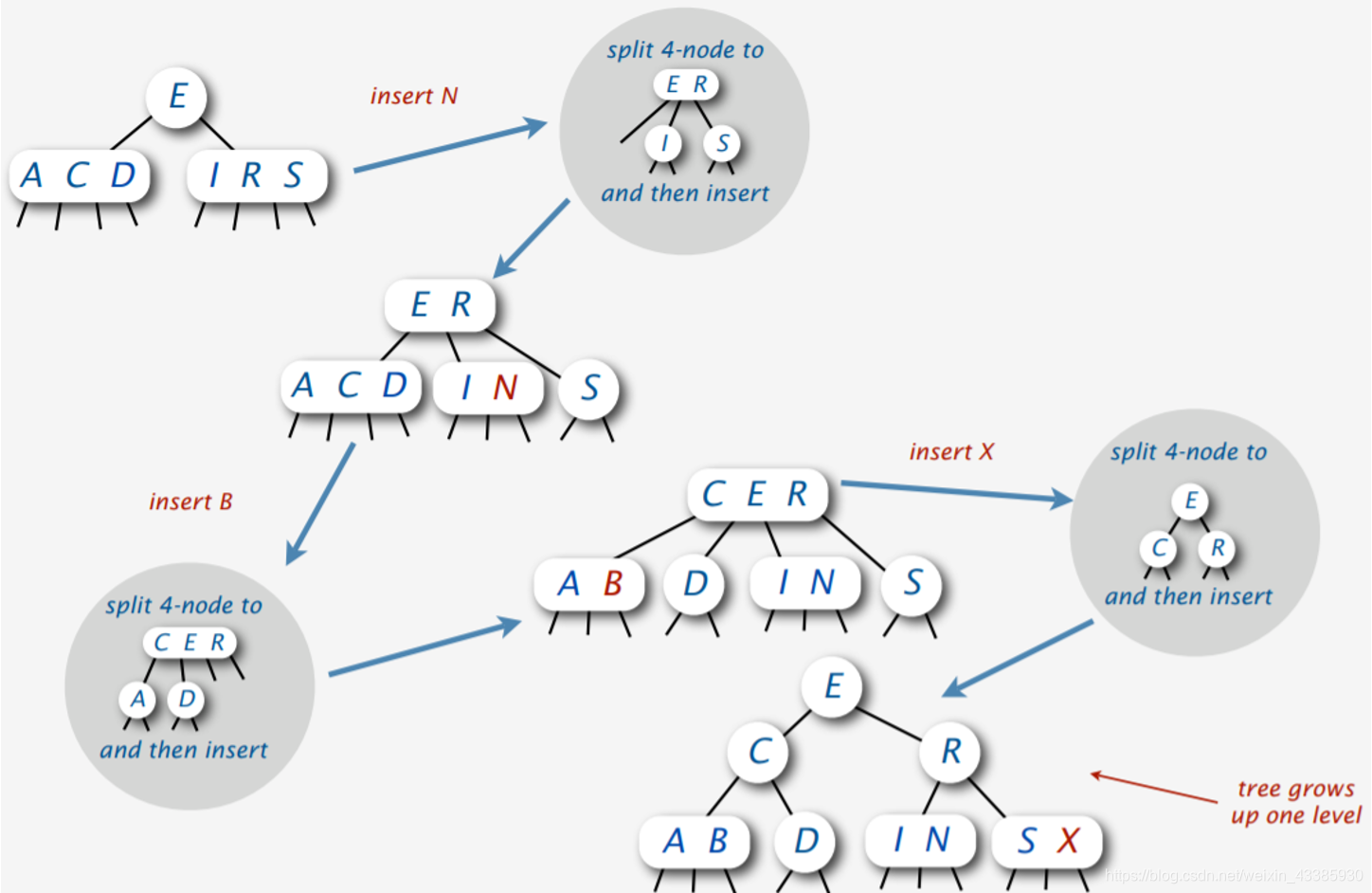
最后插入X的时候，路过了4-node，根据语法也会将其转化，虽然直接插入也没有问题

2-3-4树的性能分析

树的高度
最坏情况: lg N [全部是2-node]
最好情况: log4N = ? lg N [全部是4-node]
100万个结点高度在[10, 20]
10亿个结点高度在[15, 30]

• 2-3-4树保证了树的高度为 O(lgN) !

1 红黑树

数据结构:
集合
线性表( 栈 和 队列 )
树, (普通的树, 二叉树, 二叉搜索树)
图

我们频繁的对二叉搜索树进行添加和删除, 有可能导致二叉搜索树变成一个稀疏树,

为了解决上述问题, 产生了一个:
自平衡的二叉搜索树: 二叉搜索树的一个升级版本
自平衡的二叉搜索树: 在二叉搜索树的基础上, 要求树中每一个结点, 左右子树的高度相差不能超过1

红黑树极类似于自平衡的二叉搜索树, 但是 红黑树不是自平衡的二叉搜索树, 红黑树是一个特殊的二叉搜索树, 也能保证平衡(实际平衡的程度不如自平衡的二叉搜索树平衡)

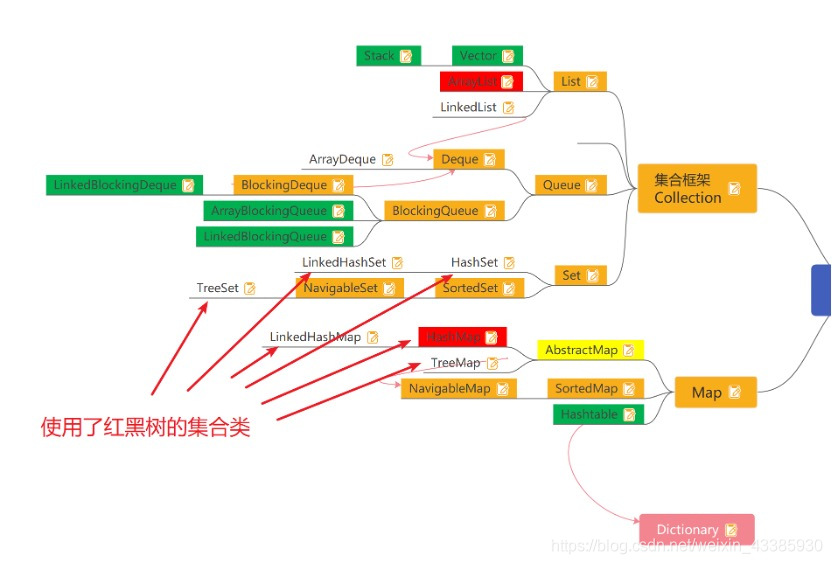
学习红黑树: 了解
什么是红黑树? 红黑树有哪些特点? 红黑树怎么保证的黑高平衡? 红黑树再java中哪些集合类中使用? 为什么在这个地方使用红黑树? 什么时候用的?

2-3-4树

2.1 什么是2-3-4树

2-3-4树是在普通的二叉查找树上进行了扩展，它允许有多个键(1~3个) 树保持完美平衡 完美平衡？根到每个叶子结点的路径都是一样长。(所有的叶子都在同一层级上)
每个结点可以拥有1, 2, 或者3个键。 2-node(2结点)：1个键，两个孩子 3-node(3结点)：2个键，三个孩子 4-node(4结点)：3个键，四个孩子

2.2 查找操作

2.3 添加操作

添加的元素, 永远是和别的已经存在的结点共同构建成同一个结点

在2-3-4树添加过程中, 为了避免最后添加的时候, 需要向上分裂, 当时上面父元素没有位置可分裂(父元素也需要向它自己的父元素分裂), 为了避免这种麻烦的情况出现, 所以在添加的时候, 我们一般保证, 添加的过程中,遇到四结点(3 key) 先向上分裂(即使最终不需要分裂)

2.4 删除操作

3 红黑树

算法导论中关于红黑树的定义： 一棵红黑树是满足下面红黑性质的二叉搜索树： 每个结点或者是红色的，或者是黑色的 根结点是黑色的 叶结点 (Nil) 是黑色的 如果一个结点是红色的，则它的两个子结点都是黑色的 （4-node 只有一种编码方式） 对每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点。(黑高平衡， 2-3-4树是一个完美平衡的树)