[数据结构与算法]用堆实现优先级队列

堆的数据结构

堆是一颗二叉树 T ，树在它的位置（节点）上存储了集合中的元组并且满足两个附加的属性：关系属性以存储键的形式在T中定义；结构属性以树 T 自身形状的方式定义

关系属性如下：
Heap-Order是属性： 在堆 T 中，对于除了根的每个位置 p ，存储在 p 中的键值大于或等于存储在 p 的父亲节点的键值。
作为 Heap-Order 属性的结果，T 中从根到叶子的路径上的键值是以非递减顺序排列的，即一个最小的键总是储存在 T de 根节点中。因此调用 min 或 remove_min 时，能够容易地定位这样的元组，一般情况下就在 堆的顶部。

由于效率的原因，堆T 的高度应尽可能小。通过坚持让堆 T 满足结构属性中的附加属性——必须是完全二叉树——来强制满足让堆的高度尽可能小这一需求

堆的高度： 若堆有 n 个元组，则它的高度 h = ?log n?

用堆实现优先级队列

为了实现add(k,v)，在堆中增加一个元组，分为两步：

1. 把键值对作为元组存储树的新节点中。
   为了维持完全二叉树属性，这个新节点 p 应该放在树底层最右节点相邻的位置。如果树的底层已满（或堆为空），则应存放在新一层的最左位置上
2. 插入元组后向上冒泡
   为了保证堆的 heap-order 属性，将 p 位置上的键值与 p 的父节点 q 上的键值进行比较。
   若 $k_p\ge k_q$，则满足 heap-order 属性且算法终止。
   若$k_p<k_q$, 则需要重新调整树以满足 heap-order属性，通过调换存储在位置 p 和 位置 q 的元组来实现。这次交换导致新元组的层次上移一层，重复此操作，直到满足heap-order属性

为了实现 remove_min()，删除键值最小的元组。

1. 获取根节点 r 的元组，将堆T 底层最右位置 p 上的元组复制到根节点 r，删除最后位置的节点 p
2. 保证heap-order 属性。如果 T 只有一个节点，算法终止。否则将 p 初始化 T 的根
   1）如果 p 没有右孩子，令 c 表示 p 的左孩子
   2）否则（p 有两个孩子），令 c 作为 p 的具有较小键值的孩子
   若 $k_p\le k_c$，则 heap-order属性以满足，算法终止。
   若 $k_p>k_c$，则需要重新调整元组的位置来满足heap-order属性。可以通过交换存储在 p 和 c的元组来获得局部满足heap-order属性。继续向下交换直到没有违反 heap-order 属性，这个过程称为堆向下冒泡。在最坏的情况下，堆会一直下移到最底层，remove_min的交换次数等于堆 T 的高度，最大值为?log n?。

基于数组的完全二叉树表示

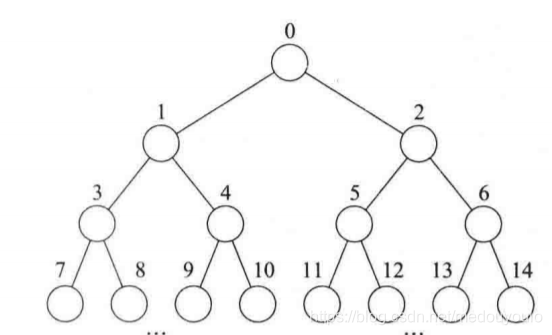
基于数组的二叉树表示非常适合二叉树 T , T的元组被存储在基于数组的列表 A 中，存储在 T 中位置 p 的元素的索引等于层数 f§ ， f§是 p 的函数，其定义如下：

• 若 p 是 T 的根节点，则 f(p) = 0
• 若 p 是位置 q 的左孩子，则 f(p) = 2f(q) + 1
• 若 p 是位置 q 的右孩子，则 f(p) = 2f(q) + 2

Python 的堆实现

使用基于数组的表示，相关变量是整数索引（而不是“位置”对象），采用递归来实现 _upheap 和 _downheap 的重复调用

class HeapPriorityQueue(PriorityQueueBase):
  """ A min-orieented priority queue implented with a binary heap"""
  # -----------nonpublic behaviors-----------------#
  def _parent(self, j):
    return (j-1)//2

  def _left(self, j):
    return 2*j + 1

  def _right(self, j):
    return 2*j + 2

  def _has_left(self, j):
    return self._left(j) < len(self._data)

  def _has_right(self, j):
    return self._right(j) < len(self._data)

  def _swap(self, i, j):
    """Swap the elements at indices i and j of array."""
    self._data[i],self._data[j] = self._data[j],self._data[i]

  def _upheap(self, j):
    parent = self._parent(j)
    if j > 0 and self._data[j] < self._data[parent]:
      self._swap(j, parent)
      self._upheap(parent)

  def _downheap(self, j):
    if self._has_left(j):
      left = self._left(j)
      small_child = left
      if self._has_right(j):
        right = self._right(j)
        if self._data[right] < self._data[left]:
          small_child = right
        if self._data[small_child] < self._data[j]:
          self._swap(j, small_child)
          self._down_heap(small_child) 

#--------------public behaviors--------------#
  def __init__(self):
    """ Create a new empty Priority Queue."""
    self._data = []

  def __len__(self):
    return len(self._data)

  def add(self, key, alue):
    self._data.append(self._item(key, value))
    self._upheap(len(self._data) - 1)

  def min(self):
    if self.is_empty():
      raise Empty('Priority queue is empty')
    item = self._data[0]
    return (item._key, item._value)

  def remove_min(self):
    if self.is_empty():
      raise Empty('Priority queue is empty')
    self._swap(0, len(self._data) - 1)
    item = self._data.pop()
    self._downheap(0)
    return (item._key, item._value)