[数据结构与算法]数据结构 第三、四讲 树(上、中) 笔记

数据结构 第三讲 树 笔记

一、查找

查找：根据某个给定关键字K，从集合R中找出关键字与K相同的记录

静态查找：集合中记录是固定的，没有插入和删除操作，只有查找(查字典)

动态查找：集合中记录是动态变化的，除查找，还可能发生插入和删除

哨兵：在边界处放置，当循环进行至哨兵元素时退出，可以少写一些分支条件(i>0)，是查找的一个技巧

二分查找

int binarysearch(int a[],int x)
{
    int l = 1,r = a.size();
    while(l<=r)
    {
        int mid = (l+r)/2;
        if(x<a[mid]) r = mid;
        else l = mid+1;
        else return mid;
    }
    return NotFound;
}

二、树

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kNle1oAU-1623760132574)(数据结构 第三讲 树 笔记.assets/20210615202647473.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-l0n0cpff-1623760132575)(数据结构 第三讲 树 笔记.assets/20210615202747200.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KxhqvBbM-1623760132577)(C:\Users\ZJQ\AppData\Roaming\Typora\typora-user-images\image-20210613140446435.png)]

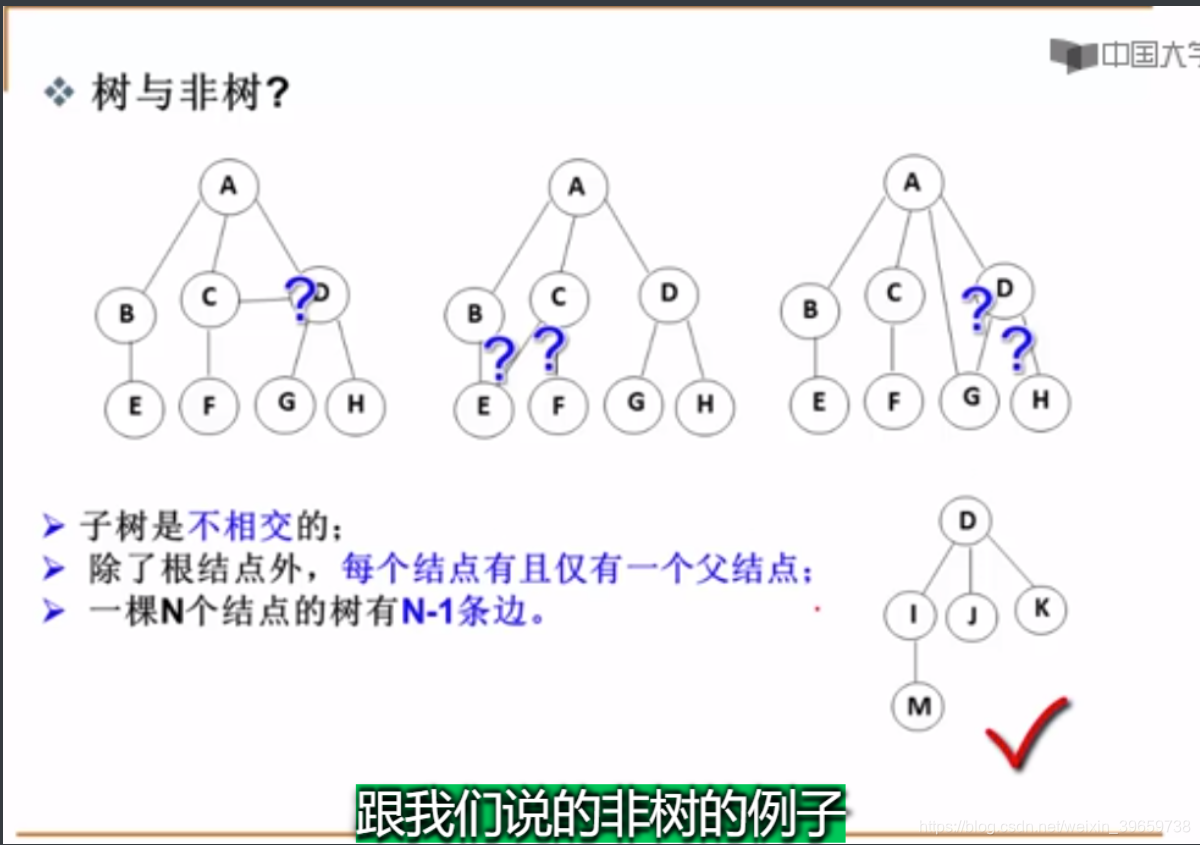
图一：多了一根C.D之间的连线

图二：多了一根C.E之间的连线

图三：多了一根D.G之间的连线

一颗N个结点的树有N-1个边：因为除了根结点，每个结点都有向上的一条边。

解析：m棵树说明有m个根结点，边数 = 结点数 - 根结点数 故为k + m

树是保证结点联通的最小的一种连接方式（因为任意拿走一条边，结点将不会连在一起）

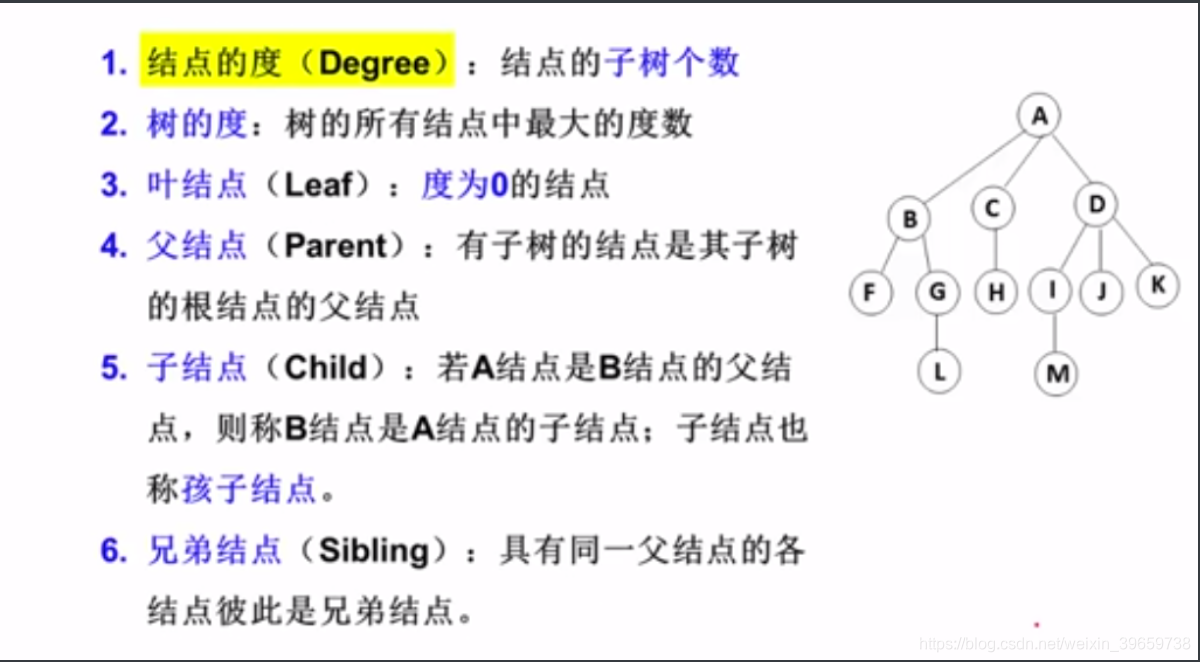
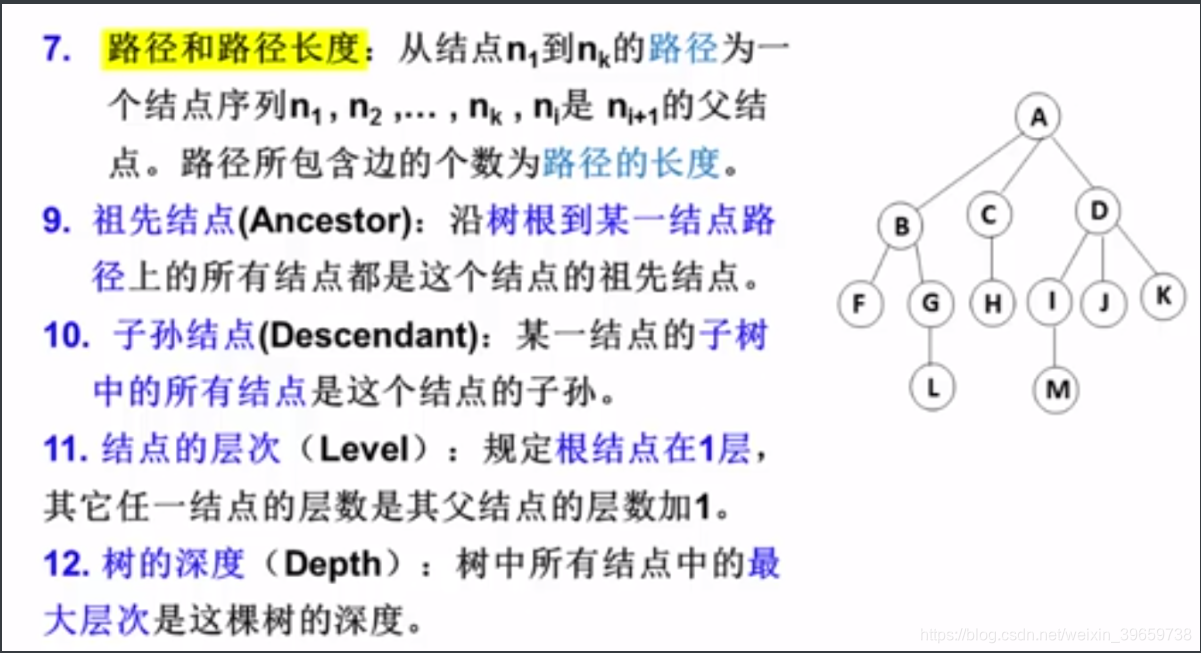
树的一些基本术语

树的表示

n个结点，2n个指针域，其中有n-1条边，说明真正空的域有n+1个

讨论3.2 森林及表示 树的集合称为森林。是否也可以使用“儿子-兄弟”表示法存储森林？如何实现？

A : 法1：增加一个虚拟根结点，作为所有树的根结点的父结点

? 法2：使用“儿子—兄弟”表示法，根结点的兄弟指针域用作连接森林中不同树根结点的指针，森林入口就是最左侧树的根结点

思考题

现在考虑儿子/兄弟表示法，把n个结点串联起来，因为每个结点都有两个部分组成，一个是指向下一个兄弟结点，一个是指向子结点，所以在树中，这两个部分都是需要作为一个单位（即链）来存储的，加上n个结点本身，一共需要3n个空间。

三、二叉树

二叉树T：一个有穷的结点集合。集合可以为空，若不为空，则它是由根结点和称为其左子树TL和右子树TR的两个不相交的二叉树组成。

二叉树的具体五种基本形态

二叉树与度为2的树的区别在于：二叉树的子树有左右顺序之分

特殊二叉树

1.斜二叉树：所有结点只有左儿子（或右儿子），都往一边倒

2.完美二叉树（满二叉树）：除了叶结点，每个结点都有左右儿子，且叶结点都在同一层

3.完全二叉树：对树中结点从上至下，从左至右顺序进行编号。编号为为i（1-n）结点与满二叉树中编号为i结点在二叉树中位置相同（允许最后一层右边有缺少，其余与满二叉树必须一致）

二叉树几个主要性质

1.二叉树第i层最多有2^(i-1)个结点(i>=1)

2.深度为K的二叉树最多有2^k - 1个结点，k >= 1(满二叉树)

3.对任何非空二叉树，度为0的结点总是比度为2的结点多一个

证明：边数 = 结点数 - 1 = n0+n1+n2 - 1 = n0 * 0 + n1 * 1 + n2*2 化简得：n0 = n2 + 1

解释：从上往下看，度为0的结点对边数没有贡献，度为1的结点有一条边，度为2的结点有两条边

二叉树的抽象数据类型定义

常见的遍历方法

讨论3.3 m叉树中各类结点数之间的关系

在二叉树中，我们知道叶结点总数与有两个儿子的结点总数之间的关系是：.

那么类似关系是否可以推广到m叉树中？也就是，如果在m叉树中，叶结点总数是，有一个儿子的结点总数是，有2个儿子的结点总数是，有3个儿子的结点总数是，…。那么，之间存在什么关系？

结点总数 = n0+n1+…+nm

总边数 = n0 * 0 + n1 * 1 + n2 * 2 + …+ nm * m

结点总数 = 总边数 + 1

即 n0+n1+n2+ … +nm = = n0 * 0 + n1 * 1 + n2 * 2 + …+ nm * m + 1

得 n0 = n2 + n3 * 2 +…+nm * (m - 1) + 1

二叉树的存储结构

1.顺序存储结构

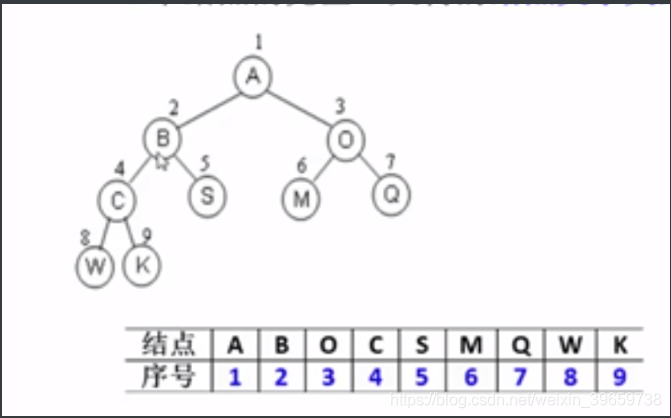
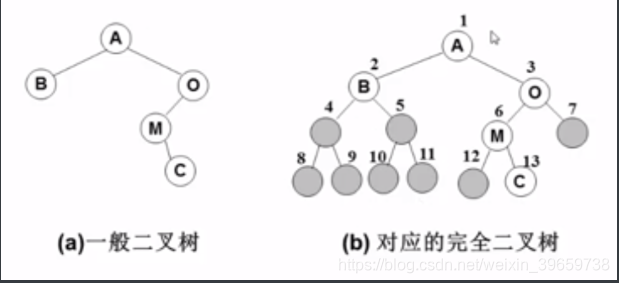
完全二叉树：按从上至下、从左至右顺序存储n个结点的完全二叉树的结点父子关系：

• 非根节点（序号i>1)的父节点的序号是i/2

• 结点（序号为i）的左孩子结点的序号是2i，右孩子结点的序号是2i+1（若n<2i，说明左孩子不存在，n<2i+1，说明右孩子不存在）

  一般二叉树也可以采用这种结构，但会造成空间浪费……

  

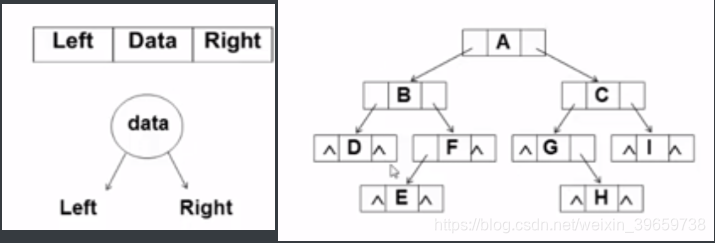
2.链表存储

typedef struct TreeNode *BinTree;
typedef BinTree Position;
struct TreeNode{
    ElementType Data;
    BinTree Left;
    BinTree Right;
}

思考题

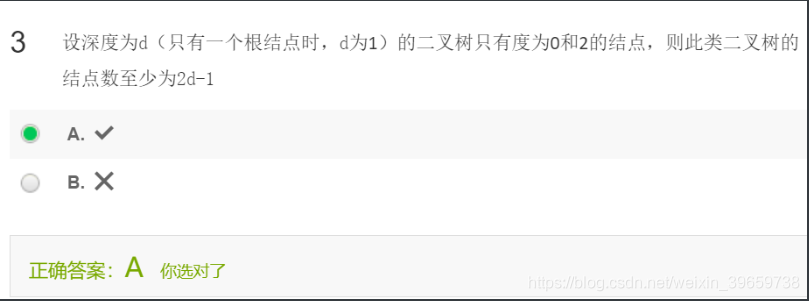
d为1的时候，至少有1个，2 * 1 -1
d为2的时候，没有度为1的点，情况为
o
/ \
o o
至少为3个 = 2 * 2 -1
d大于2的时候，由于没有度为1的点，所以每增加一层，每层至少增加两个，至少的情况是增加2个
所以假设d -1层的公式为 2（d-1） -1时
深度为d的结点数至少有2(d-1)-1 +2 ,在d-1层的基础上增加2个。所以d层节点数至少为2d -1.
综上，有推论公式得到的结论得此类二叉树的结点数至少为2d-1

二叉树的遍历

(1) 先序遍历

遍历过程：①访问根结点->②先序遍历其左子树->③先序遍历其右子树

void PreOrderTraversal(BinTree BT)
{
    if(BT)
    {
        printf("%d",BT->Data);
        PreOrderTraversal(BT->Left);
        PreOrderTraversal(BT->Right);
    }
}

A(BDFE)(CGIH)

(2)中序遍历

遍历过程：①中序遍历左子树->②访问根结点->③中序遍历其右子树

void InOrderTraversal(BinTree BT)
{
    if(BT)
    {
        PreOrderTraversal(BT->Left);
        printf("%d",BT->Data);
        PreOrderTraversal(BT->Right);
    }
}

(DBEF)A(GHCI)

(3)后序遍历

遍历过程：①后序访问左节点->②后序访问右节点->③访问根节点

void PostOrderTraversal(BinTree BT)
{
    if(BT)
    {
        PreOrderTraversal(BT->Left);
        PreOrderTraversal(BT->Right);
        printf("%d",BT->Data);
    }
}

(DEFB)(HGIC)A

先序、中序、后序遍历过程：遍历过程中经过的路线一样，只是访问各结点的时机不同

二叉树的非递归遍历

(1)中序遍历非递归遍历算法

非递归算法实现的基本思路：使用堆栈

遍历过程：遇到一个结点，就把它入栈，并遍历它的左子树；

当左子树遍历结束后，从栈顶弹出这个结点并访问它；

然后按其右指针再去中序遍历该结点的右子树。

void InOrderTraversal(BinTree BT)
{
    BinTree T = BT;
    Stack S = CreateStack(MaxSize);//创建并初始化堆栈S
    while(T||!IsEmpty(S))
    {
        while(T)
        {
            Push(S,T);//第一次碰到结点，先入栈
            T = T->Left;//再访问左子树
        }
        if(!IsEmpty(S))
        {
            T = Pop(S);//第二次碰到结点，结点弹出堆栈
            pirntf("%5d",T->Data);//(访问)打印结点
            T = T->Right;//转向右子树
        }
    }
    free(S);
}

(2)前序遍历非递归算法

遍历过程：遇到一个结点，就访问(打印)它，并遍历它的左子树；

当左子树遍历结束后，从栈顶弹出这个结点；

然后按其右指针再去前序遍历该结点的右子树。

void PreOrderTraversal(BinTree BT)
{
    BinTree T = BT;
    Stack S = CreateStack(MAXSIZE);
    while(T||!IsEmpty(S))
    {
        while(T)
        {
            Push(S,T);//第一次遇到结点，入栈
            printf("%5d",T->Data);//并访问(打印)
            T = T->Left;//再访问左子树
        }
        if(!IsEmpty(S))
        {
            T = Pop(S);//第二次遇到结点，
            T = T->Right;//访问右子树	
        }
    }
    free(S);
}

(3)后序遍历非递归算法

原先的代码通过更改 print 的位置无法实现后序遍历，因为若发现弹出结点还有右子树时，必须先输出右子树，但此时该节点已经出栈，所以需要再增加条件判断和压栈操作。
法1：

void PostOrderTraversal(BinTree BT) 
{
    BinTree T = BT;
    BinTree temp = NULL; //暂时保存上次输出的树结点
    Stack S = CreateStack(MAXSIZE);
    while (T || !isEmpty(S)) 
    {
        while (T) 
        {
            Push(S, T);
            T = T->Left;
        }
        if (!isEmpty(S)) 
        {
            T = Pop(S);
            // 若右子树为空，或上次抛出的是右儿子，则可以抛出，temp不是NULL就是上次输出的右子树
            if (T->Right == NULL || T->Right == temp) 
            {
                printf("%5d ", T->Data);
                temp = T;    //更新上一次输出的树结点
                T = NULL; // 整个子树遍历完了，指针置为NULL,后续将弹出其父结点
            }
            //若当前结点仍有右子树，则将当前结点重新压入栈，将T指向其右子树
            else 
            {
                push(S, T); 
                T = T->Right;
            }
        }
    }
    //释放栈空间
    free(S);
}

法2：取巧法😂👍(改编自前序遍历，根右左，栈存取Data)

void PostOrderTraversal(BinTree BT)
{
    BinTree T = BT;
    Stack S = CreateStack(MAXSIZE);
    Stack res = CreateStack(MAXSIZE);
    while(T||!IsEmpty(S))
    {
        while(T)
        {
            Push(S,T);//第一次遇到结点，入栈
            Push(res,T->Data);//并访问(打印)
            T = T->Right;//再访问右子树
        }
        if(!IsEmpty(S))
        {
            T = Pop(S);//第二次遇到结点，出栈
            T = T->Left;//访问左子树	
        }
    }
    while(!IsEmpty(res))//弹出数据栈，即倒序输出
    {
        printf("%5d ",res.top());
        res.pop();
    }
    free(S);
    free(res);
}

层序遍历

二叉树遍历的核心问题：二维结构的线形化

从结点访问其左、右儿子结点

访问左儿子后，右儿子结点怎么办？

• 需要一个存储结构保存暂时不访问的结点
• 存储结构：堆栈、队列

队列实现：遍历从根结点开始，首先将根结点入队，接着进入循环(结点出队，访问该结点，其左右儿子入队)

void LevelOrderTraversal(BinTree BT)
{
    Queue Q;
    BinTree T;
    if(!BT) return;
    Q = CreateQueue(MAXSIZE);
    AddQ(Q,BT);
    while(!Isempty(Q))
    {
        T = Delete(Q);
        printf("%d\n",T->Data);
        if(T->Left) AddQ(Q,T->Left);
        if(T->Right) AddQ(Q,T->Right);
    }
}

二叉树的应用问题

例1：求二叉树的高度

法1 dfs 后序遍历

Height = max(Hl,Hr)+1;//某颗树的高度是其左右子树的最大高度加1

因此必须事先求出其左右子树的高度，故使用后序遍历

int PostOrderGetHeight(BinTree BT)
{
	int HL,HR,MaxH;
	if(BT)
    {
		HL = postOrderGetHeight(BT->Left);//求左子树的深度
        HR = postOrderGetHeight(BT->Right);//求右子树的深度
        return (HL>HR?HL:HR)+1;//取左右子树最大深度加1作为该子树的深度
    }
    else return 0;//空树深度为0
}

法2 bfs 层序遍历

每遍历一层，则计数器 +1，直到遍历完成，则可得到树的深度

int maxDepth(TreeNode* root) 
    {
        if(!root) return 0;
        TreeNode* tmp = root;
        queue<TreeNode*>q;
        q.push(root);
        int depth = 0;
        while(!q.empty())
        {
            int size = q.size();
            while(size--)//必须取一层中每个结点，区别于层序遍历
            {
                tmp = q.front();
                q.pop();
                if(tmp->left) q.push(tmp->left);
                if(tmp->right) q.push(tmp->right);
            }
            depth++;//取完一层后深度加一
        }
        return depth;
    }

例2：二元运算表达式及其遍历

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-91WOh07X-1626189219535)(数据结构 第三讲 树 笔记.assets/image-20210618195057820.png)]

前序遍历：++a * bc * + *defg

中序遍历（会受到运算符优先级的影响）：a + b * c + d * e + f * g

解决方案：输出左子树时先输出左括号，结束时再输出右括号

后序遍历：a b c * + d e * f + g * +

例3：由两种遍历序列确定二叉树

两种遍历中其中一个必须为中序

没有中序时，符合序列的二叉树不唯一 (如先序:(AB) 后序:(BA))

先序和中序遍历序列来确定一颗二叉树

【分析】

1. 根据先序遍历序列第一个结点确定根节点

2. 根据根结点在中序遍历序列中分割出左右两个子序列

3. 对左子树和右子树分别递归使用相同的方法继续分解

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-77kxKfyJ-1626189219536)(数据结构 第三讲 树 笔记.assets/image-20210618201049030.png)]

课堂讨论：

1. 对于二叉树，如果其中序遍历结果与前序遍历结果一样，那么可以断定该二叉树所有结点没有左儿子

2. 已知一二叉树的后序和中序遍历的结果分别是FDEBGCA 和FDBEACG,那么该二叉树的前序遍历结果是什么？ABDFECG

   ---

   题目练习

   树的同构：给定两棵树T1，T2。如果T1可以通过若干次左右孩子互换就变成T2，则称两棵树是”同构“的。

   现给定两棵树，判断它们是否是同构的？

   输入格式: 输入给出2棵二 叉树的信息：先在一行中给出该树的结点数，随后N行。第 i 行对应编号第 i 个结点，给出该结点中存储的字母、其左孩子结点的编号、右孩子结点的编号。 如果孩子结点为空，则在相应位置上给出“-”。

   求解思路：

   1. 二叉树表示

      结构数组表示二叉树：静态链表

      #define MaxTree 10
      #define ElementType char
      #define Tree int
      #define Null -1
      struct TreeNode
      {
          ElementType Element;
          Tree Left;
          Tree Right;
      }T1[MaxTree],T2[MaxTree];
      

      [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5PFsHiO0-1626189219536)(数据结构 第三讲 树 笔记.assets/image-20210618211239521.png)]

      找根结点：在数组中发现1号结点不做任何结点的左右儿子，故1号结点A为根结点

   2. 建二叉树

      Tree BuildTree( struct TreeNode T[] )
      {
      scanf("%d\n", &N);
      if (N) {
      for (i=0; i<N; i++) check[i] = 0;
      for (i=0; i<N; i++) {
      scanf("%c %c %c\n", &T[i].Element, &cl, &cr);
      if (cl != '-') {
      T[i].Left = cl-'0';
      check[T[i].Left] = 1;
      }
      else T[i].Left = Null;
      if (cr != '-') {
      T[i].Right = cr-'0';
      check[T[i].Right] = 1;
      }
      else T[i].Right = Null;
      }
      for (i=0; i<N; i++)
       if (!check[i]) break;
      Root = i;
      }
      return Root;
      

   3. 同构判别

int Isomorphic( int r1, int r2 )
{
	if( r1 == -1 && r2 == -1 )      //如果两颗树均为空，认为他们同构 
		return 1;
	if( ( r1 == -1 && r2 != -1 ) || ( r1 != -1 && r2 == -1 ) )    //如果两棵树只有一颗为空，认为他们不同构
		return 0;
	if( T1[ r1 ].data != T2[ r2 ].data )           //如果两棵树根结点的值都不同，则不同构 
		return 0; 
	if( T1[ r1 ].Left == -1 && T2[ r2 ].Left == -1 )   //l两棵树左边子树都为空就去递归的找他们的右子树
		return Isomorphic( T1[ r1 ].Right, T2[ r2 ].Right );
	if( ( T1[ r1 ].Left != -1 && T2[ r2 ].Left != -1 ) && ( T1[ T1[r1].Left ].data == T2[ T2[r2].Left ].data ) ){  //如果左子树相同且左子树数据也相同 
		return Isomorphic( T1[ r1 ].Left, T2[ r2 ].Left ) && Isomorphic( T1[ r1 ].Right, T2[ r2 ].Right );//然后递归的进入左右子树去判断是否同构 
	} 
	else{  //如果两个左子树有为空的或者两个左子树数据不相同，就交换左右子树递归的去判断 
		return Isomorphic( T1[ r1 ].Left, T2[ r2 ].Right ) && Isomorphic( T1[ r1 ].Right, T2[ r2 ].Left );
	}
}

二叉搜索树（二叉排序树/二叉查找树）

定义：一颗二叉树，可以为空；若不为空，满足以下性质：

1. 非空左子树的所有键值小于其根节点的键值。
2. 非空右子树的所有键值大于其根结点的键值。
3. 左、右子树都是二叉搜索树。

二叉树的查找操作：Find

查找从根结点开始，若树为空，返回NULL

若搜索树非空，则根结点关键字和X进行比较，并进行不同处理：

1. 若X小于根结点键值，只需在左子树中搜索
2. 若X大于根结点键值，只需在右子树中搜索
3. 若两者比较结果是相等，搜索完成，返回指向此节点的指针

Position Find(ElementType X,BinTree BST)//递归法
{
    if(!BST) return NULL;//查找失败
    if(X > BST->Data) Find(X,BST->Right);//在右子树中查找
    else if(X < BST->Data) Find(X,BST->Left);//在左子树中查找
    else return BST;//查找成功，返回找到结点的地址
}
/*由于非递归函数的执行效率更高，可将“尾递归”函数改为迭代函数*/
Position Find(ElementType X,BinTree BST)//循环法
{
    while(BST)
    {
        if(X > BST->Data) BST = BST->Right;
        else if(X == BST->Data) return BST;
        else BST = BST->Left;
    }
    return NULL;//查找失败
}

查找最大、最小元素的递归函数

Position FindMin(BinTree BST)
{
    if(!BST) return NULL;
    else if(!BST->Left) return BST;//找到最左叶结点并返回
    else return FindMin(BST->Left);//沿左分支继续查找
}
Position FindMax(BinTree BST)
{
    if(!BST) return NULL;
    else if(!BST->Right) return BST;//找到最右叶结点并返回
    else return FindMax(BST->Right);//沿右分支继续查找
}

二叉搜索树的插入

关键是要找到元素应该插入的位置，可以采用与Find类似的方法

BinTree Insert(ElementType X,BinTree BST)
{
    if(!BST)//若原树为空，生成并返回一个结点的二叉搜索树
    {
		BST = (BinTree)malloc(sizeof(TreeNode));
        BST->Data = X;
        BST->Left = BST->Right = NULL;
    }
    else if(X > BST->Data)
        BST->Right = Insert(X,BST->Right);//递归插入右子树，理解时用插入叶结点的情况去想
    else if(X < BST->Data)
        BST->Left = Insert(X,BST->Left);//递归插入左子树，理解时用插入叶结点的情况去想
    //else X结点存在，什么都不做
    return BST;//最后返回结点
}

二叉搜索树的删除

考虑三种情况：

1. 要删除的是叶结点：直接删除，并修改其父节点指针——置为NULL

2. 要删除的是只有一个孩子的结点：将其父节点的指针指向要删除的结点的孩子结点

3. 要删除的结点有左、右两棵子树：用另一节点替代被删除结点：右子树的最小元素 或者 左子树的最大元素

   理由：左子树的最大值和右子树的最小值一定不是有两个儿子的结点

BinTree Delete(ElementType X,BinTree BST)
{
    Position Tmp;
    if(!BST) printf("要删除的元素未找到！");
    else if(X < BST->Data) BST->Left = Delete(X,BST->Left);//左子树递归删除
    else if(X > BST->Data) BST->Right = Delete(X,BST->Right);//右子树递归删除
    else//找到要删除的结点
    {
        if(BST->Left && BST->Right)//被删除的结点有左右两个儿子
        {
            Tmp = FindMin(BST->Right);//在右子树中找到最小值结点
            BST->Data = Tmp->Data;//赋值
            BST->Right = Delete(BST->Data,BST->Right);//赋值后删除
        }
        else//被删除的结点有一个儿子或者没有儿子
        {
            Tmp = BST;
            if(BST->Left==NULL) BST = BST->Right;//如果右儿子存在或者没有儿子
            else if(BST->Right==NULL) BST = BST->Left;//如果左儿子存在或者没有儿子
            free(Tmp);
        }
    }
    return BST;
}
BinTree FindMin(BinTree BST)
{
    if(!BST) return NULL;
    while(BST->Left) BST = BST->Left;
    return BST;
}

若一搜索树（查找树）是一个有n个结点的完全二叉树，则该树的最大值一定在叶结点上 (×)

若一搜索树（查找树）是一个有n个结点的完全二叉树，则该树的最小值一定在叶结点上 (√)

注意理解完全二叉树的概念

平衡二叉搜索树

搜索树结点不同插入次序，将导致不同的深度和平均查找长度ASL

平衡因子(Balance Factor，简称BF)：BF(T) = hL-hR,其中hL和hR分别为T的左、右子树的高度

平衡二叉树(Balance Binary Tree，简称AVL树)：空树，或者任一节点左、右子树的高度差的绝对值不超过1，即**|BF(T)| <= 1**

平衡二叉树的高度能达到log2 n吗？

设nh是高度为h的平衡二叉树的最少结点数。结点数最少时：nh = n(h-1) + n(h-2) + 1

给定结点数为n的AVL树的最大高度为O(log2 n)

层数 = 高度 + 1

平衡二叉树的调整

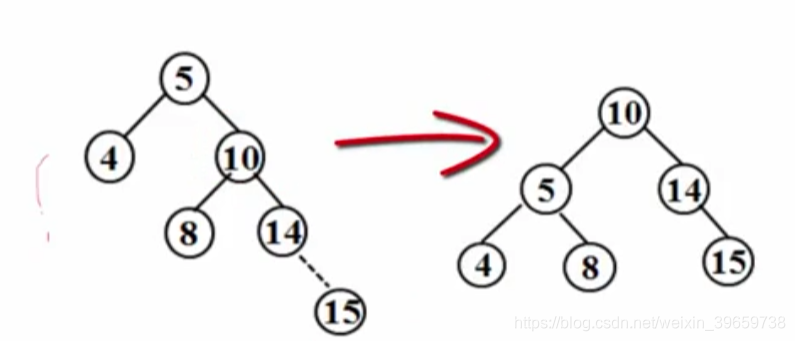
RR旋转（右单旋）

平衡二叉树的相关代码

typedef struct AVLNode *Position;
typedef Position AVLTree; /* AVL树类型 */
struct AVLNode{
    ElementType Data; /* 结点数据 */
    AVLTree Left;     /* 指向左子树 */
    AVLTree Right;    /* 指向右子树 */
    int Height;       /* 树高 */
};

int Max ( int a, int b )
{
    return a > b ? a : b;
}

AVLTree SingleLeftRotation ( AVLTree A )
{ /* 注意：A必须有一个左子结点B */
  /* 将A与B做左单旋，更新A与B的高度，返回新的根结点B */     

    AVLTree B = A->Left;
    A->Left = B->Right;
    B->Right = A;
    A->Height = Max( GetHeight(A->Left), GetHeight(A->Right) ) + 1;
    B->Height = Max( GetHeight(B->Left), A->Height ) + 1;
 
    return B;
}
AVLTree SingleRightRotation(AVLTree A) {
	AVLTree B = A->Right;
	A->Right = B->Left;
	B->Left = A;
	A->Height = Max(GetHeight(A->Left), GetHeight(A->Right)) + 1;
	B->Height = Max(GetHeight(B->Right), A->Height) + 1;
	return B;
}

AVLTree DoubleLeftRightRotation ( AVLTree A )
{ /* 注意：A必须有一个左子结点B，且B必须有一个右子结点C */
  /* 将A、B与C做两次单旋，返回新的根结点C */
    
    /* 将B与C做右单旋，C被返回 */
    A->Left = SingleRightRotation(A->Left);
    /* 将A与C做左单旋，C被返回 */
    return SingleLeftRotation(A);
}
AVLTree DoubleRightLeftRotation(AVLTree A) {
	A->Right = SingleLeftRotation(A->Right);
	return SingleRightRotation(A);
}


AVLTree Insert( AVLTree T, ElementType X )
{ /* 将X插入AVL树T中，并且返回调整后的AVL树 */
    if ( !T ) { /* 若插入空树，则新建包含一个结点的树 */
        T = (AVLTree)malloc(sizeof(struct AVLNode));
        T->Data = X;
        T->Height = 0;
        T->Left = T->Right = NULL;
    } /* if (插入空树) 结束 */

    else if ( X < T->Data ) {
        /* 插入T的左子树 */
        T->Left = Insert( T->Left, X);
        /* 如果需要左旋 */
        if ( GetHeight(T->Left)-GetHeight(T->Right) == 2 )
            if ( X < T->Left->Data ) 
               T = SingleLeftRotation(T);      /* 左单旋 */
            else 
               T = DoubleLeftRightRotation(T); /* 左-右双旋 */
    } /* else if (插入左子树) 结束 */
    
    else if ( X > T->Data ) {
        /* 插入T的右子树 */
        T->Right = Insert( T->Right, X );
        /* 如果需要右旋 */
        if ( GetHeight(T->Left)-GetHeight(T->Right) == -2 )
            if ( X > T->Right->Data ) 
               T = SingleRightRotation(T);     /* 右单旋 */
            else 
               T = DoubleRightLeftRotation(T); /* 右-左双旋 */
    } /* else if (插入右子树) 结束 */

    /* else X == T->Data，无须插入 */

    /* 别忘了更新树高 */
    T->Height = Max( GetHeight(T->Left), GetHeight(T->Right) ) + 1;
    
    return T;
}

LL旋转（左单旋）

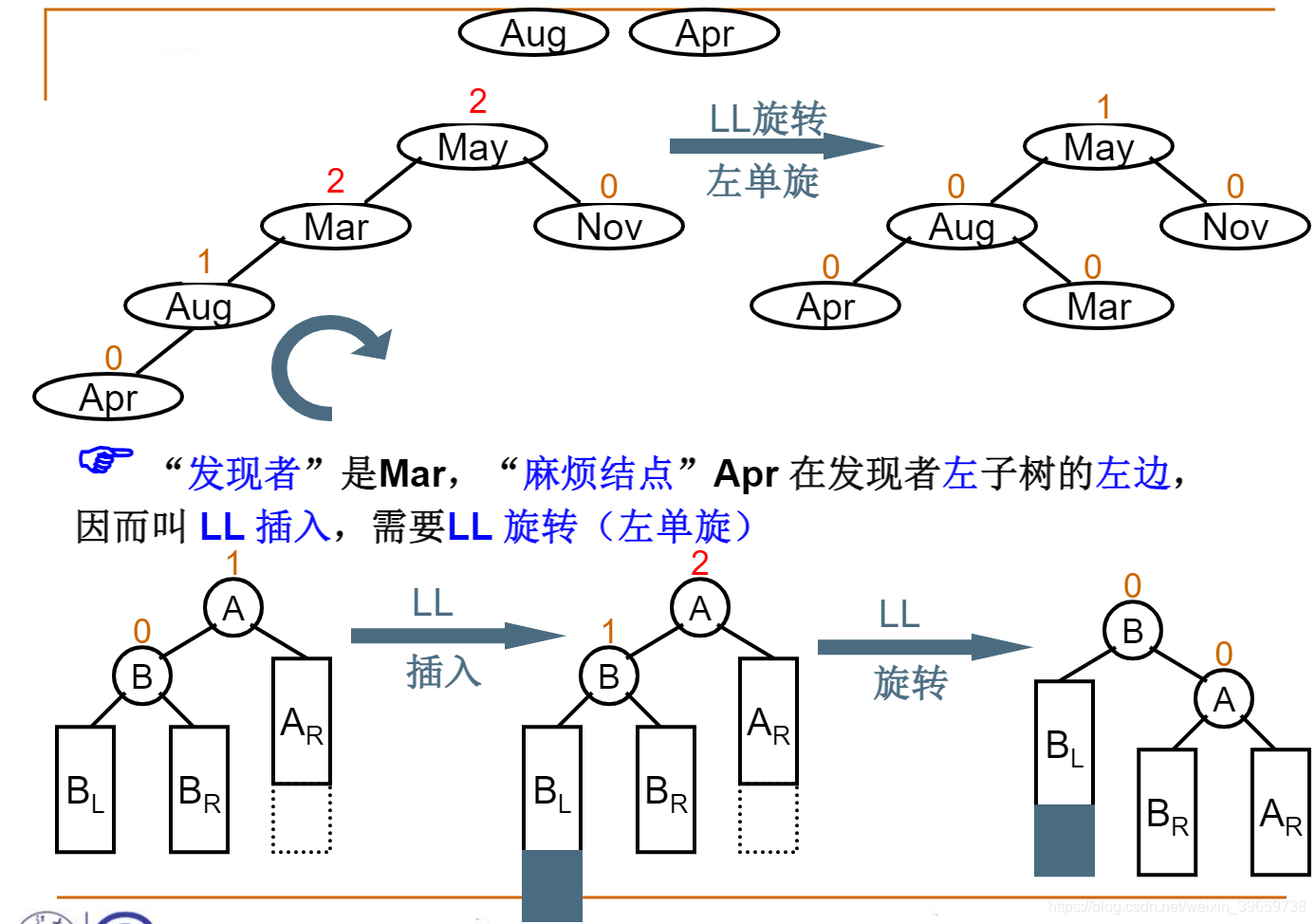
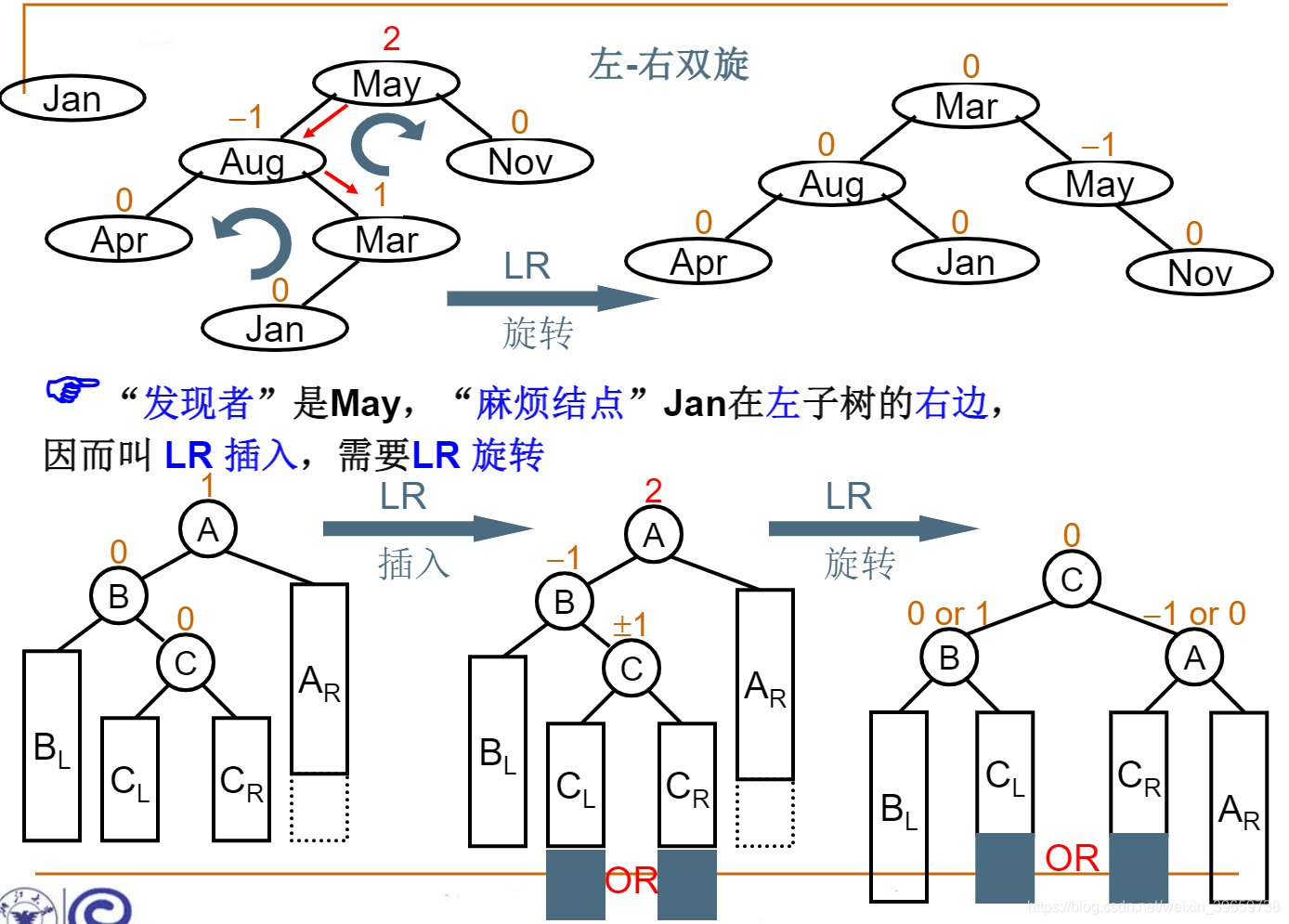
LR旋转（左右双旋）

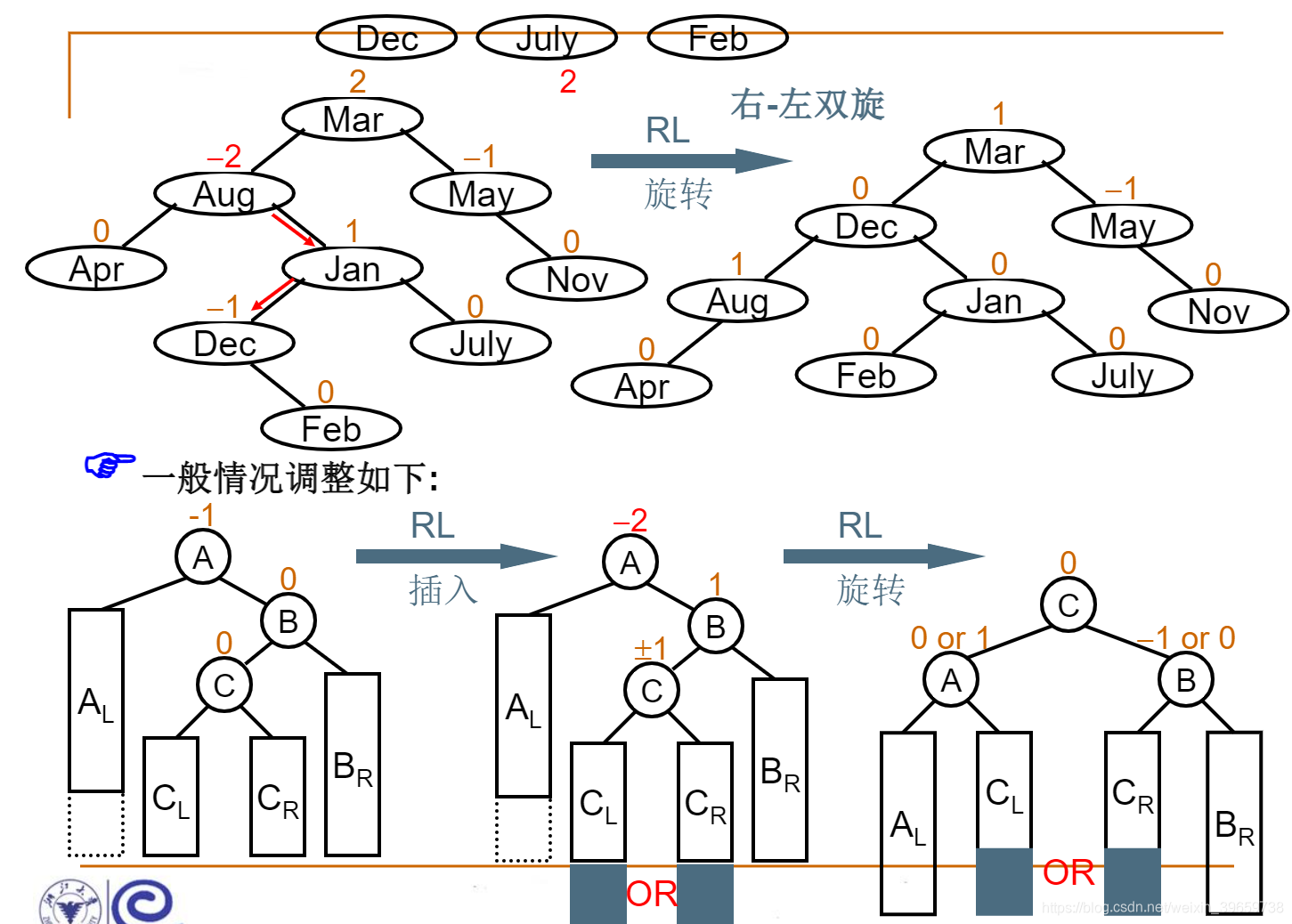
RL旋转（右左双旋）

小白专场：是否属于同一棵二叉搜索树

给定一个插入序列就可以唯一确定一棵二叉搜索树。然而，一棵给定的二叉搜索树却可以由多种不同的插入序列得到。例如分别按照序列{2, 1, 3}和{2, 3, 1}插入初始为空的二叉搜索树，都得到一样的结果。于是对于输入的各种插入序列，你需要判断它们是否能生成一样的二叉搜索树。

输入格式:

输入包含若干组测试数据。每组数据的第1行给出两个正整数N (≤10)和L，分别是每个序列插入元素的个数和需要检查的序列个数。第2行给出N个以空格分隔的正整数，作为初始插入序列。最后L行，每行给出N个插入的元素，属于L个需要检查的序列。

简单起见，我们保证每个插入序列都是1到N的一个排列。当读到N为0时，标志输入结束，这组数据不要处理。

输出格式:

对每一组需要检查的序列，如果其生成的二叉搜索树跟对应的初始序列生成的一样，输出“Yes”，否则输出“No”。

输入样例:

4 2
3 1 4 2
3 4 1 2
3 2 4 1
2 1
2 1
1 2
0

输出样例:

Yes
No
No

求解思路

两个序列是否对应相同搜索树的判别：

1. 分别建两棵搜索树的判别方法：根据两个序列分别建树，在判别树是否一样

2. 不建树的判别方法：先找到根结点数，再按顺序找出左右子树，观察左右子树是否相同

3. 建一棵树，再判别其他序列是否与该树一致

   3.1 搜索树表示

   typedef struct TreeNode *Tree;
   struct TreeNode
   {
       int v;
       Tree Left,Right;
       int flag;//判别一个序列是否跟树一致，没访问过为0，访问过为1
   };
   

   3.2 建搜索树T

   Tree MakeTree(int N)
   {
       Tree T;
       int i,V;
       scanf("%d",&V);
       T = NewNode(V);
       for(int i=1;i<N;i++)
       {
           scanf("%d",&V);
           T = Insert(T,V);
       }
       return T;
   }
   Tree NewNode(int V)
   {
       Tree T = (Tree)malloc(sizeof(struct TreeNode));
       T->v = V;
       T->Left = T->Right = NULL;
       T->flag = 0;
       return T;
   }
   Tree Insert(Tree T,int V)
   {
       if(!T) T = NewNode(V);
       else
       {
           if(V > T->V)
           {
               T->Right = Insert(T->Right,V);
           }
           else if(V < T->V)
           {
               T->Left = Insert(T->Left,V);
           }
       }
       return T;
   }
   

   3.3 判别一序列是否与搜索树T一致

   方法：在树T中按顺序搜索序列中的每一个数，如果每次搜索所经过的结点在前面均出现过，则一致。否则(某次搜索中遇到前面未出现过的结点)，则不一致

   int check(Tree T,int V)
   {
       if(T->flag)
       {
           if(V < T->V) return check(T->Left,V);
           else if(V > T->V) return check(T->Right,V);
           else return 0;//说明序列中存在两个相同的数。不合逻辑，认为不一致
       }
       else
       {
           if(T->V==V)
           {
               T->flag = 1;
               return 1;
           }
           else return 0;//没找到, 认为不一致
       }
   }
   int Judge(Tree T,int N)
   {
       int i,V,flag=1;//flag为0代表不一致，为1代表一致，这样处理可以保证序列被全部读入程序，避免检查下一个序列时出现bug
       scanf("%d",&V);
       if(V!=T->V) flag=0;
       else T->flag=1;//已经搜索过
       for(i=1;i<N;i++)
       {
           scanf("%d",&V);
           if((flag)&&(!check(T,V))) flag=0;//当不一致时直接continue，不进入check函数
       }
       if(!flag) return 0;
       else return 1;
   }
   void ResetT(Tree T)
   {
       T->flag = 0;
       if(T->Left) ResetT(T->Left);
       if(T->Right) ResetT(T->Right);
   }
   void FreeTree(Tree T)
   {
       if(T->Left) FreeTree(T->Left);
       if(T->Right) FreeTree(T->Right);
       Free(T);//顺序不可更换
   }
   

int main()
{
	int N,L,i;
    Tree T;
    
    scanf("%d",&N);
    while(N)
    {
        scanf("%d",&L);
        T = MakeTree(N);
        for(i=0;i<L;i++)
        {
            if(Judge(T,N)) printf("Yes\n");
            else printf("No\n");
            ResetT(T);//清除T中的标记flag
        }
        FreeTree(T);//释放树，为下一次建树做准备
        scanf("%d",&N);
    }
    return 0;
}