参考:
原作者总结出来的解决算法的一个技巧:把大的问题细化到一个点,先研究在这个小的点上如何解决问题,然后再通过递归/迭代的方式扩展到整个问题。
本文从「最长公共子序列问题」展开,总结三道子序列问题,解这道题仔细讲讲这种子序列问题的套路,你就能感受到这种思维方式了。
1 最长公共子序列
计算1143. 最长公共子序列(Longest Common Subsequence,简称 LCS)是一道经典的动态规划题目:

力扣第 1143 题就是这道题,函数签名如下:
int longestCommonSubsequence(String s1, String s2);
首先,我们先考虑暴力算法:把s1和s2的所有子序列都穷举出来,然后看看有没有公共的,然后在所有公共子序列里面再寻找一个长度最大的。
然后,我们在暴力算法的基础上进行改进:我们可以不要考虑整个字符串,而是细化到s1和s2的每个字符。
在“子序列解题模板”中有一个规律:
对于两个字符串求子序列的问题,都是用两个指针
i和j分别在两个字符串上移动,大概率是动态规划思路。
思路:具体到每一个字符,思考每个字符该做什么
接下来,咱不要看s1和s2两个字符串,而是要具体到每一个字符,思考每个字符该做什么。
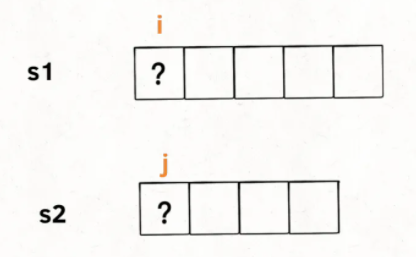
我们只看s1[i]和s2[j],
-
如果
s1[i] == s2[j],说明这个字符一定在lcs中:
-
如果
s1[i] != s2[j],应该怎么办呢?s1[i] != s2[j]意味着,s1[i]和s2[j]中至少有一个字符不在lcs中:
如上图,总共可能有三种情况,我怎么知道具体是那种情况呢?
答:其实我们也不知道,那就把这三种情况的答案都算出来,取其中结果最大的那个呗,因为题目让我们算「最长」公共子序列的长度嘛。
这里我们可以进行一个优化,我们可以观察情况3:
情况三在计算
s1[i+1..]和s2[j+1..]的lcs长度,这个长度肯定是小于等于情况二s1[i..]和s2[j+1..]中的lcs长度的,因为s1[i+1..]比s1[i..]短嘛,那从这里面算出的lcs当然也不可能更长嘛。同理,情况三的结果肯定也小于等于情况一。
也就是说,情况三被情况一和情况二包含了,所以我们可以直接忽略掉情况三。
现在我们大致思路已经有了,就是:注意对比每一个字符,它们有两种可能:
s1[i] == s2[j]时,LCS加1;s1[i] != s2[j]时,分三种情况讨论。(实际上,情况3包含在情况1和2之中。)
代码实现
1、不使用「dp数组」,也不使用「备忘录」的动态规划:
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
if (text1.size() == 0 || text2.size() == 0) return 0;
return dp(text1, 0, text2, 0);
}
int dp(string text1, int i, string text2, int j) {
// base case
if (i == text1.size() || j == text2.size())
return 0;
// 状态转移
if (text1[i] == text2[j])
return dp(text1, i + 1, text2, j + 1) + 1;
// else if (text1[i] != text2[j])
return max(
dp(text1, i, text2, j + 1),
max(dp(text1, i + 1, text2, j),
dp(text1, i + 1, text2, j + 1)) // 这里可以优化
);
}
};
说明:
-
我们的
dp函数含义为:// 定义:计算 s1[i..] 和 s2[j..] 的最长公共子序列长度 int dp(String s1, int i, String s2, int j) -
情况3我们其实可以不写,但这里为了代码的直观性,还是加上了。
2、使用「dp数组」(迭代实现):
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
int m = text1.size();
int n = text2.size();
// dp数组:dp[i][j]表示s1[i..] 和 s2[j..] 的最长公共子序列长度
vector<vector<int>> dp(m+1, vector<int>(n+1, -1));
// 初始情况
for (int j = 0; j < n; j++) {
dp[0][j] = 0;
}
for (int i = 0; i < m; i++) {
dp[i][0] = 0;
}
// 状态转移
// 注意i、j的值,因为我们多给dp数组增加了一行、一列,此时text的下标需要注意
for (int i = 1; i <= m; i++) {
int ii = i - 1;
for (int j = 1; j <= n; j++) {
int jj = j - 1;
if (text1[ii] == text2[jj]) // 相等时
dp[i][j] = dp[i - 1][j - 1] + 1;
else if (text1[ii] != text2[jj]) { // 不相等时,分三种情况讨论
int a = dp[i-1][j]; // 情况1:text1[i] 不在 lcs 中
int b = dp[i][j - 1]; // 情况2:text2[j] 不在 lcs 中
int c = dp[i-1][j - 1]; // 情况3:text1[i]、text2[j] 均不在 lcs 中
dp[i][j] = max(a, max(b, c)); // 找出这三种情况最大的
}
}
}
return dp[m][n];
}
};
说明:
-
注意我们这里的
text[]和dp[][]的下标。
可以看到,我们声明的dp数组是
dp[m+1][n+1]大小的,这是因为,我们需要考虑空字符串的情况,所以需要多一行、多一列来存储。而
text1[]的下表范围在0~ m-1和text2[]的下表范围在0~ n-1。所以,在带入下标值时,需要区分dp和text的下标。
3、使用「备忘录」(递归实现):
//添加备忘录
class Solution {
public:
// memo 备忘录:text1[i,...] 、text2[j,...]的最长公共子序列
vector<vector<int>> memo;
int longestCommonSubsequence(string text1, string text2) {
for (int i = 0; i < text1.size(); i++) {
memo.push_back(vector<int>(text2.size(), -1));
}
if (text1.size() == 0 || text2.size() == 0) return 0;
return dp(text1, 0, text2, 0);
}
int dp(string text1, int i, string text2, int j) {
// base case
if (i == text1.size() || j == text2.size())
return 0;
// 状态转移
if (memo[i][j] != -1)// 如果之前计算过,则直接返回备忘录中的答案
return memo[i][j];
if (text1[i] == text2[j])
memo[i][j] = dp(text1, i + 1, text2, j + 1) + 1;
// return dp(text1, i + 1, text2, j + 1) + 1;
else if (text1[i] != text2[j]) {
memo[i][j] = max(
dp(text1, i, text2, j + 1),
max(dp(text1, i + 1, text2, j),
dp(text1, i + 1, text2, j + 1))
);
}
return memo[i][j];
}
};
进阶:空间优化
这里我们可以来练习空间优化,详细的可见前文的 状态压缩 一文。
首先,看上一小节中的使用「dp数组」实现的代码。发现在求dp[i][j]时需要[i-1][j]、[i][j-1]、[i-1][j-1]位置的值。
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
int m = text1.size();
int n = text2.size();
// dp数组:dp[i][j]表示s1[i..] 和 s2[j..] 的最长公共子序列长度
//vector<vector<int>> dp(m + 1, vector<int>(n + 1, -1));
vector<int> dp(n + 1, -1);
// 初始情况:相当于dp[0][j]
for (int j = 0; j <= n; j++) {
dp[j] = 0;
}
// 状态转移
// 注意i、j的值,因为我们多给dp数组增加了一行、一列,此时text的下标需要注意
for (int i = 1; i <= m; i++) {
int ii = i - 1;
int temp = dp[0];
dp[0] = 0; // 更新,相当于每一行的第0列
for (int j = 1; j <= n; j++) {
int pre = temp; // pre 实际上对应dp[i-1][j-1]
temp = dp[j];
int jj = j - 1;
if (text1[ii] == text2[jj]) // 相等时
//dp[i][j] = dp[i - 1][j - 1] + 1;
dp[j] = pre;
else if (text1[ii] != text2[jj]) { // 不相等时,分三种情况讨论
//int a = dp[i - 1][j]; // 情况1:text1[i] 不在 lcs 中
int a = dp[j];
//int b = dp[i][j - 1]; // 情况2:text2[j] 不在 lcs 中
int b = dp[j - 1];
//int c = dp[i - 1][j - 1]; // 情况3:text1[i]、text2[j] 均不在 lcs 中
int c = pre;
dp[i][j] = max(a, max(b, c)); // 找出这三种情况最大的
}
}
}
return dp[n];
}
};
2 字符串删除操作
力扣第 583 题「两个字符串的删除操作」,看下题目:
函数签名如下:
int minDistance(String s1, String s2);
题目让我们计算将两个字符串变得相同的最少删除次数,那我们可以思考一下,最后这两个字符串会被删成什么样子?
答:删除的结果就是它俩的最长公共子序列嘛!
所以,我们这一题可以直接套用上一题的代码,只需要加一点点即可:
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
int m = text1.size();
int n = text2.size();
// dp数组:dp[i][j]表示s1[i..] 和 s2[j..] 的最长公共子序列长度
vector<vector<int>> dp(m+1, vector<int>(n+1, -1));
// 初始情况
for (int j = 0; j < n; j++) {
dp[0][j] = 0;
}
for (int i = 0; i < m; i++) {
dp[i][0] = 0;
}
// 状态转移
// 注意i、j的值,因为我们多给dp数组增加了一行、一列,此时text的下标需要注意
for (int i = 1; i <= m; i++) {
int ii = i - 1;
for (int j = 1; j <= n; j++) {
int jj = j - 1;
if (text1[ii] == text2[jj]) // 相等时
dp[i][j] = dp[i - 1][j - 1] + 1;
else if (text1[ii] != text2[jj]) { // 不相等时,分三种情况讨论
int a = dp[i-1][j]; // 情况1:text1[i] 不在 lcs 中
int b = dp[i][j - 1]; // 情况2:text2[j] 不在 lcs 中
int c = dp[i-1][j - 1]; // 情况3:text1[i]、text2[j] 均不在 lcs 中
dp[i][j] = max(a, max(b, c)); // 找出这三种情况最大的
}
}
}
// return dp[m][n];
int LCS = dp[m][n];
return m - LCS + n - LCS;
}
};
3 最小 ASCII 删除和
LeetCode的712. 两个字符串的最小ASCII删除和:

这道题,和上一道题非常类似,这回不问我们删除的字符个数了,问我们删除的字符的 ASCII 码加起来是多少。
那就不能直接复用计算最长公共子序列的函数了,但是可以依照之前的思路,稍微修改 base case 和状态转移部分即可直接写出解法代码:
- 我们的dp数组含义需要修改为:将 s1[i…] 和 s2[j…] 删除成相同字符串,最小的 ASCII 码之和为 dp(s1, i, s2, j)。
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
int res = 0; // 存储ASCII的值
int m = text1.size();
int n = text2.size();
// dp数组:dp[i][j]表示s1[i..] 和 s2[j..] 的最长公共子序列长度
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
// 初始情况
for (int j = 1; j <= n; j++) {
dp[0][j] = text2[j-1] + dp[0][j - 1];
}
for (int i = 1; i <= m; i++) {
dp[i][0] = text1[i-1] + dp[i - 1][0];
}
// 状态转移
// 注意i、j的值,因为我们多给dp数组增加了一行、一列,此时text的下标需要注意
for (int i = 1; i <= m; i++) {
int ii = i - 1;
for (int j = 1; j <= n; j++) {
int jj = j - 1;
if (text1[ii] == text2[jj]) // 相等时
dp[i][j] = dp[i - 1][j - 1];
else if (text1[ii] != text2[jj]) { // 不相等时,分三种情况讨论
int a = dp[i - 1][j] + text1[ii]; // 情况1:text1[i] 不在 lcs 中
int b = dp[i][j - 1] + text2[jj]; // 情况2:text2[j] 不在 lcs 中
int c = dp[i - 1][j - 1] + text1[ii] + text2[jj]; // 情况3:text1[i]、text2[j] 均不在 lcs 中
dp[i][j] = min(a, min(b, c)); // 找出这三种情况最大的
}
}
}
return dp[m][n];
}
};
4 小结
至此,三道子序列问题就解决完了,关键在于将问题细化到字符,根据每两个字符是否相同来判断他们是否在结果子序列中,从而避免了对所有子序列进行穷举。