[数据结构与算法]数据结构 第四次 实验报告

数据结构 第四次 实验报告

西北工业大学数据结构实验作业

Author’s email: xiangyushun@mail.nwpu.edu.cn Date: 2021/6/2

实验 4.1

• 实验题目：实验 4.1：求赋权图中一个结点到所有结点的最短路径的长度
• 实验目的：了解无向图的最短路径算法——Dijkstra算法
• 实验内容：用迪杰斯特拉算法求一点到其余所有结点的最短路径

一、需求分析

1. 输入的形式

先输入一个小于 100 的正整数 n，然后输入图的邻接矩阵（10000 表示无穷大，即两点之间没有边）

2. 输出的形式

先用迪杰斯特拉算法求给定的第一个点到其余所有结点的最短路径。然后再输出给定的两个点之间的最短路径（按顺序输出最短路径上的每一个点，每个数据占一行）

3. 程序所要达到的功能

用Dijkstra算法求一点到其余所有结点的最短路径

4. 测试数据

样例输入：

6 
0 1 4 10000 10000 10000
1 0 2 7 5 10000
4 2 0 10000 1 10000
10000 7 10000 0 3 2
10000 5 1 3 0 6
10000 10000 10000 2 6 0

样例输出：

0 
1 
3 
7 
4 
9 

二、概要设计

1. 用邻接矩阵记录一个无向图（是一个对称矩阵）
2. 对该无向图利用Dijkstra算法求出原点到其他点的最短路径
3. 依次输出原点到其他点的最短路径

基本操作

以邻接矩阵为存储结构的无向图

用于储存具体数据（点的个数、点与点之间的距离）

class AdjMatrixGraph
{
public:
	AdjMatrixGraph(int n); // 构造函数
	~AdjMatrixGraph(); // 析构函数
	void Dijkstra(int firstPoint, int* distanceList) const; // Dijkstra算法
private:
	int** m_adjMatrix; // 邻阶矩阵
	int m_vexNum; // 点的个数
};

distanceList数组

用于储存源点到各个点的距离

析构函数——初始化邻接矩阵

AdjMatrixGraph::AdjMatrixGraph(int n)

析构函数——销毁邻接矩阵

AdjMatrixGraph::~AdjMatrixGraph()

Dijkstra算法——最短路径算法

void AdjMatrixGraph::Dijkstra(int firstPoint, int* distanceList)

程序调用图

解释：

• 粗线表示程序总的流程
• 细线表示一些函数与变量或对象的调用关系
• 方括号表示变量或对象
• 棱形表示函数
• 圆表示一个变量（结构体，数组）

三、详细设计

我们以样例为例，探究如何完成这道实验题

样例输入：

6 
0 1 4 10000 10000 10000
1 0 2 7 5 10000
4 2 0 10000 1 10000
10000 7 10000 0 3 2
10000 5 1 3 0 6
10000 10000 10000 2 6 0

样例输出：

0
1
3
7
4
9

分析样例

画出无向图

依题意，求顶点v0到其他各点的最短路径

首先第一步，我们先声明一个distance数组，该数组初始化的值为

0 1 4 INF INF INF

这里INF的大小为10000，表示两个点之间不连通

我们的顶点集book的初始化为：book = {v0} （若点对应book数组中的值为true时，代表在点集内）

既然是求 v0 顶点到其余各个顶点的最短路程，那就先找一个离 0 号顶点最近的顶点。通过数组 distance 可知当前离v0 顶点最近是 v1 顶点。当选择了 1 号顶点后，distance[1]（下标从0开始）的值就已经从“估计值”变为了“确定值”，即 v0 顶点到 v1 顶点的最短路程就是当前 dis[1]值。将v1加入到 book 中。
为什么呢？因为目前离 v0 顶点最近的是 v1顶点，并且这个图所有的边都是正数，那么肯定不可能通过第三个顶点中转，使得 v0 顶点到 v1 顶点的路程进一步缩短了。因为 v0 顶点到其它顶点的路程肯定没有 v0 到 v1 顶点短.

OK，既然确定了一个顶点的最短路径，所以更新distance[1]的值,得到如下结果：

0 1 3 8 6 INF

继续重复上述步骤即可

最后我们会得到

0 1 3 7 4 9

即我们应输出的数组

邻接矩阵的构造函数

这里的先初始化类成员变量m_vexNum

再为二维指针申请内存空间

最后读入数据到m_adjMatrix，完成类的初始化

djMatrixGraph::AdjMatrixGraph(int n) :m_vexNum(n)
{
	this->m_adjMatrix = new int* [n];
	for (int i = 0; i < n; i++) {
		this->m_adjMatrix[i] = new int[n];
	}
	std::cout << "Please enter the adjacent matrix of the graph" << std::endl;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			std::cin >> this->m_adjMatrix[i][j];
		}
	}
}

时间复杂度：$O(n^2)$

邻接矩阵的析构函数

对于一个由二维指针申请的堆空间的释放

AdjMatrixGraph::~AdjMatrixGraph()
{
	// 二维指针的析构
	for (int i = 0; i < this->m_vexNum; i++) {
		delete[] this->m_adjMatrix[i];
		this->m_adjMatrix[i] = nullptr;
	}
	delete[] this->m_adjMatrix;
	this->m_adjMatrix = nullptr;
}

时间复杂度：$O(n^2)$

Dijkstra算法

注：EDGEDISTANCE_MAN表示两个点之间没有边（其值为10000）

Dijkstra（迪杰斯特拉）提出了一个按路径长度递增的次序产生最短路径的算法（贪心算法）：

? 首先，引入辅助向量D，它的每个分量D[i]表示当前所找到的从始点v0到每个找到vi的最短路径的长度。它的初始状态为：若从v0到vi有弧，则D[i]为弧上的权值；否则为无穷大。显然长度为

D[j] = Min { D[i] | $v_i\in V$}

的路径就是从v出发的长度最短的一条路径，此路径为(v,vj)。

? 那么下一条长度次短的最短路径是哪一条呢？假设该次短路径的终点是vk, 则这条路径或者是(v, vk)，或者是(v, vj, vk)。 一般情况下，假设S为已求得最短路径的终点的集合，可以使用该算法。

void AdjMatrixGraph::Dijkstra(int firstPoint, int* distance) const
{
	int tempPoint; // 临时的点，记录上一个遍历的点
	int min, i, j;
	bool* book = new bool[this->m_vexNum]; // 一个点集，用于存放已经确定最短路径的点
	
	// 初始化各数组
	for (int i = 0; i < this->m_vexNum; i++) {
		book[i] = false; // 这时还未遍历任何一个点
		distance[i] = EDGEDISTANCE_MAN;
	}

	/*  已遍历源点，且源点到源点的距离为0 */
	book[firstPoint] = true; // 将起点加入集合
	distance[firstPoint] = 0; // 起点到自己的距离为0 //

	// 对从原点出发的边进行统计
	for (i = 0; i < this->m_vexNum; i++) {
		if (i != firstPoint) {
			distance[i] = this->m_adjMatrix[firstPoint][i];
		}
	}

	for (i = 0; i < this->m_vexNum; i++) {
		if (i != firstPoint) {
			min = EDGEDISTANCE_MAN;
			tempPoint = 0;
			for (j = 0; j < this->m_vexNum; j++) {
				if (book[j] == false && distance[j] < min) {
					min = distance[j];
					tempPoint = j; // 记录最短弧的终点
				}
			}



			book[tempPoint] = true; //将最短弧的终点/弧头加入集合

			for (j = 0; j < this->m_vexNum; j++) {
				if (book[j] == false) { //如果顶点j在集合Book中
					// 如果从p点到j点有弧,且从起点到j点的已有路径长度大于从起点经p点中转再到j点的路径长度
					if (distance[j] > distance[tempPoint] + this->m_adjMatrix[tempPoint][j]) {
						// 则进行松弛(贪心的体现)
						distance[j] = distance[tempPoint] + this->m_adjMatrix[tempPoint][j];
					}
				}
			}
		}
	}

	delete[] book;
	book = nullptr;
}

时间复杂度：$O(n^2)$

主函数

负责创建AdjMatrixGharp类型的对象，进行Dijkstra操作求出最短路径，并打印出来

int main()
{
	int n;
	std::cout << "Please enter the number of points on the next line: " << std::endl;
	std::cin >> n;
	// 创建行和列都为 n 的邻接矩阵
	AdjMatrixGraph g(n);
	std::cout << "Dang Dang!! The adjacent matrix was successfully created" << std::endl;
	// 申请堆内存，用于存放原点到各个点的最短路径
	int* distanceList = nullptr;
	int* path = nullptr;
	distanceList = new int[n];
	path = new int[n];
	if (distanceList == nullptr || path == nullptr) { // 错误检测
		std::cerr << "Malloc Error!" << std::endl;
	}

	// Dijkstra算法求最短路径
	g.Dijkstra(0, distanceList);

	// 输出 distanceList 数组
	std::cout << "The shortest distance between firstPoint and secondPoint" << std::endl;
	for (int i = 0; i < n; i++) {
		std::cout << distanceList[i] << std::endl;
	}

	// 释放 distanceList
	if (distanceList != nullptr) {
		delete[] distanceList;
		distanceList = nullptr;
	}
}

四、使用说明、测试分析及结果

1. 说明如何使用你编写的程序

先输入一个小于 100 的正整数 n

然后输入图的邻接矩阵（10000 表示无穷大，即两点之间没有边）

最后输入两个 0 到 n-1 的整数表示两个点。

2. 测试结果与分析

本实验的时间复杂度为：

• 邻接矩阵的构造函数：$O(n^2)$
• 邻接矩阵的析构函数：$O(n^2)$
• 邻接矩阵的Dijkstra算法：$O(n^2)$

故总时间复杂度为：$O(n^2)$

这里的n指的是该无向图点的个数

3. 调试过程中遇到的问题是如何解决提以及对设计与实现的回顾讨论和分析

1. 我在类中直接定义int m_adjMatrix[100][100]，系统会给出一个 Warning，提示这种大数组不应该存放在栈区，应该自己主动申请堆区内存或者将m_adjMatrix设置为全局变量。最后我使用了双指针来储存这个邻接矩阵，具体算法详见“邻接矩阵的构造函数”。
2. 实现Dijkstra算法时，对如何加入已遍历的点集book理解不正确，导致程序出错。其实如何确定点是否加入book点集，使用的是贪心思想，是对于某一时刻未被添加进book的点的distance最小值加入点集book

4. 运行界面

本程序的运行环境为Visual Studio Code + gcc-8.1.0

五、实验总结

1. 实验不足

利用邻接矩阵存储无向有权图的点与点之间的距离，这显然是一个对称矩阵，加上很多点之间没有边（即距离为无穷大），所以用邻接矩阵会浪费很多空间。下次做题的时候可以使用邻接表来实现点与点之间边的存储。

2. 实验优点

1. 程序采用了类的封装，避免了对象内存的直接访问，使程序更加具有普遍意义
2. 有对程序输入的引导，告诉使用者该怎样输入数据，提高了程序的交互性
3. 若程序出现错误，比如内存分配错误，会给出报错，提高了程序的可维护性
4. 程序风格统一，变量命名较为规范。
5. 用顺序表和链表两种数据结构实现该实验，充分掌握了Dijkstra算法求无向有权图的最短路径

实验 4.2

• 实验题目：实验 4.2：用迪杰斯特拉算法求赋权图中的最短路径
• 实验目的：了解无向图的最短路径算法——Dijkstra算法
• 实验内容：用迪杰斯特拉算法求一点到其余所有结点的最短路径

一、需求分析

1. 输入的形式

先输入一个小于 100 的正整数 n，然后输入图的邻接矩阵（10000 表示无穷大，即两点之间没有边），最后输入两个 0 到 n-1 的整数表示两个点

2. 输出的形式

先用迪杰斯特拉算法求给定的第一个点到其余所有结点的最短路径。然后再输出给定的两个点之间的最短路径（按顺序输出最短路径上的每一个点，每个数据占一行）

3. 程序所要达到的功能

• 用Dijkstra算法求一点到其余所有结点的最短路径
• 用Dijkstra算法求任意两点之间的最短路径

4. 测试数据

样例输入

4 
0 2 10 10000
2 0 7 3 
10 7 0 6
10000 3 6 0
0 2 

样例输出

0 
1 
2

二、概要设计

1. 用邻接矩阵记录一个无向图（是一个对称矩阵）
2. 对该无向图利用Dijkstra算法求出原点到其他点的最短路径，在这过程中，用path数组记录某一点的前一节点
3. 输出给定的两个点之间的最短路径（按顺序输出最短路径上的每一个点）

基本操作

以邻接矩阵为存储结构的无向图

用于储存具体数据（点的个数、点与点之间的距离）

class AdjMatrixGraph
{
public:
	AdjMatrixGraph(int n); // 构造函数
	~AdjMatrixGraph(); // 析构函数
	void Dijkstra(int firstPoint, int* distanceList, int* path) const; // Dijkstra算法
private:
	int** m_adjMatrix; // 邻阶矩阵
	int m_vexNum; // 点的个数
};

distanceList数组

用于储存源点到各个点的距离

析构函数——初始化邻接矩阵

AdjMatrixGraph::AdjMatrixGraph(int n)

析构函数——销毁邻接矩阵

AdjMatrixGraph::~AdjMatrixGraph()

Dijkstra算法——最短路径算法

期中path数组用来保存每一节点的前面一节点，若没有前面的节点，其值为 -1

void AdjMatrixGraph::Dijkstra(int firstPoint, int* distanceList, int* path) const

程序调用图

解释：

• 粗线表示程序总的流程
• 细线表示一些函数与变量或对象的调用关系
• 方括号表示变量或对象
• 棱形表示函数
• 圆表示一个变量（结构体，数组）

三、详细设计

我们以样例为例，探究如何完成这道实验题

样例输入：

4 
0 2 10 10000
2 0 7 3 
10 7 0 6
10000 3 6 0
0 2 

样例输出：

0 
1 
2

分析样例

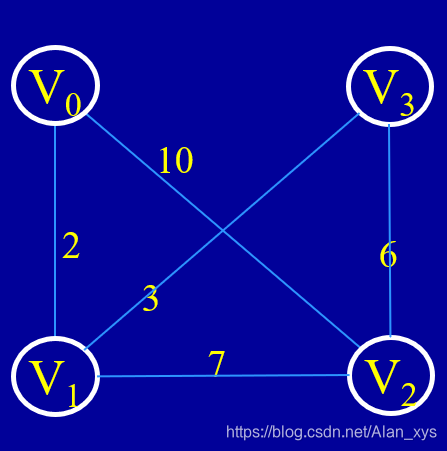
依题意，求顶点v0到其他各点的最短路径

首先第一步，我们先声明一个path数组，该数组初始化的值为

-1 0 0 -1

这里，-1表示两个点之间不连通，其他数字代表该点的前一个节点是什么

当然，我们还得声明一个distance数组，该数组初始化的值为

0 2 10 INF

这里INF的大小为10000，表示两个点之间不连通

我们的顶点集book的初始化为：book = {v0} （若点对应book数组中的值为true时，代表在点集内）

既然是求 v0 顶点到其余各个顶点的最短路程，那就先找一个离 0 号顶点最近的顶点。通过数组 distance 可知当前离v0 顶点最近是 v1 顶点。当选择了 1 号顶点后，distance[1]（下标从0开始）的值就已经从“估计值”变为了“确定值”，即 v0 顶点到 v1 顶点的最短路程就是当前 dis[1]值。将v1加入到 book 中。
为什么呢？因为目前离 v0 顶点最近的是 v1顶点，并且这个图所有的边都是正数，那么肯定不可能通过第三个顶点中转，使得 v0 顶点到 v1 顶点的路程进一步缩短了。因为 v0 顶点到其它顶点的路程肯定没有 v0 到 v1 顶点短.

OK，既然确定了一个顶点的最短路径，所以更新distance[1]的值,得到如下结果：

0 2 9 5

更新path数组，得到如下结果

-1 0 1 1

继续重复上述步骤即可

最后我们会得到

distance数组中的值：

0 2 9 5

path数组的值：

-1 0 1 1

即我们应输出的数组

此后，我们在main函数中，利用“前溯”的方法将答案输入到outputPoint数组中。

outputPoint数组中的最终结果为：

0 1 2

邻接矩阵的构造函数

这里的先初始化类成员变量m_vexNum

再为二维指针申请内存空间

最后读入数据到m_adjMatrix，完成类的初始化

djMatrixGraph::AdjMatrixGraph(int n) :m_vexNum(n)
{
	this->m_adjMatrix = new int* [n];
	for (int i = 0; i < n; i++) {
		this->m_adjMatrix[i] = new int[n];
	}
	std::cout << "Please enter the adjacent matrix of the graph" << std::endl;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			std::cin >> this->m_adjMatrix[i][j];
		}
	}
}

时间复杂度：$O(n^2)$

邻接矩阵的析构函数

对于一个由二维指针申请的堆空间的释放

AdjMatrixGraph::~AdjMatrixGraph()
{
	// 二维指针的析构
	for (int i = 0; i < this->m_vexNum; i++) {
		delete[] this->m_adjMatrix[i];
		this->m_adjMatrix[i] = nullptr;
	}
	delete[] this->m_adjMatrix;
	this->m_adjMatrix = nullptr;
}

时间复杂度：$O(n^2)$

Dijkstra算法

注：EDGEDISTANCE_MAN表示两个点之间没有边（其值为10000）

Dijkstra（迪杰斯特拉）提出了一个按路径长度递增的次序产生最短路径的算法（贪心算法）：

? 首先，引入辅助向量D，它的每个分量D[i]表示当前所找到的从始点v0到每个找到vi的最短路径的长度。它的初始状态为：若从v0到vi有弧，则D[i]为弧上的权值；否则为无穷大。显然长度为

D[j] = Min { D[i] | $v_i\in V$}

的路径就是从v出发的长度最短的一条路径，此路径为(v,vj)。

? 那么下一条长度次短的最短路径是哪一条呢？假设该次短路径的终点是vk, 则这条路径或者是(v, vk)，或者是(v, vj, vk)。 一般情况下，假设S为已求得最短路径的终点的集合，可以使用该算法。

void AdjMatrixGraph::Dijkstra(int firstPoint, int* distance, int* path) const
{
	int tempPoint; // 临时的点，记录上一个遍历的点
	int min, i, j;
	bool* book = new bool[this->m_vexNum]; // 一个点集，用于存放已经确定最短路径的点
	
	// 初始化各数组
	for (int i = 0; i < this->m_vexNum; i++) {
		book[i] = false; // 这时还未遍历任何一个点
		distance[i] = EDGEDISTANCE_MAN;
	}

	/*  已遍历源点，且源点到源点的距离为0 */
	book[firstPoint] = true; // 将起点加入集合
	distance[firstPoint] = 0; // 起点到自己的距离为0 //
	path[firstPoint] = -1;

	// 对从原点出发的边进行统计
	for (i = 0; i < this->m_vexNum; i++) {
		if (i != firstPoint) {
			distance[i] = this->m_adjMatrix[firstPoint][i];
			if (distance[i] < EDGEDISTANCE_MAN) {
				path[i] = firstPoint; //如果起点firstPoint与结点i之间存在边，则i的上一个结点就是 firstPoint
			}
			else {
				path[i] = -1; //如果起点 firstPoint 与结点 i 之间不存在边，给path[i]赋值 -1
			}
		}
	}

	for (i = 0; i < this->m_vexNum; i++) {
		if (i != firstPoint) {
			min = EDGEDISTANCE_MAN;
			tempPoint = 0;
			for (j = 0; j < this->m_vexNum; j++) {
				if (book[j] == false && distance[j] < min) {
					min = distance[j];
					tempPoint = j; // 记录最短弧的终点
				}
			}

			book[tempPoint] = true; //将最短弧的终点/弧头加入集合

			for (j = 0; j < this->m_vexNum; j++) {
				if (book[j] == false) { //如果顶点j在集合Book中
					// 如果从p点到j点有弧,且从起点到j点的已有路径长度大于从起点经p点中转再到j点的路径长度
					if (distance[j] > distance[tempPoint] + this->m_adjMatrix[tempPoint][j]) {
						// 则进行松弛(贪心的体现)
						distance[j] = distance[tempPoint] + this->m_adjMatrix[tempPoint][j];
						path[j] = tempPoint; // 跟新path， 使 j 前一个节点为 tempPoint
					}
				}
			}
		}
	}

	delete[] book;
	book = nullptr;
}

主函数

int main()
{
	int n;
	std::cout << "Please enter the number of points on the next line: " << std::endl;
	std::cin >> n;
	// 创建行和列都为 n 的邻接矩阵
	AdjMatrixGraph g(n);
	std::cout << "Dang Dang!! The adjacent matrix was successfully created" << std::endl;
	// 申请堆内存，用于存放原点到各个点的最短路径
	int* distanceList = nullptr;
	int* path = nullptr;
	distanceList = new int[n];
	path = new int[n];
	if (distanceList == nullptr || path == nullptr) { // 错误检测
		std::cerr << "Malloc Error!" << std::endl;
	}

	int firstPoint, secondPoint;
	std::cout << "Please enter the \"first point\" and \"second point\" in the next line:" << std::endl;
	std::cin >> firstPoint >> secondPoint;

	// Dijkstra算法求最短路径
	g.Dijkstra(firstPoint, distanceList, path);

	int tempPoint = secondPoint; // 对下方 path 数组进行查找的临时变量
	int count = 0; // 记录从 firstPoint 到 secondPoint 要经过几个点
	int* outputPoint = new int[n];
	// 我们要从secondPoint开始，对path数组进行 “前溯”
	while (tempPoint != -1) {
		outputPoint[count] = tempPoint;
		tempPoint = path[tempPoint];
		count++;
	}
	
	count--; // 这里做一个调整，使得count指向outputPoint的最后一个元素

	// 输出从 firstPoint 到 secondPoint 依次经过的点
	std::cout << "The point at which the output passes from firstPoint to secondPoint" << std::endl;
	while (count > -1) {
		std::cout << outputPoint[count] << std::endl;
		count--;
	}

	// 释放 distanceList
	if (distanceList != nullptr) {
		delete[] distanceList;
		distanceList = nullptr;
	}
	// 释放 path
	if (path != nullptr) {
		delete[] path;
		path = nullptr;
	}
	// 释放 outputPoint
	if (outputPoint != nullptr) {
		delete[] outputPoint;
		outputPoint = nullptr;
	}
}

四、使用说明、测试分析及结果

1. 说明如何使用你编写的程序

先输入一个小于 100 的正整数 n

然后输入图的邻接矩阵（10000 表示无穷大，即两点之间没有边）

最后输入两个 0 到 n-1 的整数表示两个点。

2. 测试结果与分析

本实验的时间复杂度为：

• 邻接矩阵的构造函数：$O(n^2)$
• 邻接矩阵的析构函数：$O(n^2)$
• 邻接矩阵的Dijkstra算法：$O(n^2)$

故总时间复杂度为：$O(n^2)$

这里的n指的是该无向图点的个数

3. 调试过程中遇到的问题是如何解决提以及对设计与实现的回顾讨论和分析

1. 我在类中直接定义int m_adjMatrix[100][100]，系统会给出一个 Warning，提示这种大数组不应该存放在栈区，应该自己主动申请堆区内存或者将m_adjMatrix设置为全局变量。最后我使用了双指针来储存这个邻接矩阵，具体算法详见“邻接矩阵的构造函数”。
2. 实现Dijkstra算法时，对如何加入已遍历的点集book理解不正确，导致程序出错。其实如何确定点是否加入book点集，使用的是贪心思想，是对于某一时刻未被添加进book的点的distance最小值加入点集book
3. 虽然我们得到了每个节点的前一个节点path数组，但是这并不是答案所要求的形式，最后我采用前溯的方法，利用path数组“向前”迭代遍历，得到outputPoint数组，最后倒叙输出即为正确答案

4. 运行界面

本程序的运行环境为Visual Studio Code + gcc-8.1.0

五、实验总结

1. 实验不足

利用邻接矩阵存储无向有权图的点与点之间的距离，这显然是一个对称矩阵，加上很多点之间没有边（即距离为无穷大），所以用邻接矩阵会浪费很多空间。下次做题的时候可以使用邻接表来实现点与点之间边的存储。

2. 实验优点

1. 程序采用了类的封装，避免了对象内存的直接访问，使程序更加具有普遍意义
2. 有对程序输入的引导，告诉使用者该怎样输入数据，提高了程序的交互性
3. 若程序出现错误，比如内存分配错误，会给出报错，提高了程序的可维护性
4. 程序风格统一，变量命名较为规范。
5. 用顺序表和链表两种数据结构实现该实验，充分掌握了Dijkstra算法求无向有权图的最短路径

实验 4.3

• 实验题目：实验 4.3：用弗洛伊德算法求赋权图的两点间的最短路径的长度
• 实验目的：了解无向图的最短路径算法——Floyd算法
• 实验内容：用弗洛伊德算法求一点到其余所有结点的最短路径

一、需求分析

1. 输入的形式

先输入一个小于 100 的正整数 n，然后输入图的邻接矩阵（10000 表示无穷大，即两点之间没有边），之后再输入一个小于100的正整数m，最后m行每行输入两个不同的0到n-1之间的整数表示两个点

2. 输出的形式

先用弗洛伊德算法求给定的第一个点到其余所有结点的最短路径。并输出这些两个点之间的最短路径的长度

3. 程序所要达到的功能

用Floyd算法求一点到其余所有结点的最短路径

4. 测试数据

样例输入：

4
0 2 10 10000
2 0 7 3
10 7 0 6
10000 3 6 0
2
0 2
3 0

样例输出：

9
5

二、概要设计

1. 用邻接矩阵记录一个无向图（是一个对称矩阵）
2. 对该无向图利用Floyd算法求出原点到其他点的最短路径（利用一个n*n的矩阵记录两点间的最短路径）
3. 依次输出两点间的最短路径

基本操作

以邻接矩阵为存储结构的无向图

用于储存具体数据（点的个数、点与点之间的距离）

class AdjMatrixGraph
{
public:
	AdjMatrixGraph(int n); // 构造函数
	~AdjMatrixGraph(); // 析构函数
	void Floyd(int** distance, int** path) const; // Floyd算法
private:
	int** m_adjMatrix; // 邻阶矩阵
	int m_vexNum; // 点的个数
};

distanceList[][]数组

用于储存一个点到另一个点的最短距离，是一个二维数组，distance[i][j]表示点 i 到点 j 的最短距离

path[][]

用来储存每个点到其他点最短距离的路径

要点：以每个点为「中转站」，刷新所有「入度」和「出度」的距离。
所以我们要：遍历每一个顶点 --> 遍历点的每一个入度 --> 遍历每一个点的出度，以这个点为「中转站」距离更短就刷新距离（比如 B 点为中转站 AB + BD < AD 就刷新 A 到 D 的距离）

析构函数——初始化邻接矩阵

AdjMatrixGraph::AdjMatrixGraph(int n)

析构函数——销毁邻接矩阵

AdjMatrixGraph::~AdjMatrixGraph()

Dijkstra算法——最短路径算法

void AdjMatrixGraph::Floyd(int** distance, int** path) const; // Floyd算法

程序调用图

解释：

• 粗线表示程序总的流程
• 细线表示一些函数与变量或对象的调用关系
• 方括号表示变量或对象
• 棱形表示函数
• 圆表示一个变量（结构体，数组）

三、详细设计

我们以样例为例，探究如何完成这道实验题

样例输入：

6 
0 1 4 10000 10000 10000
1 0 2 7 5 10000
4 2 0 10000 1 10000
10000 7 10000 0 3 2
10000 5 1 3 0 6
10000 10000 10000 2 6 0

样例输出：

0
1
3
7
4
9

分析样例

我太懒了，大家直接看这篇文章好了

Dijkstra算法详解 通俗易懂

邻接矩阵的构造函数

这里的先初始化类成员变量m_vexNum

再为二维指针申请内存空间

最后读入数据到m_adjMatrix，完成类的初始化

djMatrixGraph::AdjMatrixGraph(int n) :m_vexNum(n)
{
	this->m_adjMatrix = new int* [n];
	for (int i = 0; i < n; i++) {
		this->m_adjMatrix[i] = new int[n];
	}
	std::cout << "Please enter the adjacent matrix of the graph" << std::endl;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			std::cin >> this->m_adjMatrix[i][j];
		}
	}
}

时间复杂度：$O(n^2)$

邻接矩阵的析构函数

对于一个由二维指针申请的堆空间的释放

AdjMatrixGraph::~AdjMatrixGraph()
{
	// 二维指针的析构
	for (int i = 0; i < this->m_vexNum; i++) {
		delete[] this->m_adjMatrix[i];
		this->m_adjMatrix[i] = nullptr;
	}
	delete[] this->m_adjMatrix;
	this->m_adjMatrix = nullptr;
}

时间复杂度：$O(n^2)$

Floyd算法

void AdjMatrixGraph::Floyd(int** distance, int** path) const
{
	for (int i = 0; i < this->m_vexNum; i++) {
		for (int j = 0; j < this->m_vexNum; j++) {
			distance[i][j] = this->m_adjMatrix[i][j];
		}
	}

	for (int i = 0; i < this->m_vexNum; i++) {
		for (int j = 0; j < this->m_vexNum; j++) {
			path[i][j] = -1;
		}
	}

	for (int i = 0; i < this->m_vexNum; i++) {
		for (int j = 0; j < this->m_vexNum; j++) {
			for (int k = 0; k < this->m_vexNum; k++) {
				if (distance[j][k] > distance[j][i] + distance[i][k]) {
					distance[j][k] = distance[j][i] + distance[i][k];
					path[j][k] = i;
				}
			}
		}
	}
}

时间复杂度：$O(n^3)$，空间复杂度：$O(n^2)$

主函数

负责创建AdjMatrixGharp类型的对象，进行Floyd操作求出最短路径，并打印出来

int main()
{
	int n;
	std::cin >> n;
	int** distance, ** path;
	// distance 的内存申请（二维指针的内存申请）
	distance = new int* [n];
	for (int i = 0; i < n; i++) {
		distance[i] = new int[n];
	}
	// path 的内存申请
	path = new int* [n];
	for (int i = 0; i < n; i++) {
		path[i] = new int[n];
	}


	AdjMatrixGraph graph(n);
	graph.Floyd(distance, path);

	int outNum;
	std::cin >> outNum;
	int firstPos, secondPos;
    while (outNum--) {
    	std::cin >> firstPos >> secondPos;
    	std::cout << distance[firstPos][secondPos] << std::endl;
    }

	// distance 的内存释放（二维指针的析构）
	for (int i = 0; i < n; i++) {
		delete[] distance[i];
		distance[i] = nullptr;
	}

	delete[] distance;
	distance = nullptr;
	// path 的内存释放
	for (int i = 0; i < n; i++) {
		delete[] path[i];
		path[i] = nullptr;
	}

	delete[] path;
	path = nullptr;
	// outPoint 的内存释放
	delete[] outputPoint;
	outputPoint = nullptr;
}

四、使用说明、测试分析及结果

1. 说明如何使用你编写的程序

先输入一个小于 100 的正整数 n

然后输入图的邻接矩阵（10000 表示无穷大，即两点之间没有边）

最后输入若干组两个点。

2. 测试结果与分析

本实验的时间复杂度为：

• 邻接矩阵的构造函数：$O(n^2)$
• 邻接矩阵的析构函数：$O(n^2)$
• 邻接矩阵的Floyd算法：$O(n^3)$

故总时间复杂度为：$O(n^3)$

这里的n指的是该无向图点的个数

空间复杂度：$O(n^2)$

3. 调试过程中遇到的问题是如何解决提以及对设计与实现的回顾讨论和分析

1. 我在类中直接定义int m_adjMatrix[100][100]，系统会给出一个 Warning，提示这种大数组不应该存放在栈区，应该自己主动申请堆区内存或者将m_adjMatrix设置为全局变量。最后我使用了双指针来储存这个邻接矩阵，具体算法详见“邻接矩阵的构造函数”。

4. 运行界面

本程序的运行环境为Visual Studio Code + gcc-8.1.0

五、实验总结

本题编程用时1小时，因为本题的核心算法为弗洛伊德算法，所以在编程时大多数时间投入到对算法的理解上。弗洛伊德算法的简洁性让我觉得它非常的优美，而其本质的想法就是不断的从中转点进行切换，并与对原先的路径进行比较，如果大于原先的路径，则将更短的路径进行覆盖，所以只需要对每一个顶点进行一一的比对，就可以找到最短的路径。算法唯一的缺点就是时间复杂度较高，让其处理大量的数据会降低效率，所以要具体问题具体分析。最大的收获便是认识到了又一个简洁的代码解决了一个复杂的问题。

实验优点

1. 程序采用了类的封装，避免了对象内存的直接访问，使程序更加具有普遍意义
2. 有对程序输入的引导，告诉使用者该怎样输入数据，提高了程序的交互性
3. 若程序出现错误，比如内存分配错误，会给出报错，提高了程序的可维护性
4. 程序风格统一，变量命名较为规范。
5. 用顺序表和链表两种数据结构实现该实验，充分掌握了Floyd算法求无向有权图的最短路径

实验4.4

做法也是调用实验3.3中的Floyd函数

实验3.3写得已经比较详细了，这里仅给出main()函数

int main()
{
	int n;
	std::cin >> n;
	int** distance, ** path;
	// distance 的内存申请（二维指针的内存申请）
	distance = new int* [n];
	for (int i = 0; i < n; i++) {
		distance[i] = new int[n];
	}
	// path 的内存申请
	path = new int* [n];
	for (int i = 0; i < n; i++) {
		path[i] = new int[n];
	}


	AdjMatrixGraph graph(n);
	graph.Floyd(distance, path);

	int outNum;
	std::cin >> outNum;
	int firstPos, secondPos;

	int count, tempPoint;
	int* outputPoint = new int[n];
	while (outNum--) {
		std::cin >> firstPos >> secondPos;
		count = 1;
		outputPoint[0] = secondPos;
		tempPoint = secondPos;
		while (true) {
			tempPoint = path[firstPos][tempPoint];
			
			if (tempPoint == firstPos || tempPoint == -1) {
				outputPoint[count] = firstPos;
				break;
			}
			outputPoint[count] = tempPoint;
			count++;
		}

		while (count > -1) {
			std::cout << outputPoint[count] << std::endl;
			count--;
		}
	}
	// distance 的内存释放（二维指针的析构）
	for (int i = 0; i < n; i++) {
		delete[] distance[i];
		distance[i] = nullptr;
	}

	delete[] distance;
	distance = nullptr;
	// path 的内存释放
	for (int i = 0; i < n; i++) {
		delete[] path[i];
		path[i] = nullptr;
	}

	delete[] path;
	path = nullptr;
	// outPoint 的内存释放
	delete[] outputPoint;
	outputPoint = nullptr;
}

充分掌握了Floyd算法求无向有权图的最短路径

实验4.4

做法也是调用实验3.3中的Floyd函数

实验3.3写得已经比较详细了，这里仅给出main()函数

int main()
{
	int n;
	std::cin >> n;
	int** distance, ** path;
	// distance 的内存申请（二维指针的内存申请）
	distance = new int* [n];
	for (int i = 0; i < n; i++) {
		distance[i] = new int[n];
	}
	// path 的内存申请
	path = new int* [n];
	for (int i = 0; i < n; i++) {
		path[i] = new int[n];
	}


	AdjMatrixGraph graph(n);
	graph.Floyd(distance, path);

	int outNum;
	std::cin >> outNum;
	int firstPos, secondPos;

	int count, tempPoint;
	int* outputPoint = new int[n];
	while (outNum--) {
		std::cin >> firstPos >> secondPos;
		count = 1;
		outputPoint[0] = secondPos;
		tempPoint = secondPos;
		while (true) {
			tempPoint = path[firstPos][tempPoint];
			
			if (tempPoint == firstPos || tempPoint == -1) {
				outputPoint[count] = firstPos;
				break;
			}
			outputPoint[count] = tempPoint;
			count++;
		}

		while (count > -1) {
			std::cout << outputPoint[count] << std::endl;
			count--;
		}
	}
	// distance 的内存释放（二维指针的析构）
	for (int i = 0; i < n; i++) {
		delete[] distance[i];
		distance[i] = nullptr;
	}

	delete[] distance;
	distance = nullptr;
	// path 的内存释放
	for (int i = 0; i < n; i++) {
		delete[] path[i];
		path[i] = nullptr;
	}

	delete[] path;
	path = nullptr;
	// outPoint 的内存释放
	delete[] outputPoint;
	outputPoint = nullptr;
}