[数据结构与算法]63 不同路径-02

63 不同路径-02

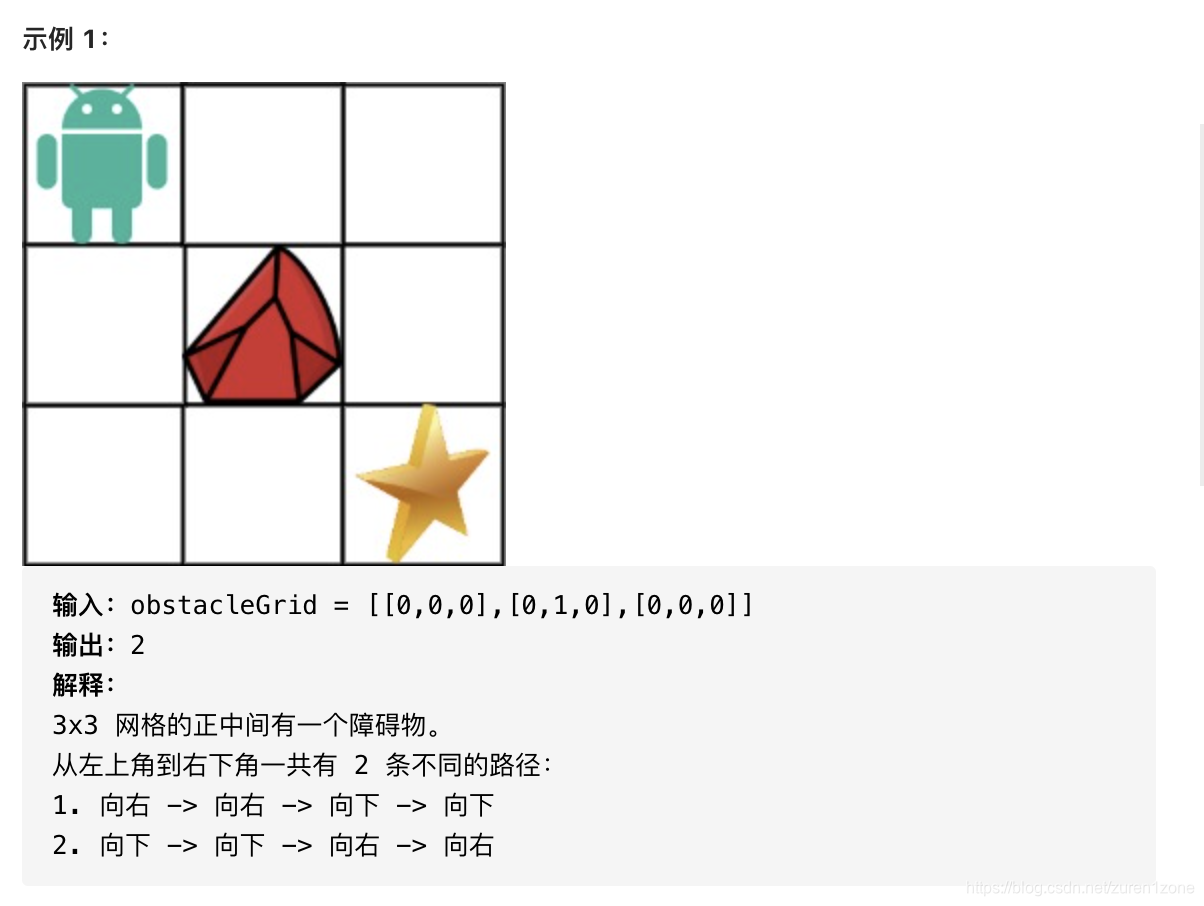
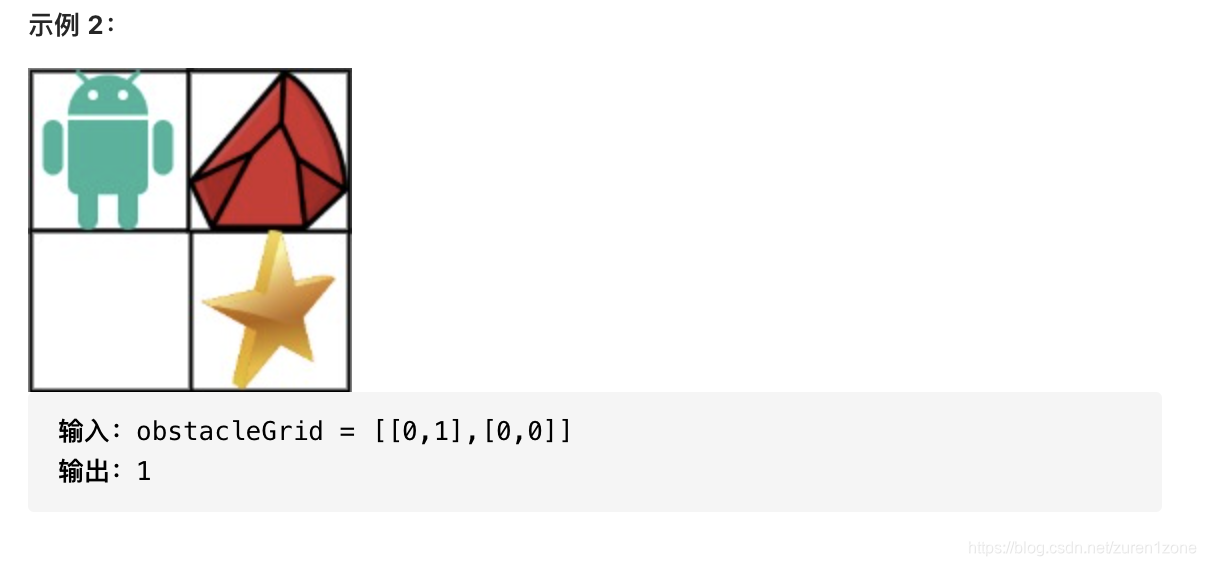
动态规划

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int rows = obstacleGrid.length;
        int colums = obstacleGrid[0].length;
        int[][] f = new int[rows][colums];
        for(int i=0;i<rows;i++){
            Arrays.fill(f[i],0);
        }
        if(obstacleGrid[0][0]==0){
            f[0][0] = 1;
        }
        

        for(int i=0;i<rows;i++){
            for(int j=0;j<colums;j++){
                if(i+1<rows && obstacleGrid[i+1][j]==0){
                    f[i+1][j]+=f[i][j];
                }
                if(j+1<colums && obstacleGrid[i][j+1]==0){
                    f[i][j+1] += f[i][j];
                }
            }
        } 

        return f[rows-1][colums-1];

    }
}

时间复杂度$O(mn)$。
空间复杂度$O(mn)$。

优化空间

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int rows = obstacleGrid.length;
        int colums = obstacleGrid[0].length;
        int[] f = new int[colums];
        Arrays.fill(f,0);
        // for(int i=0;i<rows;i++){
        //     Arrays.fill(f[i],0);
        // }
        if(obstacleGrid[0][0]==0){
            f[0] = 1;
        }
        

        for(int i=0;i<rows;i++){
            for(int j=0;j<colums;j++){
                if(obstacleGrid[i][j]!=0){
                    f[j] = 0;
                    continue;
                }
                // if(i+1<rows && obstacleGrid[i+1][j]!=0){
                //     f[j] = 0;
                // }
                if(j+1<colums && obstacleGrid[i][j+1]==0){
                    f[j+1] += f[j];
                }
            }
        } 

        return f[colums-1];

    }
}

时间复杂度$O(mn)$。
空间复杂度$O(n)$。