[数据结构与算法]从零开始学习数据结构与算法（10）—— 树

1.为什么需要树这种结构？

数组存储方式的分析：
数组扩容：每次在底层都需要创建新的数组，要将原来的数据拷贝到数组，并插入数据

2.二叉树的概念和常用术语

2.1 基本概念

2.2 二叉树的概念

1）树有很多种，每个节点最多只能有两个子节点的一种形式称为二叉树
2）二叉树的子节点分为左节点和右节点
3）如果该二叉树的叶子节点都在最后一层，并且节点总数=2^n-1，n为层数，则我们称为满二叉树
4）如果该二叉树的所有叶子节点都在最后一层或者倒数第二层，而且最后一层的叶子节点在左边连续，倒数第二层的叶子节点在右边连续，我们称为完全二叉树

2.2.1 创建二叉树节点

//创建节点
class HeroNode{
    private int no;
    private String name;
    private HeroNode left;//默认null
    private HeroNode right;//默认null

    public HeroNode(int no, String name) {
        this.no = no;
        this.name = name;
    }

    public int getNo() {
        return no;
    }

    public void setNo(int no) {
        this.no = no;
    }

    public String getName() {
        return name;
    }

    public void setName(String name) {
        this.name = name;
    }

    public HeroNode getLeft() {
        return left;
    }

    public void setLeft(HeroNode left) {
        this.left = left;
    }

    public HeroNode getRight() {
        return right;
    }

    public void setRight(HeroNode right) {
        this.right = right;
    }

    @Override
    public String toString() {
        return "HeroNode{" +
                "no=" + no +
                ", name='" + name + '\'' +
                '}';
    }
}

2.2.2 创建二叉树

//定义二叉树
class BinaryTree{
    private HeroNode root;

    public void setRoot(HeroNode root) {
        this.root = root;
    }
}

3.二叉树的遍历

前序遍历：先输出父节点，再遍历左子树和右子树。
中序遍历：先遍历左子树，再输出父节点再遍历右子树。
后序遍历：先遍历左子树，再遍历右子树，最后输出父节点。

前序遍历步骤：
1.先输出当前节点；
2.如果左子节点不为空，则递归继续前序遍历；
3.如果右子节点不为空，则递归继续前序遍历。

中序遍历步骤：
1.如果当前节点的左子节点不为空，则递归中序遍历；
2.输出当前这个节点；
3.如果当前节点的右子节点不为空，则递归中序遍历。

后序遍历步骤：
1.如果当前节点的左子节点不为空，则递归后序遍历；
2.如果当前节点的右子节点不为空，则递归后序遍历；
3.输出当前节点。

//向二叉树类BinaryTree中添加方法
//****************************遍历******************************
    //前序遍历
    public void preOrder(){
        if(this.root != null){
            this.root.preOrder();
        }else{
            System.out.println("二叉树为空,无法遍历");
        }
    }

    //中序遍历
    public void infixOrder(){
        if (this.root != null){
            this.root.infixOrder();
        }else{
            System.out.println("二叉树为空，无法遍历");
        }
    }

    //后序遍历
    public void postOrder(){
        if (this.root != null){
            this.root.postOrder();
        }else{
            System.out.println("二叉树为空，无法遍历");
        }
    }

//向节点类HeroNode中添加方法
//********************************遍历*******************************
    //编写前序遍历的方法
    public  void preOrder(){
        System.out.println(this);//先输出父节点
        //向左子树递归前序遍历
        if (this.left != null){
            this.left.preOrder();
        }
        //向右子树递归前序遍历
        if (this.right != null){
            this.right.preOrder();
        }
    }

    //编写后序遍历的方法
    public void infixOrder(){
        //向左子树递归中序遍历
        if (this.left != null){
            this.left.infixOrder();
        }
        //输出父节点
        System.out.println(this);
        //向右子树递归中序遍历
        if (this.right != null){
            this.right.infixOrder();
        }
    }

    //编写后序遍历的方法
    public void postOrder() {
        //向左子树递归后序遍历
        if (this.left != null) {
            this.left.postOrder();
        }
        //向左子树递归后序遍历
        if (this.right != null) {
            this.right.postOrder();
        }
        //输出当前父节点
        System.out.println(this);
    }

4. 二叉树的查找

前序查找步骤：
1.先判断当前节点是否是要查找的节点，如果相等，则返回当前节点；
2.如果不相等，则判断当前节点；左子节点是否为空，如果不为空，则递归前序查找；
3.若左递归前序查找找到了待查找的节点则返回，否则判断当前节点的右节点是否为空，如果不空，则向右递归前序查找。找到则返回，否则返回null。

中序查找步骤：
1.判断当前节点的左子节点是否为空，如果不为空，则向左递归查找，若找到了则返回节点；
2.如果没有找到则与当前节点进行比较，如果当前节点是待查找节点则返回此节点；
3.否则判断右子节点是否为空，若不为空，则向右递归中序查找。找到则返回，否则返回null。

后序查找步骤：
1.判断当前节点的左子节点是否为空，如果不为空，则向左递归查找，若找到了则返回节点；
2.若没有找到，则判断当前节点的右子节点是否为空，若不为空，则右递归进行后序查找，若找到则返回，没找到就和当前节点进行比较，若相同，则返回当前节点，否则返回null。

//向二叉树类BinaryTree中添加代码
//*********************查找***************************
    //前序遍历查找
    public HeroNode preOrderSearch(int no){
        if (root != null){
            return root.preOrderSearch(no);
        }else{
            return null;
        }
    }
    //中序遍历查找
    public HeroNode infixOrderSearch(int no){
        if (root != null){
            return this.root.infixOrderSearch(no);
        }else{
            return null;
        }
    }
    //后序遍历查找
    public HeroNode postOrderSearch(int no){
        if (root != null){
            return this.root.postOrderSearch(no);
        }else{
            return null;
        }
    }

//向节点类HeroNode类中添加代码
//*****************************查找***************************
    //前序遍历查找
    public HeroNode preOrderSearch(int no){
        System.out.println("进入前序查找");
        //比较当前节点是不是查找节点
        if (this.no == no){
            return this;
        }
        //1.判断当前节点的左子节点是否为空，如果不为空，则递归前序查找
        //2.如果左递归前序查找，找到节点，则返回
        HeroNode resNode = null;
        if (this.left != null){
            resNode = this.left.preOrderSearch(no);
        }
        if (resNode != null){
            return resNode;
        }
        //1.左递归前序查找找到节点，则返回,否则继续判断
        //2.当前节点右节点是否为空，不为空向右递归,找到则返回，否则返回null
        if (this.right != null){
            resNode = this.right.preOrderSearch(no);
        }
        return resNode;
    }

    //中序遍历查找
    public HeroNode infixOrderSearch(int no){
        //判断当前节点的左子节点是否为空，非空则向左递归中序查找,找到则返回，否则判断当前节点
        HeroNode resNode = null;
        if (this.left != null){
            resNode = this.left.infixOrderSearch(no);
        }
        if (resNode != null){
            return resNode;
        }
        //判断当前节点
        System.out.println("进入中序查找");
        if (this.no == no){
            return this;
        }
        //判断当前节点的右子节点
        if (this.right != null){
            resNode = this.right.infixOrderSearch(no);
        }
        return resNode;
    }

    //后序遍历查找
    public HeroNode postOrderSearch(int no){
        System.out.println("111");
        //判断当前节点的左子节点是否为空，非空则向左递归中序查找,找到则返回，否则判断右节点是否为空
        HeroNode resNode = null;
        if (this.left != null){
            resNode = this.left.postOrderSearch(no);
        }
        if (resNode != null){//左子树找到
            return resNode;
        }
        //判断右子节点是否为空
        if (this.right != null){//左子树每找到向右递归
            resNode = this.right.postOrderSearch(no);
        }
        if (resNode != null){//右子树找到
            return resNode;
        }
        System.out.println("进入后序查找");
        //判断当前节点
        if (this.no == no){
            return this;
        }
        return resNode;
    }

5.二叉树的删除

完成删除节点的操作：
1）如果删除的节点是叶子节点，则删除该节点；
2）如果删除的节点是非叶子节点，则删除该树。

思路：
首先先处理：
考虑如果树是空树root，如果只有一个root节点则等价于将二叉树置空。
再处理：
1.因为我们的二叉树是单向的，所以我们是判断当前节点的子节点是否是需要删除的节点，而不能判断当前这个节点是否是需要删除的节点；
2.如果当前节点的左子节点不为空，并且左子节点就是要删除的节点，则this.left = null;并且返回（结束递归删除）；
3.如果当前节点的右子节点不为空，并且右子节点就是要删除节点，则this.right = null;并且返回（结束递归删除）；
4.如果第2、3步没有完成，那么我们就需要向左子树进行递归删除；
5.如果第4步没有完成，则向右子树进行递归删除；

//向二叉树类中添加代码
//*************************删除节点*************************
    public void delNode(int no){
        if (this.root != null){
            //如果只有一个root节点，判断root节点是不是要删除的节点
            if (root.getNo() == no){
                root = null;
            }else{
                //递归删除
                root.delNode(no);
            }
        }else {
            System.out.println("空树无法删除");
        }
    }

//向节点类HeroNode中添加代码
//*******************************递归删除节点**************************
    public void delNode(int no){
        //如果当前节点的左子节点不为空，并且左子节点就是要删除的节点，就将左子节点置空
        if (this.left != null && this.left.no == no){
            this.left = null;
            return;
        }
        //如果当前节点的右子节点不为空，并且右子节点就是要删除的节点，就将右子节点置空
        if (this.right != null && this.right.no == no){
            this.right = null;
            return;
        }
        //向左子树递归
        if (this.left != null){
            this.left.delNode(no);
        }
        //向右子树递归
        if (this.right != null){
            this.right.delNode(no);
        }
    }

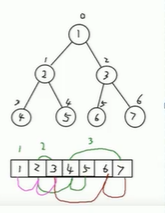
6.顺序存储二叉树

基本说明：
从数据存储来看，数组存储方式和树的存储方式可以相互转换，即数组可以转换成树，树也可以转换成数组

要求：
下图的二叉树的结点，要求以数组的方式来存放arr：[1,2,3,4,5,6]；
要求在遍历数组arr时，仍然可以以前序遍历、中序遍历、后序遍历的方式完成结点的遍历。

顺序存储二叉树的特点:
1）顺序存储二叉树通常只考虑完全二叉树
2）第n个元素的左子节点下标为2n+1
3）第n个元素的右子节点下标为2n+2
4）第n个元素的父节点为（n-1）/2
5）n表示二叉树的第几个元素（按0开始编号）

代码实现：

public class ArrayBinaryTreeDemo {
    public static void main(String[] args) {
        int[] arr = {1,2,3,4,5,6,7};
        //创建ArrayBinaryTree
        ArrayBinaryTree arrayBinaryTree = new ArrayBinaryTree(arr);
        arrayBinaryTree.preOrder();
    }
}

//编写ArrayBinaryTree，实现顺序存储二叉树遍历

class ArrayBinaryTree{
    private int[] arr;//存储数据节点的数组

    public ArrayBinaryTree(int[] arr) {
        this.arr = arr;
    }

    //编写一个方法完成顺序存储二叉树的前序遍历
    /**
     *
     * @param index 数组的下标
     */
    public void preOrder(int index){
        //如果数组为空，或者arr.length = 0
        if (arr == null || arr.length == 0){
            System.out.println("数组为空，不能按照二叉树的前序遍历");
        }
        //输出当前元素
        System.out.println(arr[index]);
        //向左递归遍历
        if((index*2)+1 < arr.length){
            preOrder(2*index + 1);
        }
        //向右递归遍历
        if ((index*2)+2 < arr.length){
            preOrder(2*index + 2);
        }
    }

    //重载preOrder
    public void preOrder(){
        this.preOrder();
    }
}

7.线索化二叉树

7.1 基本介绍

1）n个节点的二叉链表中含有（2n-（n-1））=n+1个空指针域。利用二叉链表中的空指针域存放指向该节点在某种遍历次序下的前驱和后继节点的指针（这种附加指针称为 “线索”）
2）这种加上了线索的二叉链表称为线索链表，相应的二叉树称为线索二叉树。根据线索性质的不同，线索二叉树可以分为前序线索二叉树、中序线索二叉树和后序线索二叉树三种。
3）一个节点的前一个节点称为前驱节点
4）一个节点的后一个节点称为后继节点

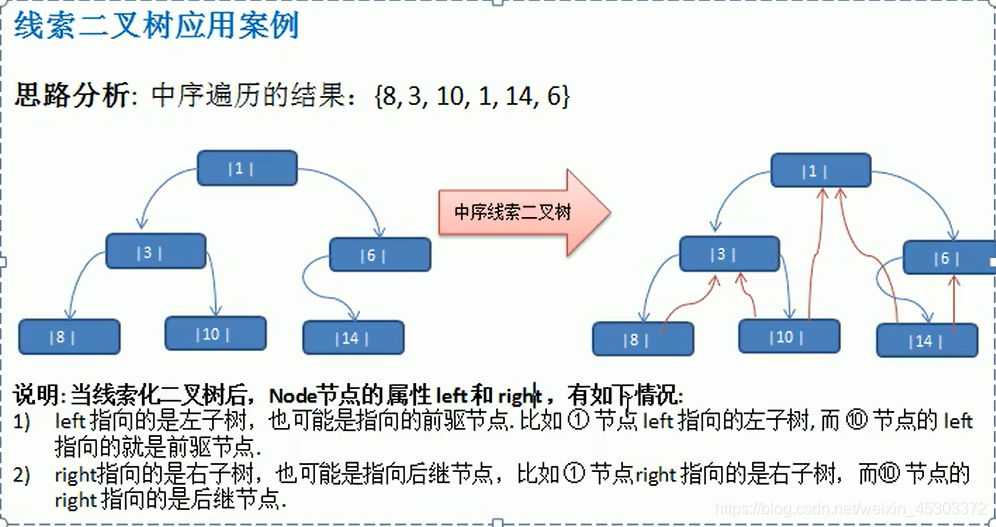
7.2 线索化二叉树的代码实现

//为便于线索化需要在HeroNode节点类中添加标志，并提供get、set方法
//说明
    //1.如果lefttype = 0 表示指向的是左子树，如果为 1 表示指向前驱节点
    //2.如果righttype = 0 表示指向的是右子树，如果为 1 表示指向后继节点
    private int lefttype;
    private int righttype;

	//在ThreadedBinaryTree中添加方法
	//为了实现线索化，需要创建要指向当前节点的前驱结点的指针
    //在递归进行线索化时，pre总是保留前一个节点
    private HeroNode pre = null;
    //对二叉树进行线索化的方法
    /**
     *
     * @param node 当前需要线索化的节点
     */
    public void threadedNodes(HeroNode node){
        //如果node == null ，不能线索化
        if (node == null){
            return;
        }

        //(1)线索化左子树
        threadedNodes(node.getLeft());
        //(2)线索化当前节点
        //处理当前节点的前驱节点
        if (node.getLeft() == null){
            //让当前节点的左指针指向前驱节点
            node.setLeft(pre);
            //修改当前结点的左指针类型
            node.setLefttype(1);
        }
        //处理后继节点
        if (pre != null && pre.getRight() == null){
            //让前驱节点的右指针指向当前节点
            pre.setRight(node);
            //修改前驱节点的右指针类型
            pre.setRighttype(1);
        }
        //每处理一个节点后让当前节点是下一个节点的前驱节点
        pre = node;

        //(3)线索化右子树
        threadedNodes(node.getRight());
    }

7.3 线索化二叉树的遍历

    //遍历线索化二叉树的方法
    public void threadedList(){
        //定义变量，存储当前遍历的节点，从root开始
        HeroNode node = root;
        while (node != null){
            //循环找到lefttype == 1的节点，第一个找到的就是8节点
            //后面随着遍历而变化，因为当lefttype==1是，说明该节点是按照线索化处理后的有效节点
            while (node.getLefttype() == 0){
                node = node.getLeft();
            }
            //打印当前节点
            System.out.println(node);
            //如果当前节点的右指针指向的是后继节点，就一直输出
            while (node.getRighttype() == 1){
                //获取当前节点的后继节点
                node = node.getRight();
                System.out.println(node);
            }
            //替换这个遍历的结点
            node = node.getRight();
        }
    }