后缀表达式是什么

后缀表达式也称逆波兰式（Reverse Polish notation，RPN，或逆波兰记法），也叫后缀表达式（将运算符写在操作数之后）。
若是没有学习过计算机知识可能一辈子都不会接触到这个表达式，我们日常生活中使用最频繁的是中缀表达式，例如1+1就是一个中缀表达式，其实就是操作符在俩操作数之间的表达式。
那么由中缀表达式就可以想象出后缀表达式，就是操作符在两个操作数之后。例如1+1的后缀表达式就是11+。

后缀表达式运算规则

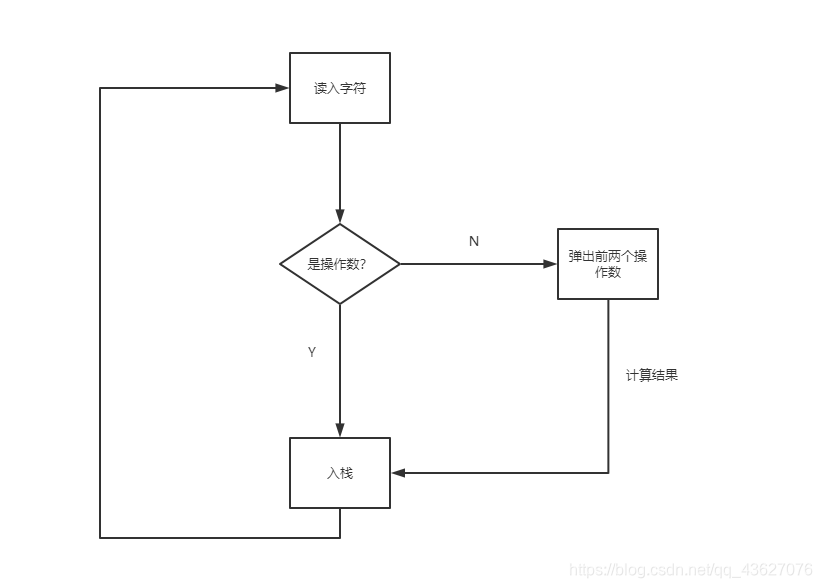
以栈计算后缀表达式为例
输入一个后缀表达式字符串之后，由左向右依次读取字符
1.读取到数字就直接入栈
2.当读入运算符就直接将栈中前两个数弹出，其中先弹出的为右操作数，后弹出的为左操作数，计算之后将结果压入栈中。
3.直至读取完毕，栈中剩余的数据的就是结果
一定是最终栈中只有一个数据，若是有多个数据则说明输入的后缀表达式有误。

为什么使用后缀表达式

对于我们来说自然是中缀表达式肯定是易懂并且易于计算，但是对于计算机来说可没有这么简单。
例如对于操作符之间的优先性，计算机可是很难判断先运算哪个操作符，但是后缀表达式就没有这个困难的地方。

流程图解

在这里插入图片描述

代码实现（c++）

重要代码

栈的数据结构

struct doubleStack
{
    double data[MAXSIZE];
    int top;
};

操作栈的方法

//初始化栈
void initStack(doubleStack &iStack)
{
    iStack.top=-1;
}
//入栈
void push(doubleStack &iStack,double a)
{
    if(iStack.top==MAXSIZE-1)
        throw 'm';
    iStack.data[++(iStack.top)]=a;
}
//获取栈顶元素
double top(doubleStack iStack)
{
    if(iStack.top==-1)
        throw 'w';
    return iStack.data[iStack.top];
}
//出栈
double pop(doubleStack &Stack)
{
    if(Stack.top==-1)
        throw 'w';
    Stack.top--;
    return Stack.data[Stack.top+1];
}

判断是否为操作符

bool isOp(char c)
{
    if(c!='+'&&c!='-'&&c!='*'&&c!='/'&&c!='('&&c!=')')
    {
        return false;
    }
    return true;
}

计算结果

double OpValue(char op,double a,double b)
{
    switch(op)
    {
    case '+':
        return a+b;
    case '/':
    {
        if(b==0)
            //除数为0异常
            throw '/';
        return a/b;
    }
    case '-':
        return a-b;
    case '*':
        return a*b;
    }

}

后缀表达式计算

//中缀表达式的计算
double Result(string a)
{
    doubleStack Stack;
    initStack(Stack);
    string::iterator it=a.begin();
    while(it!=a.end())
    {
        if(!isOp(*it))
        {
            push(Stack,(double)(*it-48));
        }
        else
        {
            if(Stack.top>=1)
            {
                double a=pop(Stack);
                double b=pop(Stack);
                double r=OpValue(*it,b,a);
                push(Stack,r);
            }
            else
            {
                //输入运算符之后但是栈内数据数量小于2 出现异常
                throw 'e';
            }
        }
        it++;
    }
    //最终剩余的站内数据大于一 出现异常
    if(Stack.top!=0)
        throw 'e';
    return top(Stack);
}

这里采用了抛出异常的方式，防止出现异常情况

主函数

int main()
{

    try
    {
        cout<<Result("11+23*-");
    }
    catch(char r)
    {
        switch(r)
        {
        //中缀表达式异常
        case 'e':
            cout<<"There is a problem with infix expression";
            break;
        //除数为0异常
        case '/':
            cout<<"An exception with a divisor of 0";
            break;
        case 'm':
            //栈满了
            cout<<"Stack with abnormal";
            break;

        case 'w':
            //栈空
            cout<<"Empty stack anomalies";
            break;

        }
    }
}

用惯了java，感觉还是异常捕获比较好用