[数据结构与算法] Tree2——遍历变种之自顶向下

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> Tree2——遍历变种之自顶向下 -> 正文阅读

[数据结构与算法]Tree2——遍历变种之自顶向下

树的基础遍历包括前序、中序、后序和层序，遍历方法大致可以分成使用 DFS 或 BFS。除了基础遍历外，还要很多其他的变体，总体可以分成两类：自顶向下 或 非自顶向下。

这篇主要记载一些自顶向下的遍历问题。

1. 二叉树的最大深度

题目链接：104. 二叉树的最大深度
题目描述：给定一个二叉树，找出其最大深度。二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。 (叶子节点是指没有子节点的节点)

1.1 DFS-递归解法

思路

因为要求的是二叉树的深度，很自然的会从深度优先搜索的角度思考，如果已知根节点的左子树和右子树的深度分别为 left_height、right_height，那么该二叉树的最大深度即
$max(left{\_}height,\ right{\_}height)\ +\ 1$
而左子树和右子树的深度又能够以同样的方式进行计算，显然这一过程具有递归性质，因此我们可以利用递归计算二叉树的最大深度。

算法流程

对当前二叉树的最大深度：
- 递归计算左子树的最大深度；
- 递归计算右子树的最大深度；
利用上述公式只需在 $O (1)$ 时间内计算出当前二叉树的最大深度；
递归终止的条件为遇到空节点，此时返回值为0。

参考代码

def maxDepth(root):
    if not root:
        return 0
    else:
        left_height = maxDepth(root.left)  # 自身调用递归计算左子树的深度
        right_height = maxDepth(root.right)  # 自身调用计算右子树的深度
        return max(left_height, right_height) + 1

算法性能

时间复杂度： $O (n)$ ，其中 $n$ 是二叉树的节点数，因为每个节点在递归中被遍历一次且只有一次。
空间复杂度： $O (d e p t h)$ ，其中 $d e p t h$ 为二叉树的深度。因为递归过程需要隐式维护一个栈，栈的空间消耗又取决于递归的深度(即二叉树的深度)，因此空间复杂度本质上取决于二叉树的深度。

1.2 BFS-队列辅助解法

思路

如果从广度优先搜索的角度来看，这个问题的思路也很清晰：我们只需要维护一个变量 depth 表示遍历过的层，每遍历一层令 depth + 1，那么当所有层都遍历完后，二叉树的深度即 depth。这与层序遍历的思想几乎一致。

算法流程

初始化队列为根节点；
在遍历当前层时，我们需要将该层每个节点的子节点都添加到队列中，以保证遍历完之后的队列中存储了下一层的所有节点，因此需要记录当前队列的长度 cur_size；
每遍历一个节点时，应判断其是否存在左右节点，若存在则入队，同时令 cur_sze - 1，直至为 0，就表示当前层的节点已全部遍历完了，所以再令 depth + 1。
当队列为空时，遍历结束，depth 即二叉树的深度。

参考代码

def maxDepth(root):
    if not root:  # 根节点为空时深度为0
        return 0  
    
    depth = 0
    queue = [root,]
    
    while queue:
        cur_size = len(queue)    # 记录当前队列长度
        while cur_size > 0:      # 当前队列不空前一直进行遍历
            root = queue.pop(0)  # 弹出队首节点
            if root.left:        # 判断左子树是否存在
                queue.append(root.left)
            if root.right:       # 判断右子树是否存在
                queue.append(root.right)
            cur_size -= 1        # 遍历完一个节点，当前队列长度-1
        depth += 1               # 遍历外当前队列，层数+1，即深度+1

   return depth

算法性能

时间复杂度： $O (n)$ ，其中 $n$ 为二叉树的节点个数，每个节点只会被访问一次。
空间复杂度： $O (n)$ ，空间的消耗取决于队列存储的元素数量，其在最坏情况下会达到 $O (n)$ 。

1.3 层序遍历+len()

思路

这是个投机取巧的办法哈哈哈~
我们知道二叉树的层序遍历会按照一层一层的返回一个二维数组，其中一个子列表存储了一个层的所有节点，也就是说层序遍历输出列表的长度即二叉树的层数。

因此，如果在已经进行了层序遍历的情况下，可以通过对层序遍历的结果使用方法 len() 计算长度，该长度即二叉树的最大深度。

参考代码

def maxDepth(root):
    # 利用层序返回其长度
    if not root:
        return 0
        
    res, queue = [], [root,]

    while queue:
        n = len(queue)
        level = []
        for i in range(n):
            root = queue.pop(0)
            if root:
                level.append(root.val)
                if root.left:
                    queue.append(root.left)
                if root.right:
                    queue.append(root.right)
        res.append(level)
    return len(res)

2. 路径总和

题目链接：112. 路径总和
题目描述：给定二叉树的根节点 root 和一个表示目标和的整数 targetSum ，判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。

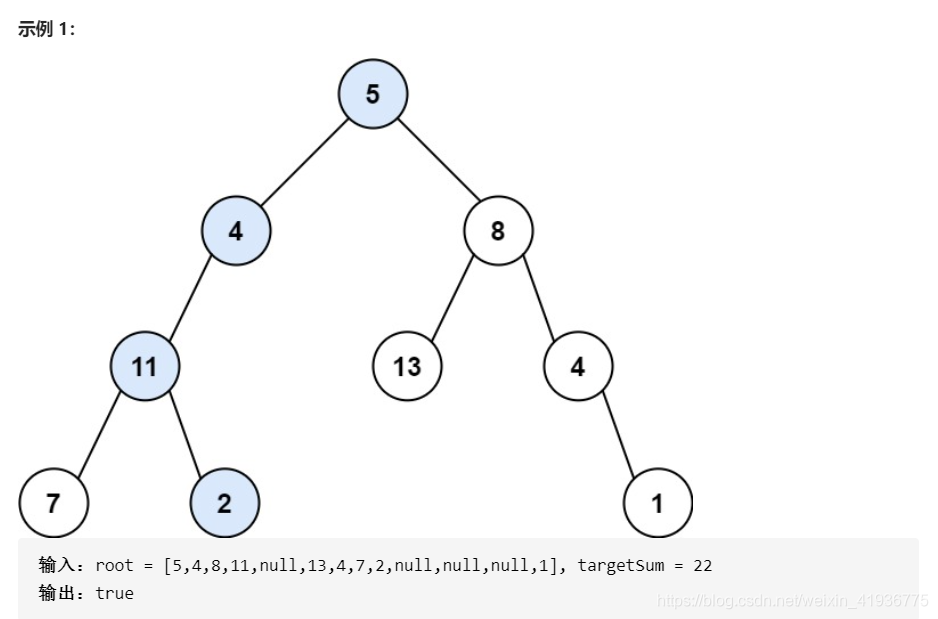
2.1 DFS-递归解法

思路

原问题：判断树 root 中是否存在一条从 根节点到叶子节点 的路径满足路径之和等于 targetSum。
<==>：判断是否存在一条从 根节点的子节点到叶子节点 的路径满足路径之和等于 targetSum - root.val。
<==>：判断是否存在一条从 当前节点的子节点到叶子节点 的路径满足路径之和等于 targetSum -Val，其中 Val 表示从根节点到当前节点的路径之和。
很显然，上述过程满足递归的性质。

算法流程

对于根节点为空的情况，返回 False；
对于根节点无子节点的情况，只需判断 targetSum == root.val；
对于一般情况：递归判断其子节点是否满足条件。

参考代码

def hasPathSum(root, targetSum):
    if not root:
        return False
    if (not root.left) and (not root.right):
        return targetSum == root.val
    return hasPathSum(root.left.val, targetSum-root.val) or hasPathSum(root.right.val, targetSum-root.val)

算法性能

时间复杂度： $O (n)$
空间复杂度： $O (h e i g h t)$ ，其中 height 为树的高度，主要取决于递归过程中栈的开销，平均情况下树的高度与节点数的对数正相关，空间复杂度为 $O(log\ n)$ ，最坏情况下树呈链状，此时空间复杂度为 $O (n)$ 。

2.2 BFS-双队列解法

思路
题目要求的输出既涉及到节点(根节点到叶子节点)，也涉及到节点值(路径之和)，如果使用广度优先搜索，那么我们需要 创建两个队列，分别存放将要遍历的节点和根节点到这些节点的路径和。

算法流程

参考代码

def hasPathSum(root, targetSum):
    if not root:
        return False
        
    que_node = [root,]
    que_val = [root.val,]
    
    while que_node:
        now = que_node.pop(0)
        temp = que_val.pop(0)
        if (not now.left) and (not now.right):
            if temp == targetSum:
                return True
            continue
        if now.left:
            que_node.append(now.left)
            que_val.append(now.left.val + temp)
        if now.right:
            que_node.append(now.right)
            que_val.append(now.right.val + temp)
    return False

算法性能

时间复杂度： $O (n)$ 。
空间复杂度： $O (n)$ ，主要取决于队列的空间消耗，队列中的元素不会超过树的节点数。

3. 路径总和 II

题目链接：113. 路径总和 II
题目描述：给出一个二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。叶子节点 是指没有子节点的节点。

3.1 DFS+递归

思路

根据题目要求，我们需要对树进行遍历，在遍历的同时记录从根节点到当前节点的路径和，以防止重复计算。同时由于要找出所有满足条件的路径，就需要枚举每一条从根节点到叶子节点的路径，当遍历到叶子节点并且此时路径和恰为目标值时，就找到了一条满足条件的路径。显然可以使用 DFS 来遍历节点。

算法流程

首先判断当前节点 root 是否存在；
若存在，记录节点值 root.val，并更新目标值 target -= root.val；
判断当前节点是否是叶子节点与路径和是否满足条件：
- 若满足，则将当前路径加入答案列表；
- 否则，只需递归寻找当前节点的左、右子节点到叶子节点且满足路径和为 target 的路径。

参考代码

class Solution:
    def pathSum(self, root: TreeNode, targetSum: int) -> List[List[int]]:

        DFS
        res = []
        path = []

        def dfs(root, targetSum):
            if not root:
                return
            
            path.append(root.val)
            targetSum -= root.val
            if not root.left and not root.right and targetSum == 0:
                res.append(path[:])
            dfs(root.left, targetSum)
            dfs(root.right, targetSum)
            path.pop()

        dfs(root,targetSum)
        return res

算法性能

时间复杂度： $O(n^2)$ ，其中 $n$ 是树的节点数。在最坏情况下，树的上半部分为链状，下半部分为完全二叉树且从根节点到叶子节点的每一条路径都满足条件，此时路径数为 $O (n)$ ，每条路径上的节点数也为 $O (n)$ 。
空间复杂度： $O (n)$ ，取决于递归过程中隐式栈的开销，最大不会超过树的节点数。

3.2 BFS+哈希表+双队列

（该方法没有太看懂😔😕）

思路

我们也可以采用广度优先搜索的方式，遍历这棵树。当我们遍历到叶子节点，且此时路径和恰为目标和时，我们就找到了一条满足条件的路径。

为了节省空间，我们使用哈希表记录树中的每一个节点的父节点。每次找到一个满足条件的节点，我们就从该节点出发不断向父节点迭代，即可还原出从根节点到当前节点的路径。

参考代码

class Solution:
    def pathSum(self, root: TreeNode, targetSum: int) -> List[List[int]]:

        ret = list()
        parent = collections.defaultdict(lambda: None)

        def getPath(node: TreeNode):
            tmp = list()
            while node:
                tmp.append(node.val)
                node = parent[node]
            ret.append(tmp[::-1])

        if not root:
            return ret
        
        que_node = collections.deque([root])
        que_total = collections.deque([0])

        while que_node:
            node = que_node.popleft()
            rec = que_total.popleft() + node.val

            if not node.left and not node.right:
                if rec == targetSum:
                    getPath(node)
            else:
                if node.left:
                    parent[node.left] = node
                    que_node.append(node.left)
                    que_total.append(rec)
                if node.right:
                    parent[node.right] = node
                    que_node.append(node.right)
                    que_total.append(rec)

        return ret