给你一个 n x n 的二进制矩阵 grid 中,返回矩阵中最短 畅通路径 的长度。如果不存在这样的路径,返回 -1 。
二进制矩阵中的 畅通路径 是一条从 左上角 单元格(即,(0, 0))到 右下角 单元格(即,(n - 1, n - 1))的路径,该路径同时满足下述要求:
1、路径途经的所有单元格都的值都是 0 。
2、路径中所有相邻的单元格应当在 8 个方向之一 上连通(即,相邻两单元之间彼此不同且共享一条边或者一个角)。
畅通路径的长度 是该路径途经的单元格总数。
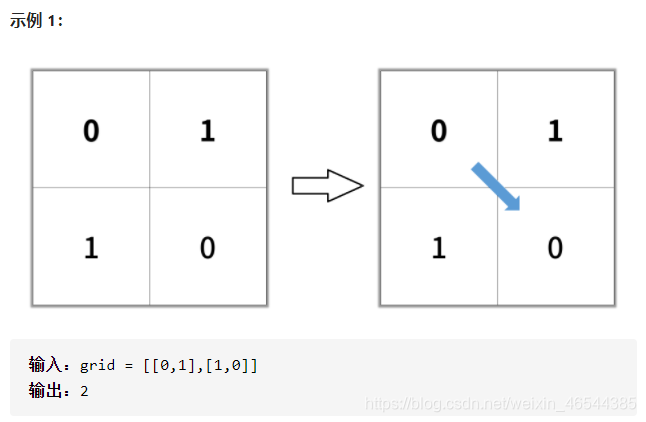

提示:
n == grid.length
n == grid[ i ].length
1 <= n <= 100
grid[ i ][ j ] 为 0 或 1
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/shortest-path-in-binary-matrix
起初想着利用深度优先搜索来实现的,但是当提交代码的时候,发现会超时,因为每一个位置都需要往8个方向进行深度优先搜索,并且在下面的提示有说到n的范围,那么就会有n * n个位置需要进行深度优先搜索。时间复杂度
O(8 ^(n*n)),可见极其容易发生超时。(时间复杂度可能说错了,如果有大佬清楚的话,请指教哈)
利用深度优先搜索的代码:
class Solution {
int result = Integer.MAX_VALUE;
/*
利用深度优先搜素的时候会超时
*/
public int shortestPathBinaryMatrix(int[][] grid) {
if(grid == null || grid.length == 0 || grid[0].length == 0)
return -1;
int col,row;
col = grid.length;
row = grid[0].length;
if(grid[0][0] == 1 || grid[col - 1][row - 1] == 1)
return -1;//如果起点或者终点有一个是1,说明不能构成路径,直接返回-1
dfs(grid,0,0,col,row,1);//当在(0,0)这个位置的时候已经走了1步,所以step起初是1
if(result == Integer.MAX_VALUE)
return -1;
return result;
}
public void dfs(int[][] grid,int x,int y,int col,int row,int step){
if(x < 0 || x >= col || y < 0 || y >= row || grid[x][y] == 1){
return;
}
if(x == col - 1 && y == row - 1){
result = Math.min(result,step);
return;
}
grid[x][y] = 1; //如果当前位置为0,那么将其置1,表示已经访问过了,然后进入递归,访问它的8个方向的位置
dfs(grid,x + 1,y,col,row,step + 1);//下
dfs(grid,x,y + 1,col,row,step + 1);//右
dfs(grid,x,y - 1,col,row,step + 1);//左
dfs(grid,x - 1,y,col,row,step + 1);//上
dfs(grid,x + 1,y + 1,col,row,step + 1);//右下
dfs(grid,x - 1,y + 1,col,row,step + 1);//右上
dfs(grid,x + 1,y - 1,col,row,step + 1);//左下
dfs(grid,x - 1,y - 1,col,row,step + 1);//左上
/*
将8个方向都访问过之后,需要将其恢复,如果不恢复的话,那么会导致最后
结果错误
*/
grid[x][y] = 0;
}
}
运行结果:
所以,本题利用的是广度优先搜索来解决.基本过程:
1、定义一个队列,其中这个队列的泛型是一个一维数组,用于存放当前需要所在的位置,所以存放到队列中的一维数组是一个长度为2的数组,并且下标为0的数对应的是行下标,下标为1的数对应的是列下标。
2、将起点压入到队列中,并且需要将起点标记已经访问过了,即将对应的值值为1。不要忘了这一步,每次将一个位置压入到队列的时候,需要将这个位置对应的值置为1,标记已经走过了,那么下次就不会在将这个位置压入到队列中了.
3、获取当前队列的元素个数size = queue.size().表示第step步中一共有size个位置可以选择。
4、将队列中的size个位置跳出,然后将对应的8个方向的可以移动的位置压入到队列中,从而作为第step + 1步的选择。
5、当size个位置都已经遍历完之后,step ++,否则,如果size个位置中如果有一个位置是终点,那么就可以直接返回step。之所以可以直接返回,是因为题目要求的是最短路径。
6、否则如果将会所有的队列遍历完时,都没有返回结果,说明没有办法得到路径,所以直接返回-1.
如果还不太理解,请看一下下面的图解:
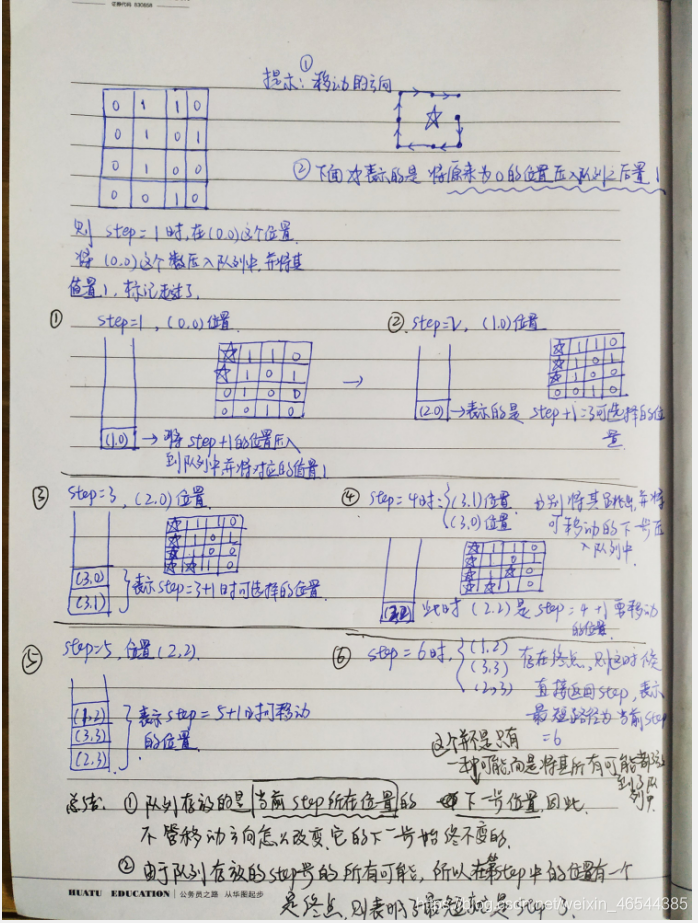
对应的代码:
class Solution {
/*
通过定义长度为8的数组,表示当前位置的下一步可能位置
*/
int[] move_x = new int[]{0,1,1,1,0,-1,-1,-1};
int[] move_y = new int[]{1,1,0,-1,-1,-1,0,1};
public int shortestPathBinaryMatrix(int[][] grid) {
if(grid == null || grid.length == 0 || grid[0].length == 0)
return -1;
int col,row,x,y,i,j,a,b;
int size,step = 1;//表示从起点走到终点要走多少步
col = grid.length;
row = grid[0].length;
if(grid[0][0] == 1 || grid[col - 1][row - 1] == 1) //如果终点或者起点中有一个位1,说明不能构成路径,直接返回-1
return -1;
Queue<int[]> queue = new LinkedList<int[]>();//泛型是一个数组,并且这个数组是长度为2,表示这个数的行下标、列下标
queue.offer(new int[]{0,0});
grid[0][0] = 1;//注意起点不要忘记这一步,标记起点已经访问过了
while(!queue.isEmpty()){
size = queue.size();//之所以要将队列中的size个跳出队列,因为这size个对应的就是第step步的位置
for(j = 0; j < size; j++){
int[] arr = queue.poll();
x = arr[0];
y = arr[1];
if(x == col - 1 && y == row - 1){
//如果在第step中有可能移动到终点,那么直接返回step
return step;
}
for(i = 0; i < 8; i++){
a = x + move_x[i];
b = y + move_y[i];
//如果当前位置的下一步位置发生了越界,或者已经走过了,那么直接进入下一次循环
if(a < 0 || a >= col || b < 0 || b >= row || grid[a][b] == 1)
continue;
queue.offer(new int[]{a,b});
/*
标记已经访问过了(这一步是必须的,如果没有这一步,那么就会导致有一些已经访问过
的位置再次压入到队列中
*/
grid[a][b] = 1;
}
}
step++;
}
return -1;
}
}
运行结果:
