图
图的基本概念与运算




总的来说就是一堆结点,还有连接他们的边(边可以是单向的或双向的,边上可以有权重也可以没有),边是否有向决定是有向图还是无向图,边上是否有权重决定是否是网络。
路径与回路

连通图
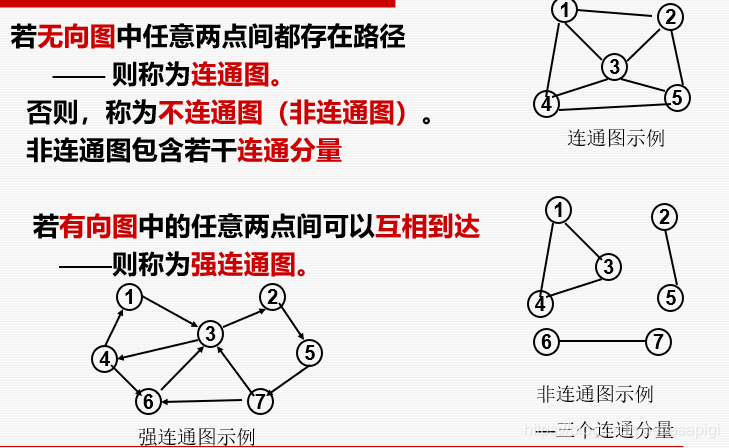
完全图
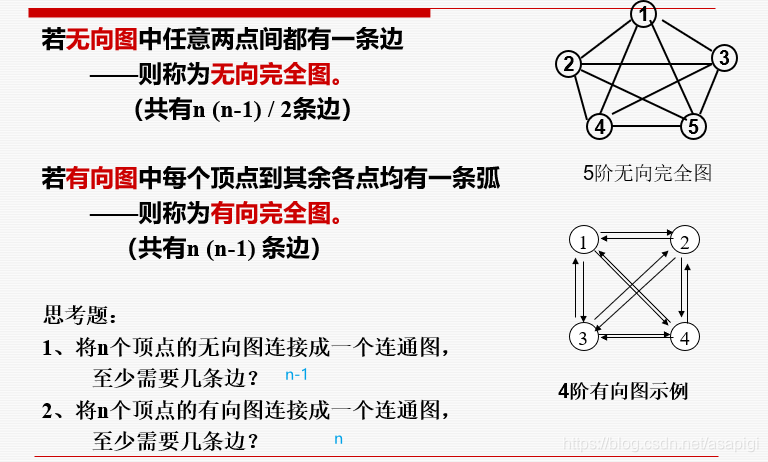
树与有向树
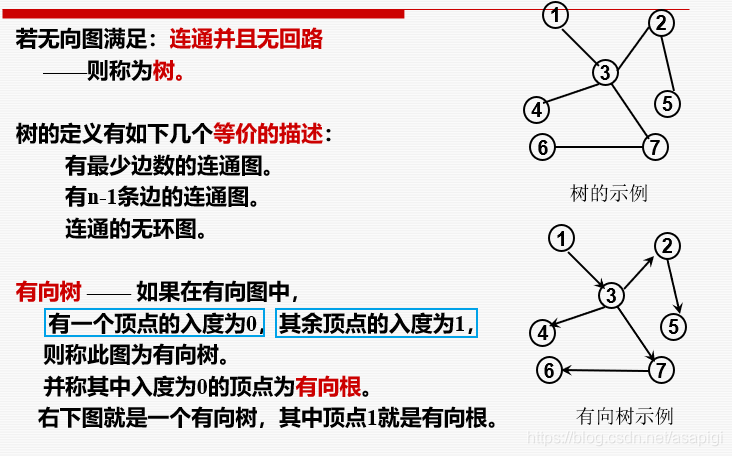
图的运算


图的存储
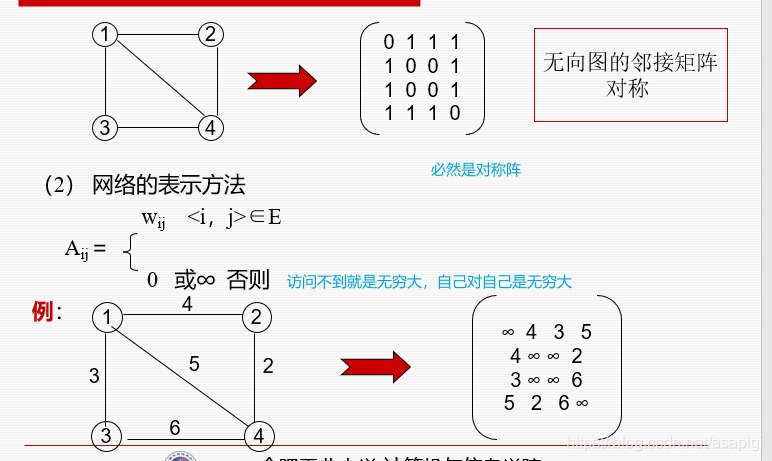
邻接矩阵
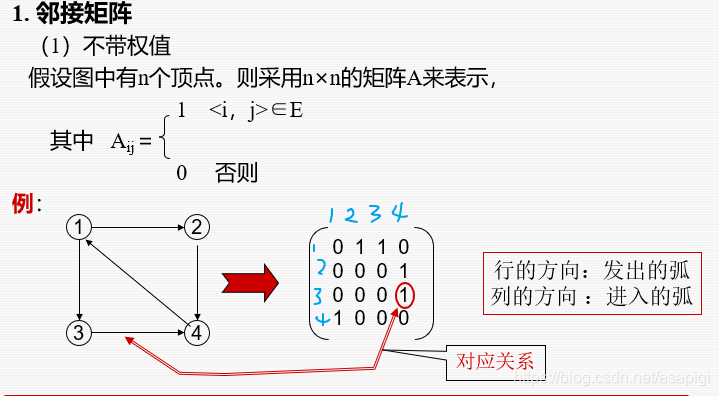
从行看,该行上有1说明该行对应的结点能访问到1所在的列对应的结点
,所以从列看的话就是能访问到该列的行。那么我们从两个角度出发都能表示所有的边关系,1.每个结点都能访问到那些结点2.每个点都能被那些结点访问。即只看行或只看列。
邻接表
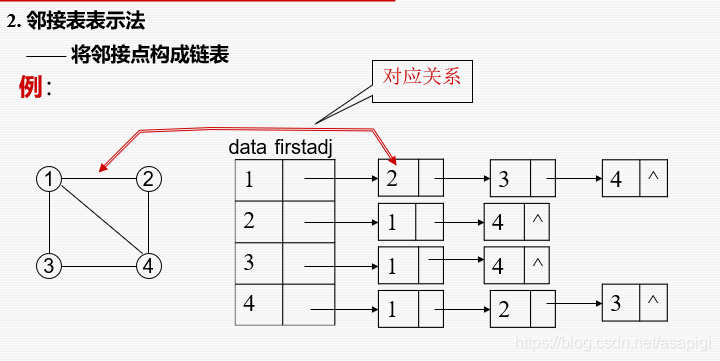
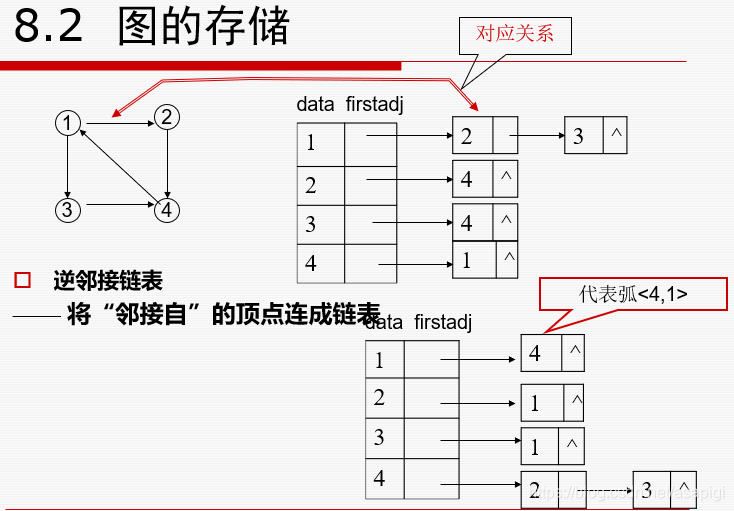
与邻接矩阵相比的优点:1.找能访问到哪些点比较方便不用像邻接矩阵那样遍历一行
缺点:找能被那些结点访问很麻烦要全部遍历一遍
图的遍历

深度优先遍历
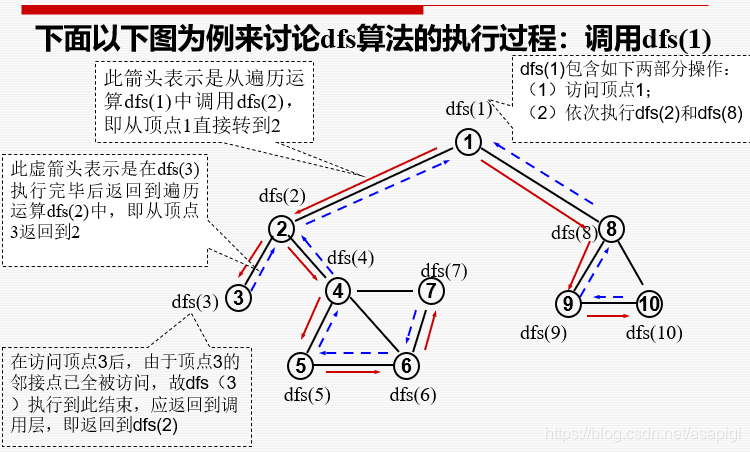
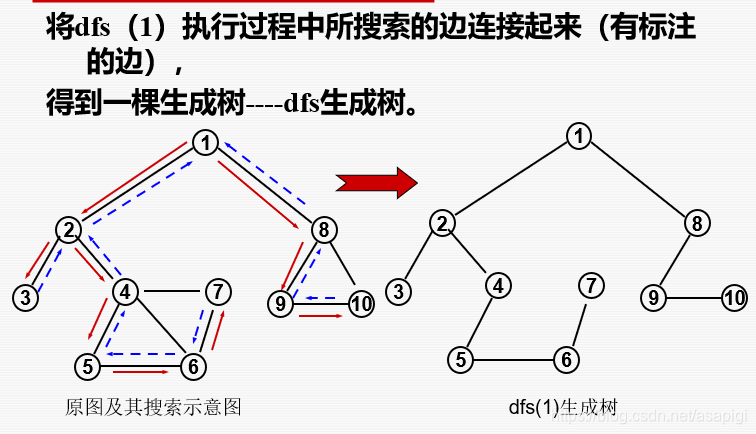


visit中0表示还没被访问过1表示已被访问过。
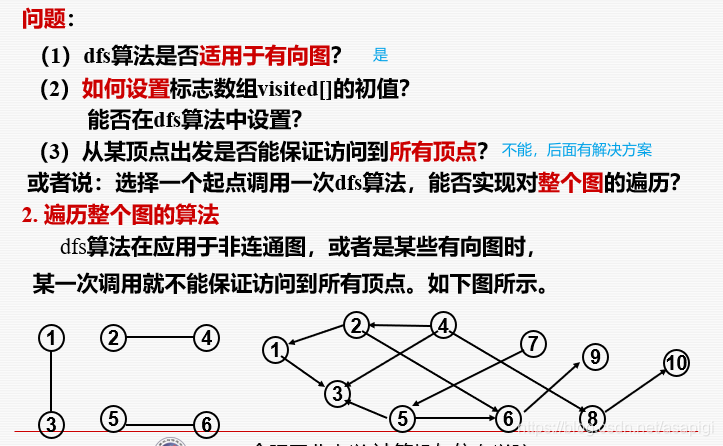

解决无法访问到所有点的问题
拓展

例题




E除以2是因为无向图是双向连通的
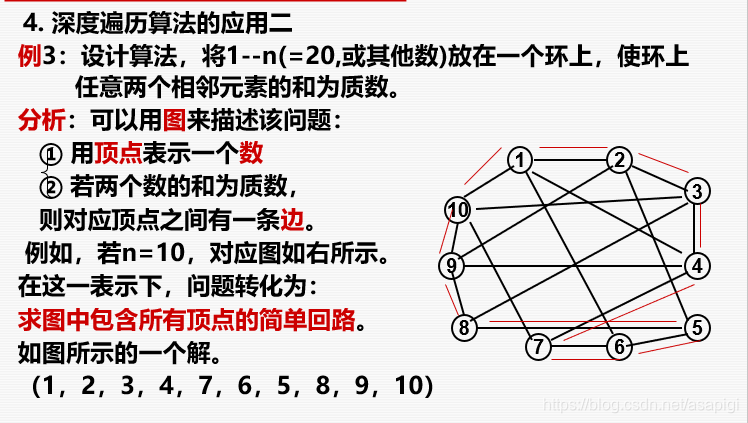


就是从一个点开始不断尝试地把周围的相邻点放入(一次尝试放一个,不行就退回去拿另一个),并记录在路径中,并记录路径的长度,一旦路径长度达到要求并且满足首尾相连就打印,否则就往回退,其中到终点时不满足首尾相连时要退两步(因为退一步最后那个节点还是同一个),但下面的代码并不是完全按照这个思路敲的(4里的两个要求被很好得解决了,不用分类)


第一句是放入该节点的尝试,第二句是不放入该节点的尝试,那么这个程序的运行过程差不多是这样的:先一条路线走到黑,不行就往回退,完全相同的路不会被走两次,这就保证了(4)里面的两条要求。
广度优先遍历

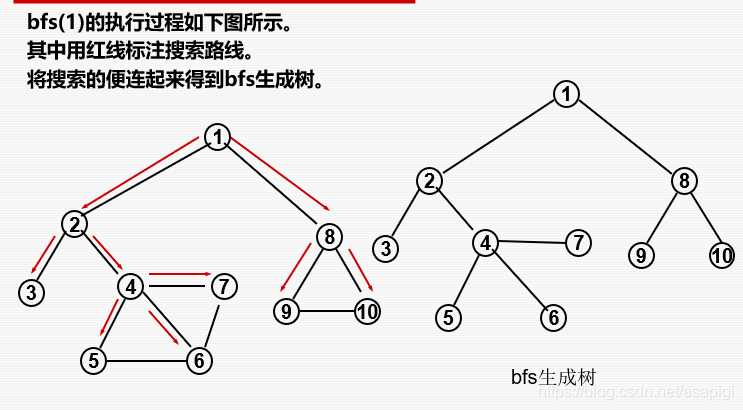



两者的区别
在树上比较能看出广度与深度优先的区别。
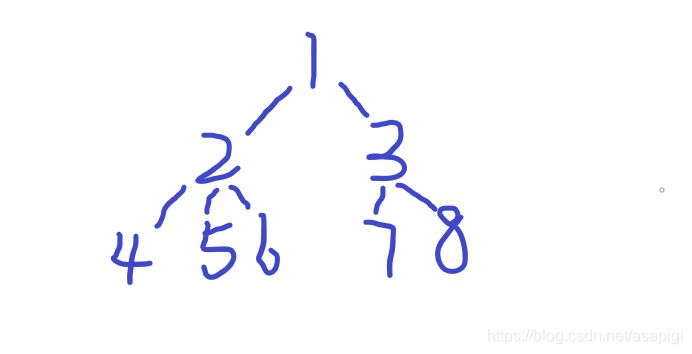
以这棵树为例,深度优先先访问当前节点然后会不断地以相同的方式访问它的孩子,而广度优先则是不断访问目前结点的所有结点,全部访问完后再依次让其孩子重复此操作(不访问自己,所以需要我们提前访问根节点)。
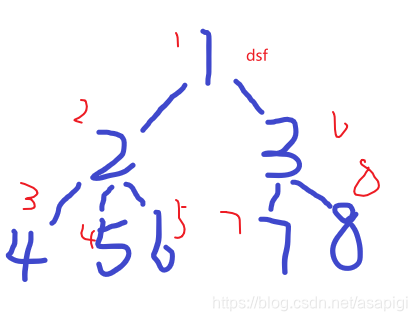
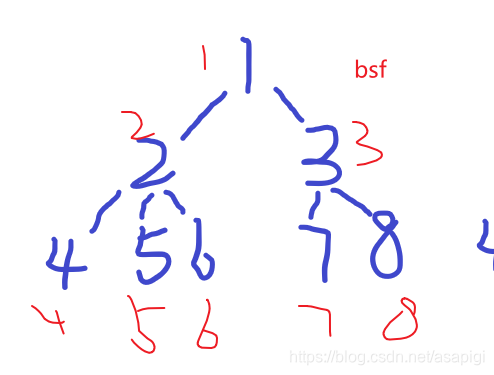
一个不断往深处走到底后返回并继续往深处走,另一个一层一层走。
就像是走迷宫,一个是一条路走到黑,发现不通了才退回来,另一个是先把当前已知的路都先走一点,没找到出口就再把目前已知的路往前再走一点。
最小生成树
问题引入

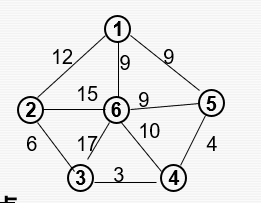
prime算法

就是说随便挑一个点,然后我们搞一个候选边集合,如果某条边的一端被选中,那么他就应该被放到集合中,每次从候选边中拿出(拿出来后就不在集合中了)权重最小的边,然后选中它的另一端的结点,这个结点被选中后会带来一堆新的候选边,继续下去直到所有结点被选中。
以上面的图为例:
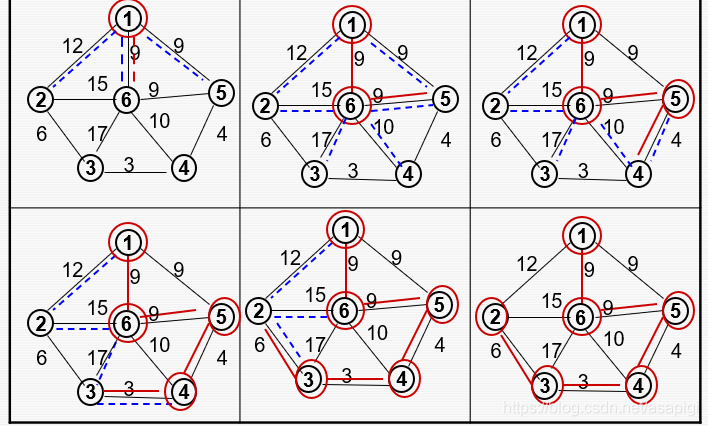
红圈表示被选中的结点,蓝线表示侯选边,红线表示被拿出侯选边集合的边。
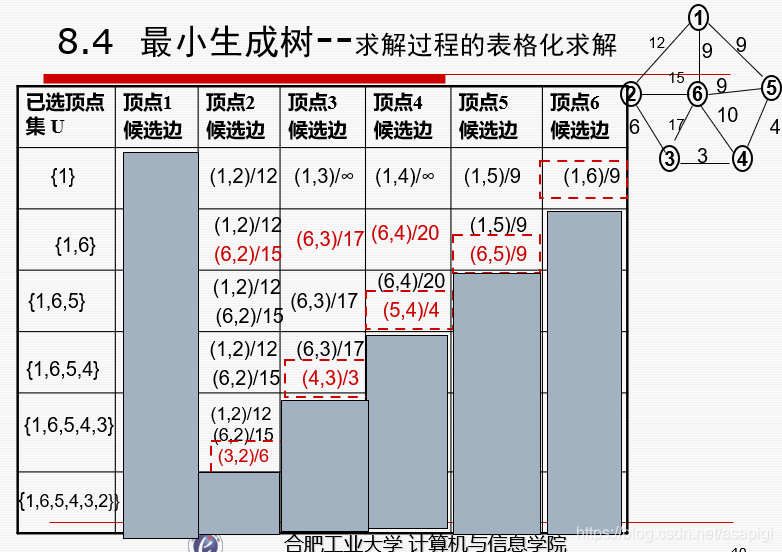
算法实现


错了,prim算法的时间复杂度就是O(n*n)

一点一点来看:

第一个是我们原来的图,里面存有结点与边的信息,T是要输出的图(最小生成树)

将select数组全部置否,然后随便挑一个作为起点,将其对应的位置置True(select是用来保存结点是否被选中的数组)

之前说把边塞到集合中,但这里没有这么做,先看一下edges是个啥,这是一个结构体数组,这个结构体有两个成员,一是vj,意思是从哪来,二是w意思是边上的值,而结构体数组的下标表示这个未被选中的结点的编号,这样就有了边的信息;然后是A,A是G的邻接矩阵;最后看一下代码的意思,意思是说遍历所有结点,如果能被v0访问到就将vj设为v0,w设为边上的值,如果访问不到就只将w设为∞(看起来多此一举,但是后面的代码要遍历这个edge数组,而我们事先没有赋值,那访问未初始化的内容总不太好),这样的话,我们找最小的侯选边只要遍历这个数组就行了,而且另一端的点也一起准备好了。
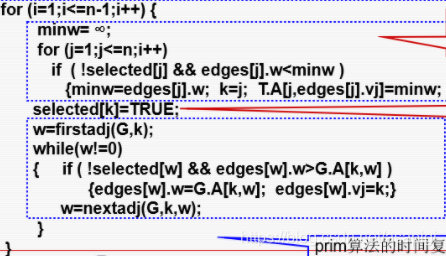
这个最大的循环里面的代码每运行一次就会选中一个点,之前有一个了,所以再来n-1个就行了。

这个for是遍历edges数组找出最小的边并将边和结点的信息跟新到T中将节点设置为选中(感觉把第三句放外面跟好一点),注意只有另一端是未选中的点的边才能参与

由于一个新的点被选中,侯选边增加了,所以要更新edges数组的信息,就是把新结点能访问到的没有被访问过结点对应的边与与该结点存在edges中的最小边进行对比,如果比原来的小就更新。
kruskal算法

那怎么判断是否形成回路

由于每个结点的初始电位不同,连在一起的结点的电位是一样的,所以只要判断新添加一条边时两端的电位是不是一样的就行了。


有向无环图
问题引入

AOV
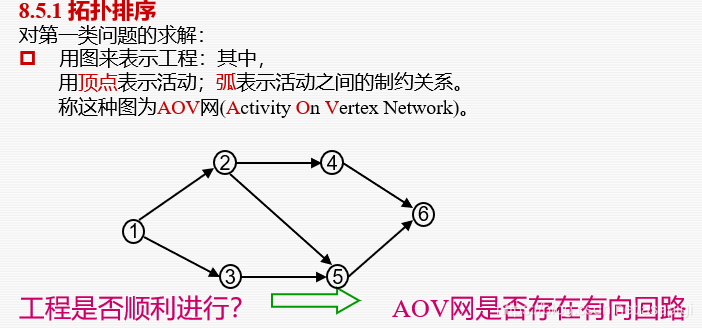



变成橙色表示这个点,边消失


右边的格子是各节点的入度情况,下面是放入度为0的结点的栈,每次出栈都会导致其他结点入读的变化。
代码实现

就是先遍历一遍所有结点,把入度为零的结点入栈,然后不断出栈,每出一个就把他能访问到的结点的入度减一(在这个过程中如果出现入读为0的要赶紧入栈)直到栈为空,最后比较答应出来的序列的结点个数与n是否相等来判断是否有拓扑序列
习题
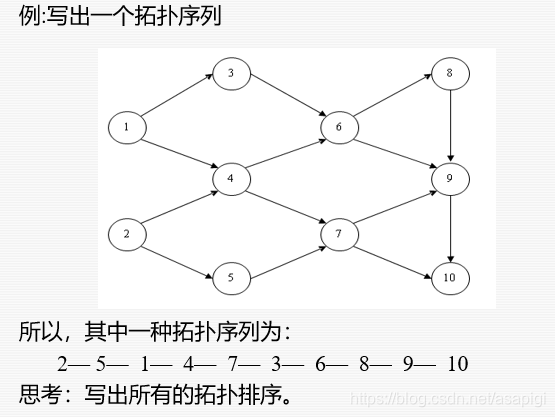
提示:可以以某个结点为分割点做一个分类,分类的依据是该节点前面的结点(指拓扑序列)不考虑顺序,就是说只要某个结点前面的结点一样那么这个结点后面的序列就会一模一样,这个规律自己画几条拓扑序列就很容易看出来。
AOE
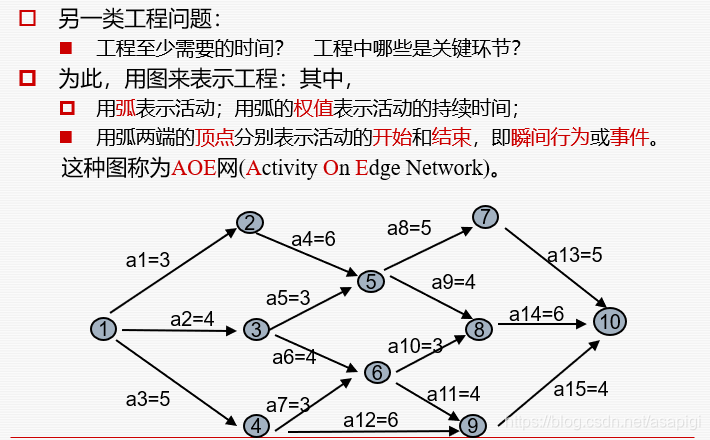
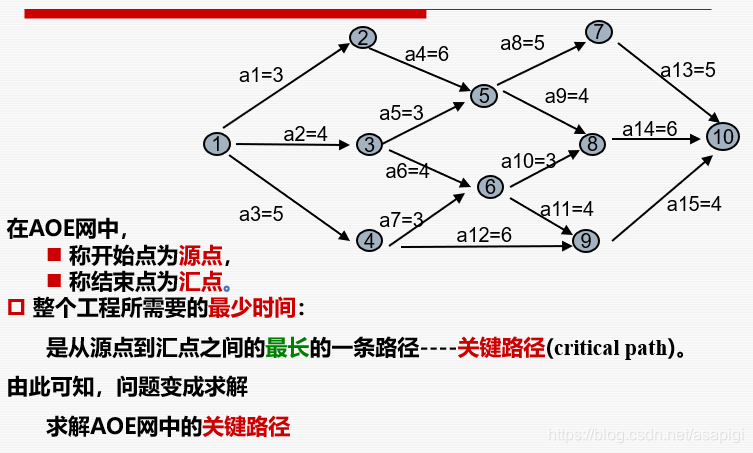
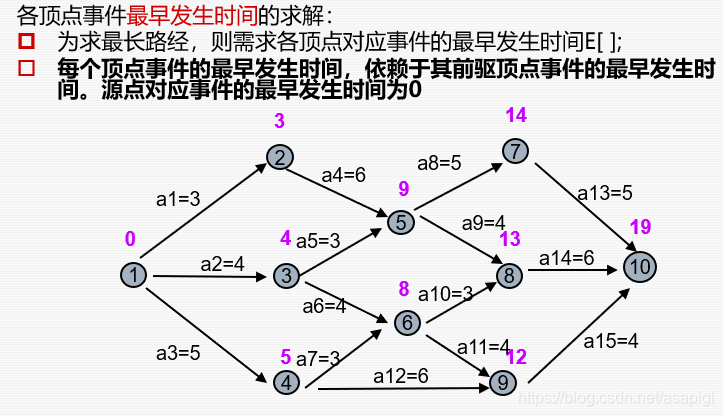

刚开始时将E中所有元素置零,然后我们在前面拓扑序列代码上进行如下更改:在一个点出栈时要遍历他能访问到的点,在遍历的过程中添加
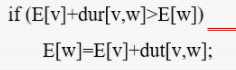
这样就产生了一个效果:每个节点的E上面的值是由能访问到他的结点的最大值决定的,就是
这句话的含义,解释一下为什么要最大值,是这样的,如果我们选小的,那么当小的那个完工后我们做这个结点的工作,但是问题是大的那个没完成我们做不了这个结点的工作,所以要选大的。
还有一个问题,最短完工时间存在哪:最后一个节点
接下来是关键路径的求解
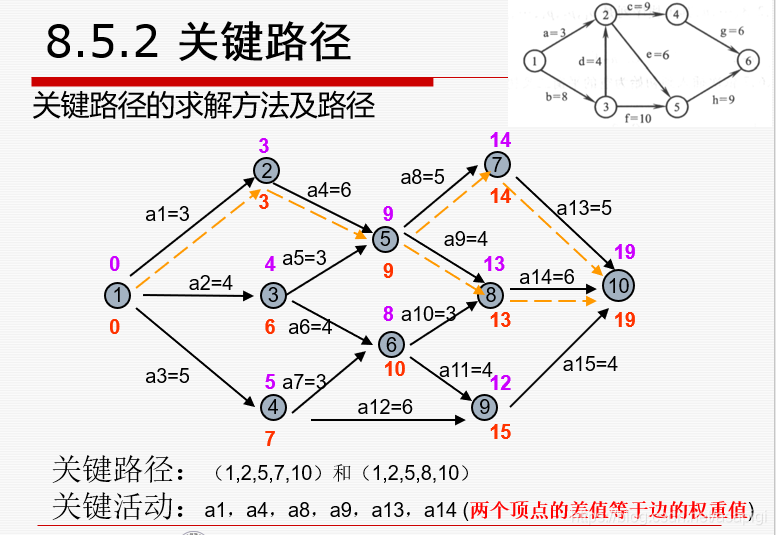
这个的话,还记得前面那个选最大值吗,就是要找出那些边,那是决定工期的关键路径,然后这里要从后往前(因为从前往后还得不断疯狂试探,如果想不开可以试试),由于关键路径是那些最大值组成的,它区别于其他结点的特征是边上的权重与两个点的差一样(因为就是从他过来的)
练习
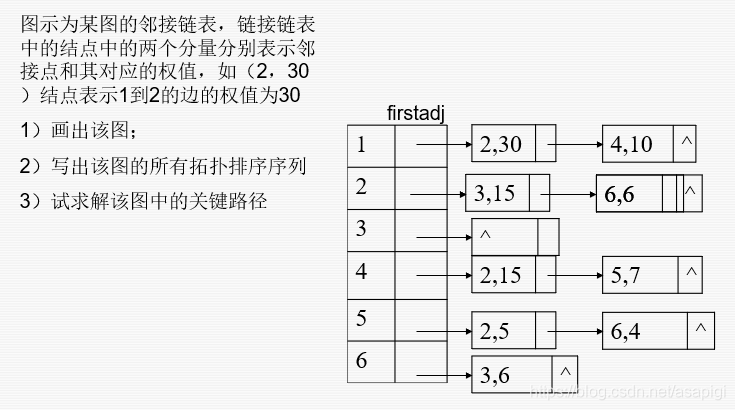
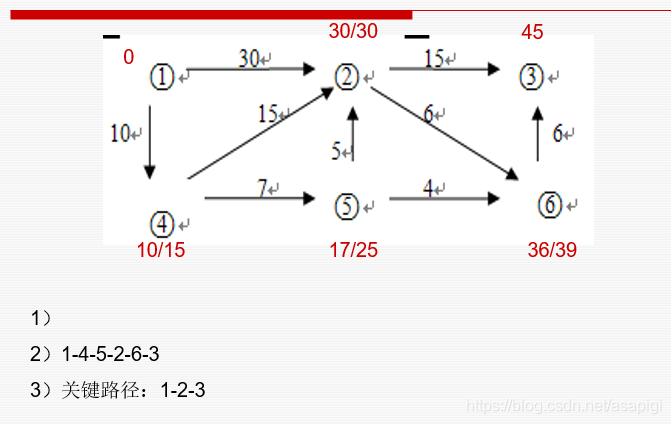
最短路径

Dijkstra算法
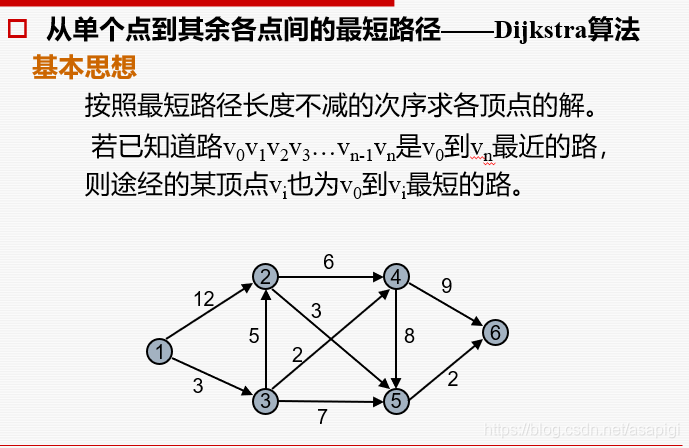
就是说我要从A到C,然后经过了B,那么A到B,B到C的距离都是最短的,很好理解,如果不是最短,那就换那条路这样总的路程减少了这与最短路径矛盾。
利用这个结论我们求一个点到另一个点的距离可以转化为不断求中间点的距离,不断更新最短距离(就是每次新并入一个点就更新到某个点的最短距离,等到该点周围的边都被覆盖了,留下来的距离就是最短距离)。

来个动图感受一下

代码

代码比较好懂,不说了。
Floyd算法

A们是nxn的矩阵
A(k)[i,j]表示从结点i到结点j的最短路径但是要求该路径经过的结点的编号不能大于k。
那么A(n)就是一个记录了从某个点到其他点的最短距离的矩阵。那么其他A存在的意义是什么呢?
A(k-1)用是用来求A(k)[i,j]的。具体怎么搞。看下图
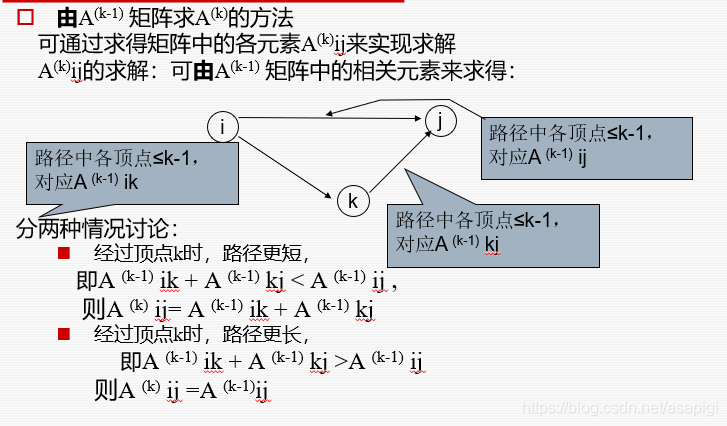

这里有个点就是A(k)的第k行和第k列直接抄上一个的,因为从自己出发,中间根本不会经过自己,所以只有一种情况,直接抄。
代码实现

这个虽然原理有一点绕,但是代码还是很简单的。