本文总结了计算机专业保研面试中较为常考的算法题目,也是博主当年的备考材料。如果这篇文章对你有帮助,请给博主点个赞鼓励一下吧。
- 排序算法
- 综述

- 评价标准
- 时间复杂度:比较+移动/交换,最好/最坏/平均
- 空间复杂度:是否原地排序
- 稳定性:顺序的问题
- 常见算法
- 插入排序(稳定)
- 通过while向前移动

-

- 最好:O(n);最坏:O(n^2).
- 通过while向前移动
- 选择排序(不稳定)
- 每次选择最小的元素交换
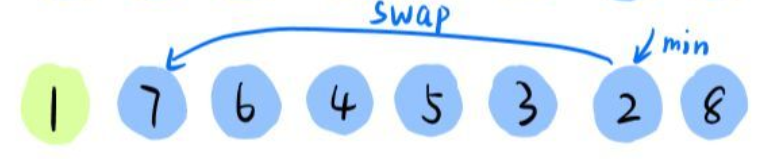
- 一种实现方式:

- 最好:O(n^2),最坏:O(n^2)
- 每次选择最小的元素交换
- 冒泡排序(稳定)
- 每次比较相邻元素并交换

-

- 最好O(n) 最坏O(n^2)
- 每次比较相邻元素并交换
- 归并排序(稳定)
- 平均、最好、最坏:O(nlogn)
- 分+排+合
- 每次合并都要用到一个临时数组,之后将数据拷贝到原数组
- 快速排序(不稳定)
- 平均时间复杂度是?O(nlogn),最坏情况下的时间复杂度是?O(n^2)
- 每次选择第一个为基准数,两个哨兵i、j,每次先移动j;递归
- 计数排序(可以稳定,可以不稳定)
- 不稳定:用额外的数组记录输入数据中各数据出现的次数,然后将数据按出现频数取出
- 稳定:将count改为累计,使用临时数组存储结果,反向填充数组
- 桶排序(稳定)
- 桶代表的是一个区间范围。将数组分配到有限量的桶里,然后对每个桶分别进行排序。
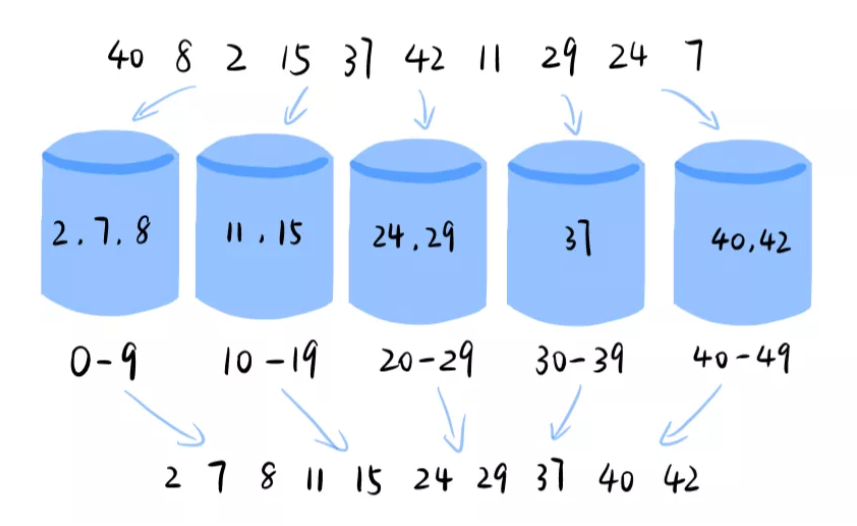
- 数组元素n,m个桶。平均每个桶的元素个数为k = n/m个。如果在桶内我们使用快速排序,总的时间复杂度即为nlog(n/m)。如果桶的数量接近元素的数量,桶排序的时间复杂度就是O(n)?了。如果所有的元素都到了一个桶了,时间复杂度退化成?O(nlogn)?。
- 桶代表的是一个区间范围。将数组分配到有限量的桶里,然后对每个桶分别进行排序。
- 基数排序(稳定)
- 整数排序算法,将整数按位切割成不同的数字(分桶),然后按每个位数分别比较。
- 设定10个桶,分别存放位数为0-9的元素。
- 遍历初始序列,将元素放入不同的桶中
- 按照桶的顺序,把桶中元素全部拿出来重新组装成一个序列
- 重复2、3步骤,直到最高位。即可完成排序
- 设待排序列为n个记录,序列中最大值的位数为d,数字的基数为 r,则进行链式基数排序的时间复杂度为O(d(n+r))。
- 整数排序算法,将整数按位切割成不同的数字(分桶),然后按每个位数分别比较。
- 希尔排序(改进的插入排序,不稳定)
- 把序列按一定间隔分组,对每组使用直接插入排序;随着间隔减小,一直到1,使得整个序列有序
- 时间复杂度复杂
- 堆排序(不稳定)
- 建堆:从最后一个非叶结点开始shift_dowm
- pop:最后一个结点提到根部,shift_down根节点
- 最好最坏以及平均情况下的时间复杂度均为O(nlogn)
- 插入排序(稳定)
- 综述
- P问题、NP问题
- P问题:Polynomial-time问题,能够在多项式时间内用算法求解的问题
- NP问题:非确定型多项式时间(nondeterministic polynomial-time)问题,指不确定是否存在多项式时间的求解算法,但可以在多项式时间内验证一个猜测解的正确性的问题
- 任意一个NP完全问题如果能够在多项式时间内解决,则所有的NP问题都能在多项式时间内解决
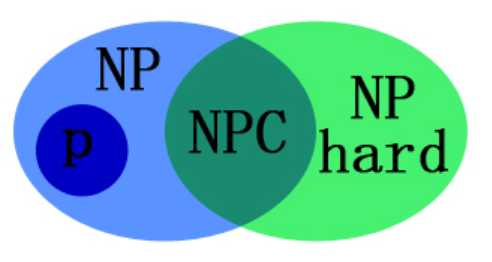
- NPC类问题(Nondeterminism Polynomial complete),指所有NP问题都能在多项式时间复杂度内归约到的NP问题
- NP难问题,指所有NP问题都能在多项式时间复杂度内归约到的问题
-
- 主方法
- 求解递推式的时间复杂度

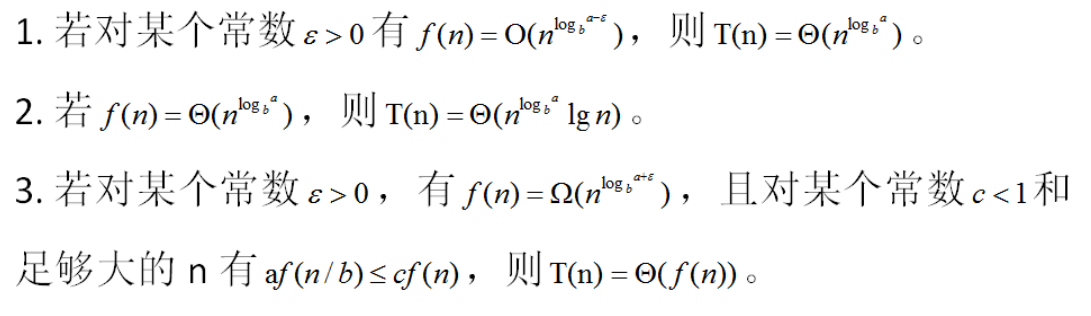
- 求解递推式的时间复杂度
- 最短路径算法
- Dijkstra
- 求单源、无负权的最短路
- 松弛操作
- 时间复杂度O(n^2)
- Floyd
- 求多源、无负权边的最短路
- 从i号顶点到j号顶点只经过前k号点的最短路程

- Bellman-Ford
- 求单源最短路,可以判断有无负权回路
- 就是我小班课讲过的东西:在每次的遍历过程中,对所有的边进行遍历判断

- Dijkstra
- 无序数组寻找中位数
- 线性选择算法:快排递归处理划分的两边,而线性选择只对其中的一个部分进行处理。具体步骤为:
- A[p...r]通过随机划分函数得到枢轴q
- 根据划分的两个区间A[p...q-1],A[q],A[q+1...r]
- 然后判断<=A[q]的元素数量k=q-p+1 与 需要寻找的第i小的关系,决定处理左面还是右面
- O(n)
- 线性选择算法:快排递归处理划分的两边,而线性选择只对其中的一个部分进行处理。具体步骤为:
- 最长公共子序列
- c[i][j]表示串1前i个字符、串2前j个字符的最长公共子序列长度
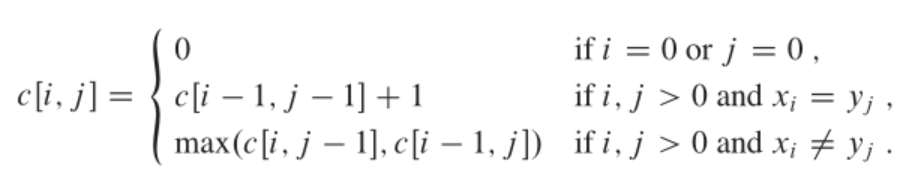
- 如果想要得到串本身:
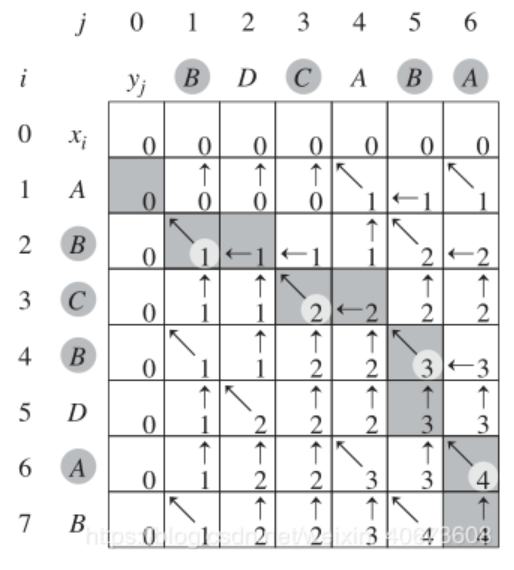
- 在对应字符相等的时候,用↖标记
- 在p1 >= p2的时候,用↑标记
- 在p1 < p2的时候,用←标记
- c[i][j]表示串1前i个字符、串2前j个字符的最长公共子序列长度
- 最长公共字串
- 当A[i] != B[j],dp[i][j] = 0
- 当A[i] == B[j],
- 若i = 0 || j == 0,dp[i][j] = 1
- 否则?dp[i][j] =?dp[i - 1][j - 1] + 1
- 01背包问题
-
- 卡特兰数
- 适用题型:有一个大问题A,规模为n,要解决这个问题,可以用分治的思想,首先固定其中某一个元素,将剩下的n-1个元素拆分成两个小问题,这两个小问题的规模分别是(0,n-1) (1,n-2) (2,n-3) ... (n-1,0)
- 如:
- 二叉树计数,n个结点的二叉树,首先固定根节点,将剩下的n-1个结点拆分给左右子树
- 从1到n可以构建的BST的数目
- 三角形划分问题,凸(n+2)边形可以划分为n个三角形,首先固定一条边(即一个三角形),这个三角形将这个(n+2)边形拆分成两个更小的多边形
- 递推式:
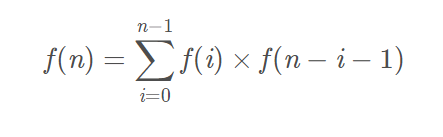
- 通项公式:
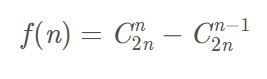
- 第K大的数
- 借助最小堆,保持堆的大小为K,O(nlogk)
- 基于快速排序,只关注位置k,o(n)
