一、前言
? ? ?在上一篇《数据结构内功修炼之线性表》中,采用了中规中矩的方法。文章是很长的,但是认真看下来你会发现——真的长!不过也难怪嘛,线性表里面顺序表和链表本来就是一切的基石,所以很多基本问题自然是要仔仔细细看的,当然看严蔚敏老师的书也更好。所以这一片博客,让我们在规矩的结构上,大胆各种发挥一波。???
? ? ?按照惯例给出本章的知识结构吧!

? ? ?你可能会对一些名词奇怪,例如什么是共享栈?什么是双端队列,这里不是说栈和队列吗,为什么谈到了数组?——别担心,让我们一起往下思考
二、栈
? ? ?定义:栈(Stack)是限定在表尾进行插入或删除操作的限定表。表尾端称为栈顶,表头端称为栈底(就是允许插入删除的那一端称为栈顶,不允许的那一端称为栈底,空栈就是不含任何元素的空表)。
? ? ?逻辑结构:操作受限的线性表
? ? ?存储结构:有顺序存储也有链式存储
? ? ?运算:初始化、判断非空、出栈、入栈、读栈顶元素、销毁栈。
1、顺序栈的一些操作思考。
(1)关于初始化栈顶指针的问题?
? ? ?你有没有想过,利用顺序表来操作栈的话肯定是要有栈顶指针来执行栈顶元素的,方便我们实现出栈、入栈、判空等重要的操作。假如顺序栈的引用设为S,那么初始化栈头指针是S.top=-1还是S.top=0呢?
? ? ?如果这两者有其中之一比较好,那就不会两个都存在,但不管是S.top=-1还是S.top=0,性质都是一样的。可是呢,不同的定义往往会影响操作。那么我们来看看,对于两者到底有什么区别呢?
- 初始化
? ? ?在严蔚敏老师的课本中,S.top表示栈顶元素在顺序栈中的位置,并且她让栈顶元素初始化为S.top=0。为了用C语言描述时更加方便,所以也引入了S.base指针,也就是初始化就指向栈底,之后一直不变的指针。这样判空就为S.top=S.base。而初始化的代码为:
Status InitStack(SqStack &S)
{
S.base = new SElemType[MAXSIZE];
if(!S.base) exit(OVERFLOW);
S.top = S.base;
S.stacksize = MAXSIZE;
return 0;
}? ? ?而当我们初始化S.top=-1时,初始化代码可以简单的写出这样(省略了S = new SElemType[MAXSIZE]这样的代码):
void InitStack(SqStack &S)
{
S.top = -1;
}? ? ?从这里是看不出区别的,但是我们往下看:
- 入栈
? ? ?S.top=0的情况
Status Push(SqStack &S,SElemType e)
{
if(S.top-S.base==S.stacksize) return ERROR;//栈满
*S.top++=e;//先将元素压入栈,再栈顶指针加一
return OK;
}? ? ?S.top=-1的情况
bool Push(SqStack &S,ElemType x) {
if(S.top==MaxSize-1)//栈满
return false;
S.data[++S.top]=x;//指针先加一,再入栈
return true;
}
? ? ?我们发现当S.top=0时,我们在入栈的时候直接先赋值,栈顶指针再加一;而S.top=-1时,我们先栈顶指针加一,再赋值。难道这有什么规律吗?——
? ? ?不!没有任何规律,你只要画画图就能够明白,这个问题毫无价值。

- 出栈
? ? ?那么出栈呢?当S.top=0时,出栈不就是先让栈顶指针减一,然后把值拿出去;当S.top=-1时,出栈不就是直接拿出去,然后栈顶指针再减一吗?有图有真相:

- 取栈顶元素
? ? ?取栈顶元素指针当然不变啦,不同的是因为初始化栈顶指针的不同,所以对于S.top=0这样的初始化来说,x=S.data[S.top-1]就好,而对于S.top=-1这样的初始化来说,x=S.data[S.top]就好。
2、共享栈
? ? ? ? ? 利用栈底位置相对不变的特性,可以让两个顺序栈共享一个一维数组空间,将两个栈的栈底分别设置在共享空间的两端,两个栈顶向共享空间中间延伸。

? ? ?两个栈的栈顶指针都指向栈顶元素,top0=-1时0号栈为空,top1=MaxSize时1号栈为空(这里我们初始赋为-1类似的情况);仅当两个栈顶指针相邻(top1-top0=1)时,判断为栈满(例如0号栈到了2,1号栈到了3,不就满了吗?)。当0号栈进栈时top0先加一在赋值,1号栈进站时top1先减1在赋值;出站时刚好相反。
3、关于链栈的一些思考
? ? ?这里我们采用没有头结点的链表来表示栈,入栈和出栈操作都在链表的表头进行。那么我们需要注意什么呢?
(1)链栈的出栈
? ? ?如果你熟悉链表的操作的话,你会知道入栈也就是在表头添加结点是很简单的(如果你还记得我招小弟的说法,也就是新插入的结点指向L,然后这里是将L的指针移到插入的结点即可),但是不管是从表头删除结点还是从其它的位置删除,我们都需要注意一件事情,你猜是什么?
? ? ?当然是保存要要出结点的指针,以备释放啦,所以会有类似出栈的代码如下:
Status Pop(LinkStack &S,SElemType &e)
{
if(S==NULL) return ERROR;
e=S->data;
p=S;
S=S->next;
delete p;
return OK;
}? ? ?解读一下上面的代码,不就是先判断是否为空,然后得到值,利用P指针保存当前栈顶,将下一个结点变为首元结点,然后释放原栈顶元素的空间即可。
二、队列
? ? ?队列(Queue)简称队,也是一种操作受限的线性表,只允许在表的一端进行插入,而在表的另一端进行删除。向队列中插入元素成为入队或进队;删除元素称为出队或离队(先进先出First In First Out,FIFO)。
逻辑结构:操作受限的线性表
物理结构:可以用顺序表实现,也可以用链表实现
运算:初始化队列、判队列空、入队、出队、读队头元素
? ? ?好的,现在我们手里有两个工具,数组和链表。需要实现上面特点的数据结构,你会怎么做呢?
1、队列的顺序存储
? ? ?如果要利用顺序表去实现这个功能,那么队头和队尾肯定需要有指针来指示操作的,并且我们需要设定初始情况,入队、出队以及判空,判断是否队列已满等情况的代码。给出顺序存储结构的表如下:
#define MAXQSIZE 100
typedef struct
{
QElemType *base;
int front;
int rear;
}SqQueue;? ? ?拥有了这样的结构,那么我们初始化front=rear=0,然后入队的时候只需要插入新元素,然后尾指针加一;出队的时候只需要将头指针front加一。因此在非空队列中,头指针始终指向队头元素,而尾指针始终指向队尾元素的下一个位置。但是会出现这样的情况!!!

? ? ? 我们发现如果再次添加就满了,判断是否满了如果用rear=MAXSIZE是可以组织上面的情况发生的(假溢出),但很明显我们空间还有很多,所以,我们肯定要想办法把空间利用起来,比如让rear指针添加的时候到第0个位置不就好了吗,那肯定是取模的方法可以办到。也就是说入队的时候我们指针变化有rear = (rear+1)%MAXSIZE;这样上面的情况就是rear = (3+1)%4 = 0,尾指针就到下面来了。
? ? ?所以对于运算指针的变化依旧有:
- 初始时Q.front = Q.rear = 0;
- 入队Q.rear = (Q.rear+1)%MAXSIZE;
- 出队Q.font = (Q.front+1)%MAXSIZE;
- 队列长度(Q.rear-Q.front+MAXSIZE)%MAXSIZE;(长度本来就可以用rear-front,但是当我们采用循环的时候可能减出来是负值,所以加一个MAXSIZE上去,在取余)
- 判队列满???
? ? ?(1)我们用增设表示元素个数的数据成员,当Q.size=MAXSIZE就满了。
? ? ?(2)但是大多采用的都是牺牲一个单元来区分队空和队满,入队时少用一个队列单元,约定“队头指针在队尾指针的下一位置作为队列满的标志”。这里很好理解,你想啊,现在我们的队尾指针一直都是指向队尾元素的下一个,也就是说它当前的位置是空的,而下一个位置如果是队头指针的话,当然为空啦!
? ? ?所以判断的表达式不就是(rear+1)%MAXSIZE = front用来判断队满吗,而队空一直没有变,就是front=rear。
2、链式队列
? ? ?顺序的实现了,你想来试试链式队列???
? ? ?队列的链式表示成为链队列,实际上是一个同时带有队头指针和队尾指针的单链表。头指针指向队头结点,尾指针指向队尾结点,即单链表的最后一个结点。
? ? ?我们在设置链栈时,采用的是不设置头结点的链表形式,这里我们需要采用带头结点的链表来实现,为什么呢?你想啊,我们总是在头结点删除,如果不设置头结点的话,总是需要去找到首元结点(也就是当前要出队删除的结点的下一个结点记住它的指针来实现),而有了头结点,直接头结点指向下一个结点就实现了,多方便呀)。所以关于链队,没有啥说的,但一定要注意链表的插入和删除操作,必要时画图帮助理解。
3、双端队列
? ? ?双端队列是指允许两端都可以进行入队和出队操作的队列。其元素的逻辑结构仍然是线性结构,队列的两端分别成为前端和后盾,两端都可以入队和出队。
? ? ?这里我们需要了解两个概念即可,其它的,画图都是可以解决的。
? ? ?输出受限的双端队列:允许在一端进行插入和删除,但在另一端只允许删除的双端队列称为输出受限的双端队列。
? ? ?输入受限的双端队列:允许在一端进行插入和删除 ,但在另一端只允许删除的双端队列称为输入受限的双端队列。
三、数组(特殊矩阵的压缩存储)
? ? ?在高级语言中,数组我们在熟悉不过。这里可以给出一个简短的定义:
? ? ?数组是由n(n>=1)个相同类型的数据元素构成的优先序列,每个元素称为一个数组元素,每个元素在n个线性关系中的序号称为该元素的下标,下标的取值范围称为元素的维界。
? ? ?为什么在这里要提到数组,因为它其实也是线性表的推广。一维数组可以视为一个线性表;二维数组可以视为其元素也是定长线性表的线性表。
? ? ?那,我们这里会介绍关于数据的小标存储关系吗?不会,这里要知道的是特殊举证的存储。
? ? ?矩阵充满了现在计算机的应用,而矩阵的存储当然十分的重要。现在我们思考,除了一般的矩阵我们需要一一存储,特殊的矩阵如果在一一存储的话不就浪费了巨大的空间吗?所以我们需要了解如何去压缩存储。
1、对称矩阵
? ? ?用线性代数的方法来说,对称矩阵就是矩阵转置之后等于本身的矩阵。但这显得抽象,而我们给出对一个n阶方阵A[1...n][1...n]中的任意一个元素aij都有aij = aji(1<=i,j<=n),则称为对称矩阵。这个时候你的脑中应该有一条对角线,线的两侧的元素都是对称的(例如y=x线对称)。
? ? ?Why?对于对称矩阵来说,如果我们直接用二维矩阵存储元素,那么会浪费几乎一般的空间(大概是(n^2-n)/2空间)。所以我们可以选择只存储对角线及其上半部分或者下半部分的元素,这样看空间就节省下来了,那么怎么存储呢?
? ? ?首先我们需要一个一位数组空间B[n(n+1)/2]即可。
(1)存
? ? ?存的时候我们可以直接利用双重的for循环把数据存到一位数组空间B中,例如代码:
for(i=1;i<n;i++)
for(j=1;j<i+1;j++)
B[k++] = a[i][j]? ? ?这样我们就将原本存储在二维数组a中的数据存到了B中,但是要怎么取呢??
(2)取
? ? ?如果要从B中取a[i][j]这个元素,我们会发现有这样的下标关系:
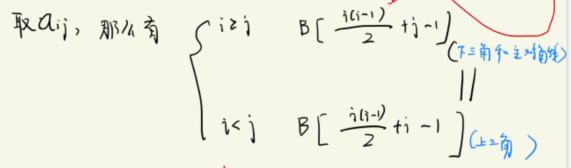
? ? ?所以只需要带入i,j的值到B下标关系中,就可以取到相应的元素值(只需要推到一侧的,因为是对称矩阵,所以i<j时情况一致)。如果你自己手动的推到一下就会发现,这只是简单的等差数列求和的公式,即使记不住,现场推导也是可以的。
2、三角矩阵
? ? ?定义:三角矩阵有下三角矩阵和上三角矩阵。
1)下三角矩阵
? ? ?(1)存
? ? ? ? ? 存的时候我们依旧可以利用上面的方法,将二维数组里面的元素存到一维数组B中。这里二维数组指的形式,不是真的先存到二维数组中再去转存到一维数组,这样空间节约在哪里呢?而是说我们有形如这样的二维数组,然后存到一维数组中就好,这样就压缩存储了。取出来的时候根据下标关系就可以了,也就实现了节省空间的做法。
? ? ?(2)取

? ? ?这里我省略推到的过程,因为下三角矩阵的推到关系和对称矩阵一致,不同的是之前在对称矩阵中我们申请的是B[n(n+1)/2]的数组,而下三角矩阵需要多一个来存储同一常量(例如0啥的),所以就有了上式。
2)上三角矩阵
? ? ?(1)存:~~~~~~~~~~~~~~~~~~~~~·存进去即可,存到一个一维数组节省空间。
? ? ?(2)取:
? ? ?这里我们可以一起来推到一下去aij的关系式情况,我们仅仅需要知道aij是在B数组中第几个就好,按行存储,所以:
当i<=j时,也就是上面的右上角部分的关系如下:
第一行:n个元素
第2行:n-1个元素
...
第i-1行:n-i+2个元素
第i行:j-i个元素
所以等差数列求和不就有(i-1)(2n-i+2)/2+(j-i)。而i>j时,最后一个位置存放即可。

3、三对角矩阵
? ? ?定义:对角矩阵也称为带状矩阵。对于n阶方阵A中的任一元素aij,当|i-j|<1时,有aij=0(1<=i,j<=n),则称为三对角矩阵,上图!

? ? ?(1)存:~同上
? ? ?(2)取
? ? ? ? ? 三对角矩阵取的话,我没有找到很好的规律,所以就给出结果吧,但有趣的是反取。也就是知道B数组中的位置,去找aij。

4、稀疏矩阵
? ? ?至于稀疏矩阵的存储,我们可以采用三元组的方式,也可以采用十字链表法存储。这里不再赘述,给出一张三元组的图片就知道有多么便捷了。

总结:
? ? ? 栈、队列和数组及其的重要,我们要熟悉它们的逻辑结构、存储结构和运算,冲冲冲!