[数据结构与算法]【数据结构】线性表

《数据结构（第二版）》清华大学出版社,严蔚敏,吴伟民 编.

线性表的逻辑结构

线性表是一种数据结构，一个线性表是 n 个数据元素的有限序列。关系N是一个序偶的集合，它表示线性表中数据元素之间的相邻关系，即 a_i-1 领先于 a_i，a_i 领先于 a_i+1。

稍复杂的线性表中，一个数据元素可以由若干个数据项组成，把数据元素称为记录，含有大量线性表称为文件。数据元素可以是各种各样的，但同一线性表中的元素必定具有相同特性，因此属于统一数据对象。

一个学校的学生健康情况文件，每个学生的情况为一个记录，由姓名、学号、性别、年龄、班级和建康状况等六个数据项组成。

对线性表进行的基本操作：

1. INITIATE(L) 初始化操作。设定一个空的线性表 L。
2. LENGTH(L) 求长度函数。函数值为给定线性表 L 中数据元素的个数。
3. GET(L,i) 取元素函数。若 $1\le i\le LENGTH(L)$，则函数值为给定线性表 L 中第 i 个数据元素，否则为空元素 NULL。称 i 为该数据元素在线性表中的位序。
4. PRIOR(L,elm) 求前驱函数。已知 elm 为给定线性表 L 中的第一个数据元素，若它的位序大于 1，则函数值为 elm 的前驱，否则为空元素。
5. NEXT(L,elm) 求后继函数。已知 elm 为给定线性表 L 中的一个数据元素，若它的位序小于 LENGTH(L)，则函数值为 elm 的后继，否则为空元素。
6. LOCATE(L,x) 定位函数。给定值 x，若线性表 L 中存在其值和 x 相等的数据元素，则函数值为该数据元素在线性表中的位序，否则为零。
7. INSERT(L,i,b) 前插操作。在给定线性表 L 中第 i 个数据元素之前插入一个新的数据元素 b。
8. DELETE(L,i) 删除操作。删除给定线性表 L 中第 i 个数据元素。
9. EMPTY(L) 判空表函数。
10. CLEAR(L) 表置空操作。操作结果将 L 置为空表。

线性表的顺序存储结构

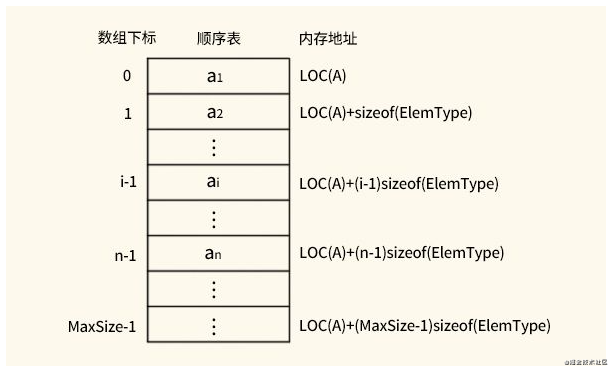
用一组地址连续的存储单元依次存储线性表的元素，逻辑关系上相邻的两个元素在物理位置上也相邻。

假设线性表的每个元素需要占用 l 个存储单元，并以所占的第一个单元的存储地址作为数据的存储位置。一般来说，线性表的第 i 个元素 a_i 的存储位置为：

$$LOC(a_i)=LOC(a_i)+(i?1)?l$$

式中$LOC(a_1)$是线性表的第一个数据元素$a_1$的存储位置，通常称作线性表的起始位置或基地址。它的特点是为表中相邻的元素$a_i$和$a_{i+1}$赋以相邻的存储位置$LOC(a_i)$和$LOC(a_{i+1})$。换句话说，以元素在计算机内物理位置相邻来表示线性表中数据元素之间的逻辑关系。只要确定了存储线性表的起始位置，线性表中任一数据元素都可随机存取，所以线性表的顺序存储结构是一种随机存取的存储结构。

在顺序结构的线性表中某个位置插入或删除一个数据元素时，其时间主要耗费在移动元素上，而移动元素的个数取决于插入或删除元素的位置。

线性表的链式存储结构

线性表的顺序存储结构有三个弱点：1. 在做插入操作时需要移动大量的元素；2. 预先分配空间时，必须按最大空间分配；3. 表容量难以扩充；

用一组任意的存储单元存储线性表的数据元素，存储单元可连续可不连续。数据元素的存储映像称为结点（数据域+指针域），n 个结点链成一个链表。

整个链表的存取必须从头指针开始进行，头指针指示链表中第一个结点的存储位置，由于最后一个数据元素没有直接后继，则线性链表中最后一个结点的指针为空。

用线性链表表示线性表时，数据元素之间的逻辑关系由结点中的指针指示，逻辑上相邻的两个数据元素其存储的物理位置不要求相邻。

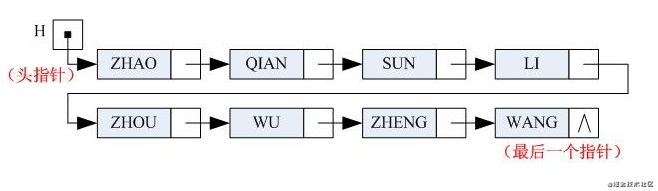
循环链表

另一种形式的链式存储结构。其特点是表中最后一个结点的指针域指向头节点，整个链表形成一个环。从表中任一结点出发均可找到表中其它结点。

循环表与线性链表基本一致，差别仅在于循环条件判断为是否等于头指针。

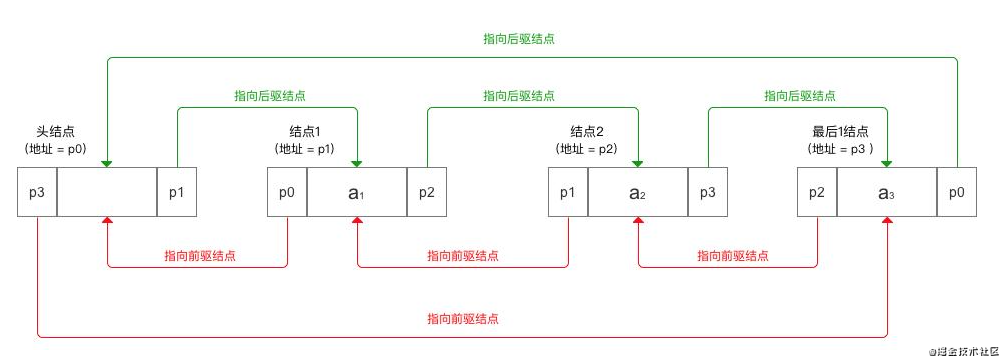
双向链表

为了克服单链表的单向性缺点，产生了双向链表。在双向链表中，节点有两个指针域，一个指向直接后继，另一个指向直接前驱。

双线链表亦可有双向循环链表。