?机器学习之支持向量机（SVM）
SVM 分类模型
? ? ? ?支持向量机（Support Vector Machine, SVM）是一类按监督学习方式对数据进行二元分类的广义线性分类器。是Corinna Cortes和Vapnik8等于1995年首先提出的，它在解决小样本、非线性及高维模式识别中表现出许多特有的优势。 ? ? ? ? ? ? ?
? ? ? ?SVM的的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。使用铰链损失函数（hinge loss）计算经验风险，并在求解系统中加入了正则化项以优化结构风险。
SVM模型构建：间隔最大化的数学表示
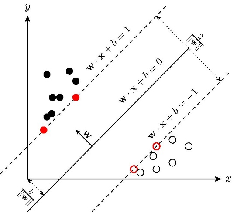
- 条件是
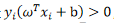，那么? γ>0 , 函数间隔 
。最小间隔等于γ，因此所有的数据点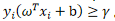
。 - 对ω和b同乘n，函数边界γ也会乘以n，有无数解。引入γ=1使得间隔是确定的，此时的间隔称为几何间隔。
- 等价转换，可以得到带约束条件的最优化问题。
?
硬间隔SVM：模型求解之KKT条件：
- KKT条件是不等式约束使用拉格朗日乘数法的必要条件，当原问题是凸问题的时候，也是充分条件。KKT条件是强对偶性的充要条件，是有最优值的必要条件，是拉格朗日乘子法的泛化。
- KKT条件中的松弛互补条件 λ_i(1?y_i(ω^Tx_i+b))=0，对于支持向量来说1?y_i(ω^Tx_i+b)=0，则λ_i可以取非零值；但对于其他点来说1?y_i(ω^Tx_i+b)≠0，那么λ_i必然为0。
?
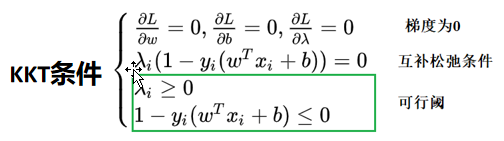
?硬间隔SVM：模型转换：
- 约束条件g(ω) ≤0把ω空间划分为两部分：g(ω)>0 即不满足约束部分，g(ω)≤0满足约束的部分。由于λi≥0，g(ω)>0时，λi g(ω)在λ空间最大值为无穷大；g(ω)≤0时，当λi=0时，λi g(ω)在λ空间最大值为0。
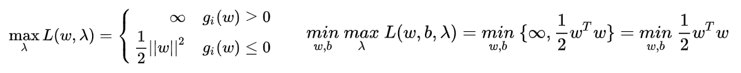
- 故最优化问题转换为：
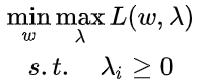
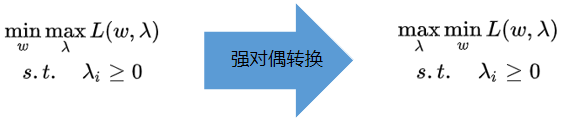
硬间隔SVM：强对偶关系转换
- 弱对偶关系 ：min max L ≥ max min L
- 强对偶关系：min max L = max min L
- 凸优化问题都是强对偶的。（二次函数目标函数+线性约束）是凸优化问题。
?
?硬间隔SVM： SMO求λ
- SMO(Sequential Minimal Optimization) 序列最小优化算法求解。核心思想：优化目标有约束条件没法一次只变动一个参数，所以一次选择两个参数；每次只优化一个参数，其他参数先固定住，仅求当前这个优化参数的极值。SMO步骤如下：
- 利用∑_i=1^n?λ_iy_i=0，选择两个需要更新的参数λi、λj，固定其他参数。相当于把目标问题转化成了仅有约束条件λi≥0的最优化问题。于是约束就变成了：
? - 在λi上对优化目标求偏导，令导数为零，从而求出变量值λinew，带入得到λjnew。
- 反复执行上述步骤，直到所有乘子满足KKT条件或参数的更新量小于设定值。
硬间隔SVM：求解b、最终结果
- 只有在支持向量上才有λ>0，其他λ=0，因此ω、b的值只和支持向量有关。随便找个支持向量，把前面得到的ω带入：
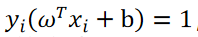，即可得到b。为了b更具鲁棒性，可以求支持向量的均值。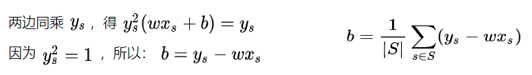 
- 先求λ，得到支持向量，再得到ω、b 。
- ?分类决策函数：
?
?
?
?
?
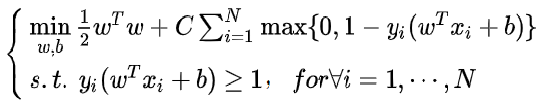
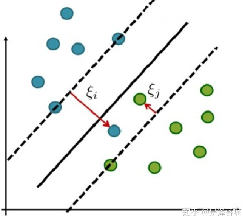
- ?ξ也叫松弛变量。大于等于0的ξ和0求最大值，肯定等于ξ，所以去掉了max。
- 超参数C>0，可以理解为错误样本的惩罚程度。若C为无穷大， ξ必然无穷小，就变成了硬间隔 SVM；当 C 为有限值时，才会允许部分样本不遵循约束条件。
- 没离群的点松弛变量都等于0。
?
核函数
- 很多数据不是线性可分的。以著名的非线性可分异或问题为例：
- ?Cover定理：将复杂的模式分类问题非线性地投射到高维空间，将比投射到低维空间更可能是线性可分的。即维度越高，线性可分的可能性越高。
- 将非线性可分的数据集通过一个非线性转换函数?(x)映射到高维空间转换为线性可分数据。
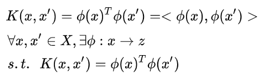
- ?可以把核 K (x, z) 理解成对φ(x) 和 φ(z) 的近似程度的一种度量手段。 能够写成仅用输入属性向量的内积来表达的算法，那么就可以通过引入 核K（Kernel）。
- 径向基函数(Radial Basis Function 简称 RBF）核也被称为高斯核，首选。
?
?核函数：应用于SVM
?SVM用于多分类
- ?一次性考虑所有样本，并求解一个多目标函数的优化问题，计算量实在太大，不实用。
- 一对多法（one-versus-rest,简称OVR SVMs）：训练时依次把某个类别的样本归为一类，其他剩余的样本归为另一类，每次仍然解一个两类分类的问题，k个类别的样本就构造出了k个SVM，最终取置信度最大的一个作为分类结果。好处是每个优化问题的规模比较小，而且分类的时候速度很快。人为的造成了 “数据集偏斜”问题。
- 一对一法（one-versus-one,简称OVO SVMs）：在任意两类样本之间设计一个SVM，因此k个类别的样本就需要设计k(k-1)/2个SVM。最后得票最多的类别作为分类结果。虽然分类器的数目多了，但是在训练阶段所用的总时间却比“一类对其余”方法少很多。Libsvm的多类分类就是根据这个方法实现的。
?SVM工具：libsvm
- libsvm是台湾大学林智仁(Chih-Jen Lin)教授2001年开发的一套实现支持向量机的库。特点：程序小，文档详细，运用灵活，输入参数少，开源的，目前国内应用最多的SVM的库。
- OpenCV2-4的SVM：基于libsvm 2.6版，C++实现了最优参数自动搜寻等功能。 libsvm最新版为3.25。
- 官网：https://www.csie.ntu.edu.tw/~cjlin/index.html
- README：使用说明。?
- svm.cpp/svm.h：svm算法的具体实现文件。
- SVM-toy：分类界面可视化的工具。?
- subset.py：将样本集合按比例抽样出两个子样本集合。
- easy.py：网格参数寻优。
SVM工具：训练技巧
- K折交叉验证（K-fold cross-validation：初始采样分割成K个子样本，一个单独的子样本被保留作为验证模型的数据，其他K-1个样本用来训练。交叉验证重复K次，每个子样本验证一次，平均K次的结果。k折一般常用为5-10。
- 获取较好的模型：1. 对数据做归一化；2. 应用 RBF kernel ；3. 用cross-validation和grid-search 得到最优的c和g；4. 用得到的最优c和g训练训练数据。
- 在特征数或样本很多时，推荐使用线性核，推荐使用liblinear。
- 数据集偏斜：参与分类的各个类别样本数量差异很大。给样本数量少的类别更大的惩罚因子，libSVM直接使用样本数量的比。
SVM工具： liblinear
- liblinear是一个简单的求解大规模规则化线性分类和回归的软件包。最大的特点是速度快！ 多分类：liblinear多类分类时采取one vs rest方法。
- 和libsvm的差异：模型文件格式不兼容；线性模型时，两者的目标函数不一样；liblinear比libsvm快很多；准确率接近。
- solver_type ：L2R_LR使用predict_probability ; ?L2R_L2LOSS_SVC_DUAL使用predict。
一、什么是SVM（支持向量机）？
支持向量机为一个二分类模型,它的基本模型定义为特征空间上的间隔最大的线性分类器。而它的学习策略为最大化分类间隔,最终可转化为凸二次规划问题求解。
1.1、SVM（支持向量机）与LR（逻辑回归）的区别?
LR是参数模型,SVM为非参数模型。LR采用的损失函数为logisticalloss,而SVM采用的是hingeloss。在学习分类器的时候,SVM只考虑与分类最相关的少数支持向量点。LR的模型相对简单,在进行大规模线性分类时比较方便。
1.2、SVM中什么时候用线性核什么时候用高斯核???
当数据的特征提取的较好，所包含的信息量足够大，很多问题是线性可分的那么可以采用线性核。若特征数较少，样本数适中，对于时间不敏感，遇到的问题是线性不可分的时候可以使用高斯核来达到更好的效果。
1.3、SVM的作用，基本实现原理。
SVM可以用于解决二分类或者多分类问题，此处以二分类为例。SVM的目标是寻找一个最优化超平面在空间中分割两类数据，这个最优化超平面需要满足的条件是：离其最近的点到其的距离最大化，这些点被称为支持向量。
解析：建议练习推导SVM，从基本式的推导，到拉格朗日对偶问题。
1.4、SVM的硬间隔，软间隔表达式；
?
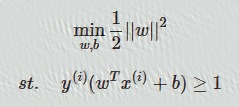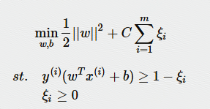
左边为硬间隔；右边为软间隔
解析：不同点在于有无引入松弛变量（）
1.5、SVM使用对偶计算的目的是什么，如何推出来的，手写推导。
目的有两个：一是方便核函数的引入；二是原问题的求解复杂度与特征的维数相关，而转成对偶问题后只与问题的变量个数有关。由于SVM的变量个数为支持向量的个数，相较于特征位数较少，因此转对偶问题。通过拉格朗日算子发使带约束的优化目标转为不带约束的优化函数，使得W和b的偏导数等于零，带入原来的式子，再通过转成对偶问题。
1.6、SVM的物理意义是什么？
构造一个最优化的超平面在空间中分割数据。
1.7、如果数据有问题，怎么处理；
（1）上下采样平衡正负样例比；（2）考虑缺失值；（3）数据归一化。