1.线性回归中的相关度和决定系数
协方差反映的是两个随机变量间的相关关系。如果同步增大,则协方差为正。

?皮尔逊系数就是协方差除以两个随机变量的方差,相关度越高,皮尔逊系数将会趋于1/-1。
R平方叫做决定系数,反应因变量变异程度可以通过回归关系被自变量解释的比例。
局限性:随着自变量增加,R平方一定会增加。
2.最小二乘

?3.因果识别
举一个例子来说明:读大学并拿到本科学位对收入有什么影响?
对于某个特定的个人,我们需要知道两件事:1)这个人读大学并拿到本科学位之后的收入;2)让这个人穿越回要上大学之前的那个节点,不上大学,直接去工作的收入。用1)减去2)就是这个人读大学并拿到本科学位对他 ∕ 她本人收入的影响。
对于某群人,我们同样需要知道两件事:1)这群人读大学并拿到本科学位之后收入的均值;2)让这群人都穿越回各自上大学之前的节点,不上大学,直接去工作的收入的均值。同样用1)减去2)。
所以想要得到因果识别的结果,最关键的一点就是得到对照组(counter-factual),也就是上面列出的2)代表的结果。
3.大数定理和中心极限定理
大数定理:当样本数量足够大时,这些样本的均值无限接近总体的期望。??
中心极限定理:不管样本总体服从什么分布,当样本数量足够大时,样本的均值以正态分布的形式围绕总体均值波动。
4.双重差分法DID
由于"人不可能同一次踏入第二条河流"那么我们需要找到一个(群)人与研究对象对象是完全相同的,直到发生了某事件.
什么叫DID呢?就是我在一个事件发生之前,这两者长得是完全一样,或者不一定完全一样,只要红线与绿线平行就成。但是到了这件事情发生以后,它的平行趋势扩大了。那么大家想,原来两者之间就有一个difference(差分),但是现在两者差距进一步拉大,那么我们将扩大以后的差别,减掉之前的差别,是不是就是difference in difference。这就告诉我们,这件事情的冲击对你要研究的对象产生了多大的影响。

5. 多重共线性的检验与处理
多重共线性(Multicollinearity)是指线性回归模型中的解释变量之间由于存在较精确相关关系或高度相关关系而使模型估计失真或难以估计准确(无法估计或参数估计方差无限大)。完全共线性的情况并不多见,一般出现的是在一定程度上的共线性,即近似共线性。可以用T检验检出多重共线性问题.
解决多重共线性问题大致上有以下方法:去掉次要变量,改变变量的形式,差分法,逐步回归分析(F检验显著),主成分分析,偏最小二乘,岭回归.
6.岭回归
先考虑最小二乘有时可能出现数据维度大于样本数的情况.
可以看出目标函数是一个凸二次规划问题,其最优解在导数为0处取到,矩阵导数详细参考。
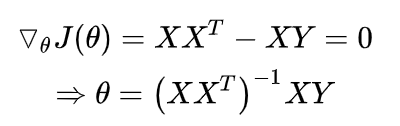
值得注意的上式中存在计算矩阵的逆,一般来讲当样本数大于数据维度时,矩阵可逆,可以采用最小二乘法求得目标函数的闭式解。当数据维度大于样本数时,矩阵线性相关,不可逆。此时最小化目标函数解不唯一,且非常多,出于这样一种情况,我们可以考虑奥卡姆剃刀准则来简化模型复杂度,使其不必要的特征对应的Ω为0,可以考虑0范数使得模型中Ω非0个数最少(实际上采用的是??范数的一个凸近似)。当然,岭回归,lasso回归的最根本的目的不是解决不可逆问题,而是防止过拟合。
岭回归的目标函数在一般的线性回归的基础上加入了正则项,在保证最佳拟合误差的同时,使得参数尽可能的“简单”,使得模型的泛化能力强。正则项一般采用一,二范数,使得模型更具有泛化性,同时可以解决线性回归中不可逆情况.
?Lasso回归采用一范数来约束,使参数非零个数最少。而Lasso和岭回归的区别很好理解,在优化过程中,最优解为函数等值线与约束空间的交集,正则项可以看作是约束空间。可以看出二范的约束空间是一个球形,一范的约束空间是一个方形,这也就是二范会得到很多参数接近 0?的值,而一范会尽可能非零参数最少。
?7.方差分析

8.异方差检验
违反了同方差假定,此时,有理由怀疑我们缺失了某个关键自变量.此时T检验失效,
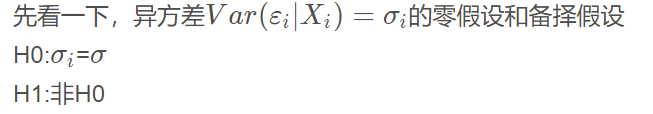
?先构造残差序列,之后映入辅助模型,作OLS后检验参数.
9.线性回归的六大假定

复习回归的步骤:①构造回归形式②求解参数③参数检验④模型整体检验(R方和F检验)
?
?
?
?