[数据结构与算法]集成学习chap2

1）详细阐述线性回归模型的最小二乘表达：
我们需要衡量真实值$y_i$与线性回归模型的预测值$w^T{x}_i$之间的差距，在这里我们和使用二范数的平方和L(w)来描述这种差距，即：
$$\begin{gathered} L(w)=\sum _{i=1}^N||w^T{x}_i?y_i|{|}_2^2=\sum _{i=1}^N(w^T{x}_i?y_i{)}^2=(w^T{X}^T?Y^T)(w^T{X}^T?Y^T{)}^T=w^T{X}^{T}Xw?2w^T{X}^{T}Y+Y{Y}^T \\ 因此，我们需要找到使得L(w)最小时对应的参数w，即： \\ \hat{w}=argminL(w) \\ 为了达到求解最小化L(w)问题，我们应用高等数学的知识，使用求导来解决这个问题： \\ \frac{?L(w)}{?w}=2X^{T}Xw?2X^{T}Y=0,因此： \\ \hat{w}=(X^{T}X{)}^{?1}{X}^{T}Y \end{gathered}$$ 2）在线性回归模型中，极大似然估计与最小二乘估计有什么联系与区别
最小二乘法以估计值与观测值的差的平方和作为损失函数，极大似然法则是以最大化目标值的似然概率函数为目标函数，从概率统计的角度处理线性回归并在似然概率函数为高斯函数的假设下同最小二乘建立了的联系。
3）为什么多项式回归在实际问题中的表现不是很好？
4）决策树模型与线性模型之间的联系与区别
5）什么是KKT条件

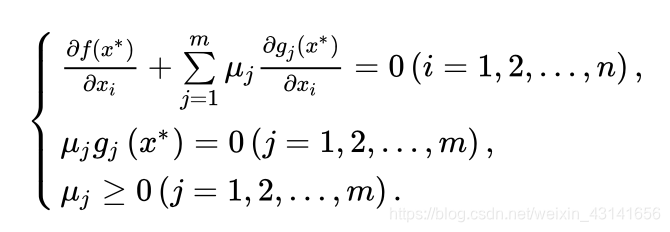
6）为什么要引入原问题的对偶条件
7）使用CH1机器学习数学基础所学的内容，找到一个具体的数据集，使用线性回归模型拟合模型，要求不能使用sklearn，只能使用python与numpy。

# compute loss
def compute_error_for_line_given_points(b, w, points):
    totalError = 0
    for i in range(len(points)):
        x = points[i, 0]
        y = points[i, 1]
        totalError += (y - (w * x + b)) ** 2
    return totalError / float(len(points)) # average

# compute gradient
def step_gradient(b_current, w_current, points, learningRate):
    b_gradient = 0
    w_gradient = 0
    N = float(len(points))
    for i in range(len(points)):
        x = points[i, 0]
        y = points[i, 1]
        b_gradient += 2 * ((w_current * x) + b_current - y)
        w_gradient += 2 * x * ((w_current * x) + b_current - y)
    b_gradient = b_gradient / N
    w_gradient = w_gradient / N
    new_b = b_current - (learningRate * b_gradient)
    new_w = w_current - (learningRate * w_gradient)
    return [new_b, new_w]

def gradient_descent_runner(points, starting_b, starting_w, learning_rate, num_iterations): # num_iteration 迭代次数
    b = starting_b
    w = starting_w
    for i in range(num_iterations):
        b, w = step_gradient(b, w, np.array(points), learning_rate)
    return [b, w]

def run():
    points = np.genfromtxt("data.txt", delimiter=",")
    learning_rate = 0.0001
    initial_b = random()
    initial_w = random()
    num_iterations = 1000
    print("Starting gradient descent at b = {0}, w = {1}, error = {2}"
          .format(initial_b, initial_w, 
                  compute_error_for_line_given_points(initial_b, initial_w, points)))
    print("Running...")
    [b, w] = gradient_descent_runner(points, initial_b, initial_w, learning_rate, num_iterations)
    print("After {0} iterations at b = {1}, w = {2}, error = {3}"
          .format(num_iterations, b, w, 
                  compute_error_for_line_given_points(b, w, points)))
run()

引用：https://blog.csdn.net/qq_37236745/article/details/103698507