[数据结构与算法]剑指offer day1(1.只出现一次的数字2.杨辉三角)

一、只出现一次的数字

（1）题目描述：
（2）解题思路：

由于在题目的说明中要求算法具有线性时间复杂度且不使用额外空间来实现，所以可以考虑通过位运算（这里用异或） 来实现。

异或运算的特点：
（1）一个数与0异或，异或的结果为这个数本身。
n ^ 0 = n; eg:101 ^ 000 = 101
（2）相同的数进行异或，异或结果为0。
n ^ n = 0; eg:101 ^101 = 000
（3）异或运算满足交换律。
a ^ b ^ c = a ^ c ^ b

根据以上解题思路，可以很快完成此题。

（3）程序代码：

class Solution 
{
public:
    int singleNumber(vector<int>& nums)
    {
        int value = 0;
        for(auto e :nums)
        {
            value ^= e;
        }
        return value;
    }
};

（4）运行截图：

二、杨辉三角

（1）题目描述：

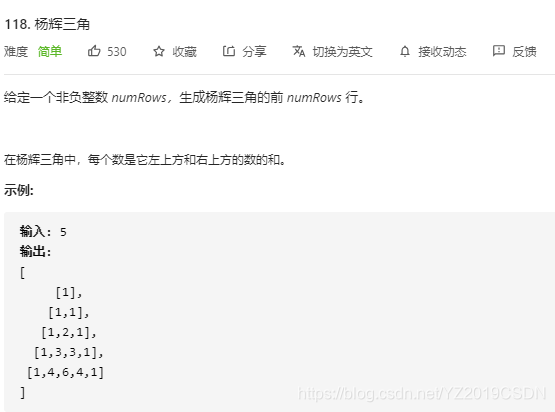
（2）解题思路：

要解决这个问题，最重要的是找出杨辉三角中的规律。

观察杨辉三角可以发现杨辉三角中每一行的第一个元素和最后一个元素都为1，其余元素为其上一行同列元素和前一列元素之和。在看出杨辉三角的这一特点之后，编程实现也就不难了。

（3）程序代码：

class Solution 
{
public:
    vector<vector<int>> generate(int numRows) 
    {
        vector<vector<int>> vv;
        vv.resize(numRows);
        for(size_t i = 1;i <= numRows;++i)
        {
            //初始化每一行的元素为0
            vv[i-1].resize(i,0);
            //每一行的第一个元素和最后一个元素为1
            vv[i-1][0] = 1;
            vv[i-1][i-1] = 1;
        }
        //其余元素为其上一行同列元素和前一列元素之和
        for(size_t i = 0;i < vv.size();++i)
        {
            for(size_t j = 0;j < vv[i].size();++j)
            {
                if(vv[i][j] == 0)
                {
                    vv[i][j] = vv[i-1][j-1] + vv[i-1][j];
                }
            }
        }
        return vv;
    }
};

（4）运行截图：

小编在每一道题的开始都给出了相应题目的链接，感兴趣的小伙伴可以自己动手做一做~