[数据结构与算法]数据结构绪论部分

绪论

什么是数据结构？

不同于计算机操作培训，注意与程序设计的区别。

Example 1

求n个数的最大值、次最大值。

//1.遍历 - 最朴素的方法
int main()
{
	int arr[10] = { 22,334,552,1,4,6,78,23,55,98 };
	int i = 0;
	int temp = 0;
	int max1 = arr[0];
	int max2 = arr[1];
	for (i = 1; i < 10; i++)
	{
		if (arr[i] > max1)
		{
			temp = max1;
			max1 = arr[i];
			arr[i] = temp;
		}
	}
	printf("%d\n", max1);
	for (i = 2; i < 10; i++)
	{
		if (arr[i] > max2)
		{
			temp = max2;
			max2 = arr[i];
			arr[i] = temp;
		}
	}
	printf("%d\n", max2); 
	return 0;
}

• 遍历方法共需进行$n?1+n?2=2n?3$次比较。

变题

有n个足球队比赛，问至少多少次比赛才能找到冠军和亚军。

解：
实际中通常采用锦标赛方法。（淘汰制）
设有8个数分别为5，7，3，6，8，9，4，2
两两为一组进行比较，大的胜出，小的淘汰。

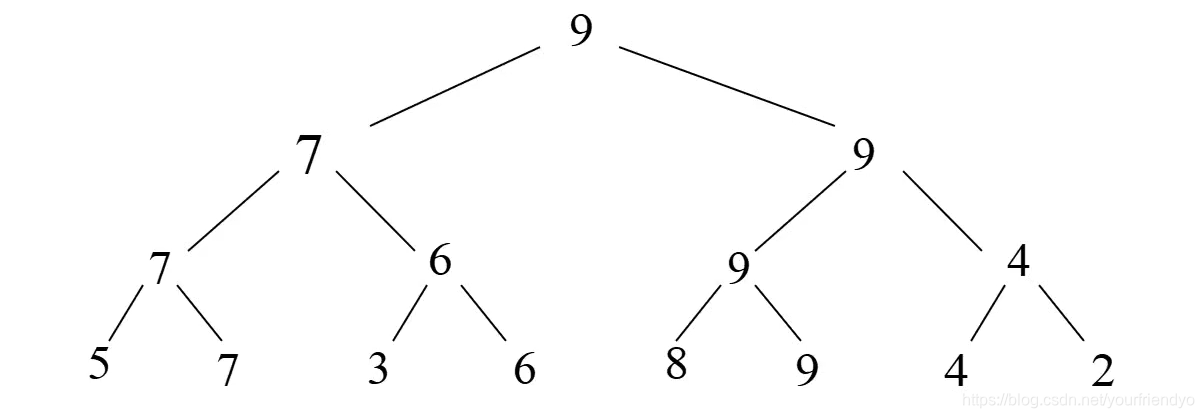
毋庸置疑的是，无论怎么分组，显然最大值永远不会被淘汰。故最大值为9。

共进行了$8/2+4/2+2/2=7$次比较。

1. 故变题寻找冠军的比较次数为$n/2+n/2^2+\dots +n/2^k=n?1$

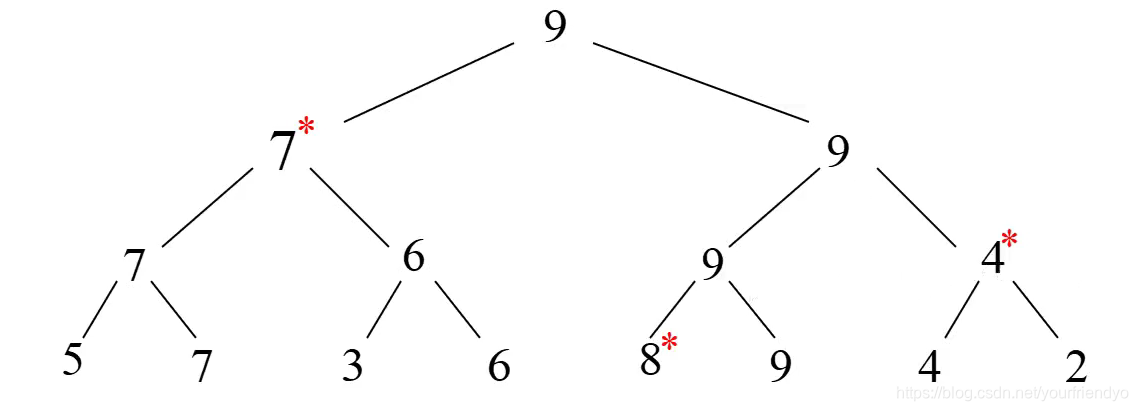
次最大值肯定是被最大值给比下去了，不然它就是最大值了。所以顺着这个思路，把所有和最大值进行过直接比较的数字跳出来，重新进行比较。

就是如图所示带*的数字，个数记为k，稍加思索则得出$k=lo{g}_{2}n$

2. 故变题寻找亚军的比较次数为$lo{g}_{2}n?1$

• 锦标赛方法共需$n?1+lo{g}_{2}n?1=n+lo{g}_{2}n?2$次比较。

课后思考：将该模型用C程序编写出来。

讨论

? 处理一般实际工程问题的方法。

1. 找出解决方案。
2. 找出最优解。（最节省资源：CPU和内存）

Example 2

判断表达式中括号是否匹配

$Z=((a+b)+c)?2+(3?5)/7?((6+2)/8+a)$

void match(char* ch)
{
	int count = 0;
	int i = 0; 
	while (ch[i]!= ';') 
	{
		if(ch[i] == '(')
			count++;
		else if (ch[i] ==')')
			count--; 
		i++;
	}
	if (count != 0)
		printf("%s\n","no match");
	else 
		printf("%s\n","match");
}

当然，上述代码是由左向右数括号数是否相等来判断括号是否匹配，很容易就可以举出反例 $f=)a+b($ ，所有该方法是不成熟的。

Example 3

交叉路口交通管理系统

1. 把可以走通的道路设为顶点
2. 如果两个顶点有冲突，用顶点之间的连线表示

变题 着色算法

• 在状态图中，相邻（有连线）的顶点不能是同一种状态。
• 故对于顶点的不同状态，我们用不同的颜色去表示。
• 由于四色定理，多余5叉的路口不能用少于4种颜色来表示。

在状态图中至少需要多少种颜色来表示？

Example 4

如何快速走出迷宫？

以上问题现阶段并不作要求，目的是向大家介绍下数据结构的研究问题。

现在我们是否能回答出刚开始时问大家的问题呢？数据结构是什么？

数据结构是研究的是非数值计算的程序设计方法。

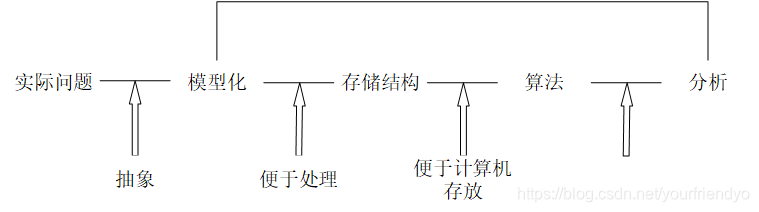
基本概念和术语

• 数据（data）——能输入到计算机并能被计算机程序处理的符号的总称
  • 非常广泛的概念，一般我们讨论的都是数据。
• 数据元素（data element）——数据的基本单位（例如整型数，字符串，结构等）
  • 数据的基本单位，不可再分。
• 数据对象（data object）——性质相同的数据元素的集合
  • 是一个集合，比如说班上的所有学生。
• 数据结构（data structure）——是相互之间存在一种或多种特定关系的数据元素的集合
  • 数据结构分成两块，一是数据，二是结构，所谓结构即相互关系。

 数据结构是一门描述计算机处理对象和它们之间的关系以及相应的处理方法的学科。

（数据对象、数据关系、基本操作）