题目描述
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
方法一:单调栈
雨水存在的地方是低洼的地方,维护一个单调栈,栈内存储的元素是数组的下标,如果遍历到的元素值 height[i] 大于栈顶元素,那么此时可以形成一个低洼的地方,因此需要计算该低洼的地方的高和宽。首先删除栈顶元素。
- 高度:可以承接雨水的左右两个柱子的此时height[i] 与 新的栈顶元素之间的最小值,然后减去删除的栈顶元素所对应的高度值。为啥要减去栈顶元素对应的高度值呢?每次求解加的是一个横向的矩形,可以结合[4,6]区间的雨水计算方法理解。
- 宽度是当前下标元素减去新的栈顶元素然后减去1,表示当前柱子 i (右边界)与左边柱子(左边界)之间的距离。
- 时间复杂度和空间复杂度都为O(n)
class Solution {
public:
int trap(vector<int>& height) {
int n=height.size();
stack<int> stk;
int res=0;
for(int i=0;i<n;i++)
{
while(!stk.empty()&&height[stk.top()]<height[i])
{
int t=stk.top();
stk.pop();
if(!stk.empty())
{
int h=min(height[i],height[stk.top()])-height[t];
int w=i-stk.top()-1;
res+=h*w;
}
}
stk.push(i);
}
return res;
}
};
方法二:动态规划
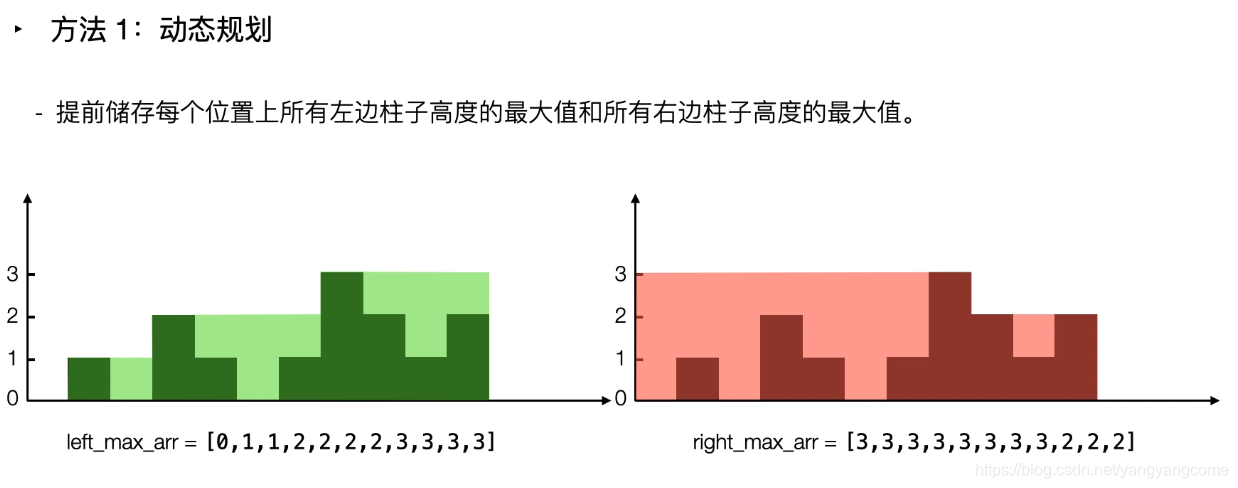
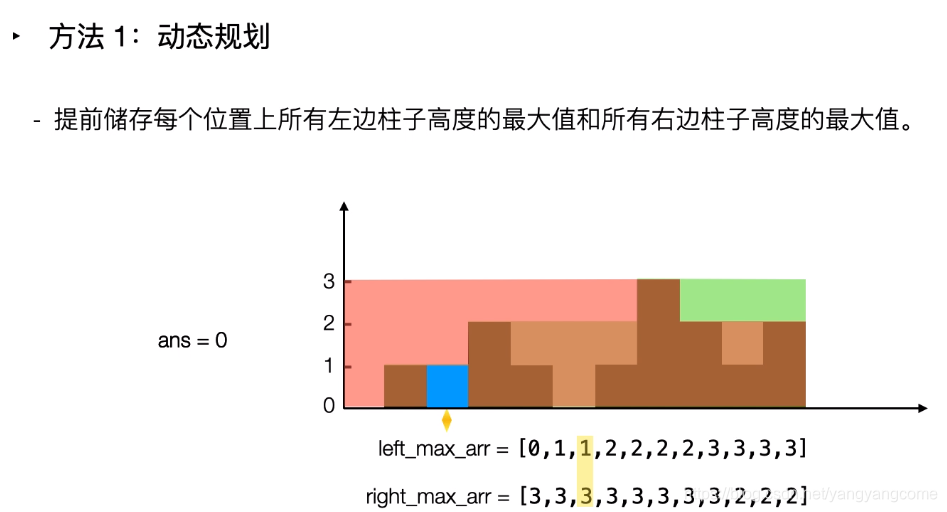
如图所示,从左向右找到该位置 i 处左边最大的值,从右往左找到位置 i 处右边最大的值,求解雨水的过程如第二张图所示,在left_max和right_max中取最小值然后减去当前位置的height[i] 即可。
class Solution {
public:
int trap(vector<int>& height) {
int n=height.size();
if(!n) return 0;
int res=0;
vector<int> left(n,0); left[0]=height[0];
vector<int> right(n,0); right[n-1]=height[n-1];
for(int i=1;i<n;i++)
{
left[i]=max(height[i],left[i-1]);
}
for(int i=n-2;i>=0;i--)
{
right[i]=max(height[i],right[i+1]);
}
for(int i=0;i<n;i++)
{
res+=min(left[i],right[i])-height[i];
}
return res;
}
};
方法三:双指针
动态规划是将位置 i 处左右两边的最大值保存在了数组中,现在可以使用双指针减少了空间复杂度,使用leftmax保存位置left处的左边最大值,使用rightmax保存位置right处右边的最大值,以左指针为例,如果该位置处的值大于leftmax,那么更新leftmax,否则会形成一个低洼的地段,此时可以计算雨水的面积了,计算面积的时候是按照一列一列来计算的,因此只需要考虑高度即可,因此是leftmax-height[left],之后left向右移动。右指针类似。
可以看到双指针与动态规划方式本质上是类似的,都是寻找位置 i 处的左边最大值和右边最大值,只不过省去了取min的操作,原因在于如果height[left]<height[right]那么要更新leftmax和rightmax时,leftmax肯定小于rightmax,因此只需要在leftmax这边操作即可,相当于动态规划中的min(left[i],right[i])操作。
class Solution {
public:
int trap(vector<int>& height) {
int left=0,right=height.size()-1;
int res=0;
int leftmax=0,rightmax=0;
while(left<right)
{
if(height[left]<height[right])
{
if(height[left]>leftmax) leftmax=height[left];
else res+=leftmax-height[left];
left++;
}
else
{
if(height[right]>rightmax) rightmax=height[right];
else res+=rightmax-height[right];
right--;
}
}
return res;
}
};