图书系统推荐算法——矩阵分解
文章目录
前言
近期找实习,某家公司要我做的关于推荐算法的笔试题,第一次接触推荐算法,花了一些时间学习了一下,将内容保存一下,留个记录。
一、数据来源与相关介绍
1.1 数据来源与说明
本答卷的数据来源于:
http://www2.informatik.uni-freiburg.de/~cziegler/BX/
由于该数据的Excel与CSV格式的文件存在大量内容错位与格式错误,本文选取了数据库脚本文件,利用Python进行转换。

1.2 数据简介
Book Crossing 是一个书籍推荐系统数据,用以向用户推荐偏好的书籍。 由Cai-Nicolas Ziegler在经过4周的爬网(2004年8月/ 2004年)中,在人类系统 首席技术官Ron Hornbaker的允许下,从Book-Crossing社区中收集。包含278,858个用户(匿名但具有人口统计信息),提供1,149,780个评分(显式/隐式),约271,379本书。数据集中包含三张表,分别BX用户表,BX书表,BX书评表。
属性信息如下:
①BX用户表
a)UserID 用户id
b)Location 位置
c)Age 年龄
②BX书
a)ISBN ISBN标识
b)BookTitle 书名
c)BookAuthor 书作者
d)Year-Of-Publication 出版年
e)Publisher 发布者
f)ImageURLS
h)ImageURLM
i)ImageURLL
③BX书评
包含书评信息。等级(Book-Rating)是显式的,以1-10(较高的值表示较高的欣赏度)表示,或隐式的,以0表示。
a)UserID 用户id
b)ISBN ISBN标识
d)BookRating 等级
1.3 数据选取
根据各数据表中包含的数据标签,可以看出搭建推荐系统需要用到UserID (用户id)、ISBNISBN (标识)、BookRating (等级)、BookTitle(书名)等几个标签的内容。
二、数据基础分析
本文对三个数据内容作基础分析,即“同一用户参与评论数”、“同一书籍被评论数”以及“用户评分”。
2.1 同一用户参与评论数的基础分析
下图展示了关于同一用户参与评论数的一些统计结果,可以发现用户评论众数、中位数为1,表明超过50%的用户只阅读了一本书(可能未对阅读书籍进行打分,即评价为0)。评论数最大值为13602,试想一下,一个人阅读了13602本数,其可能是只是刷阅读数据的读者或者从事阅读工作的书籍评论人员。
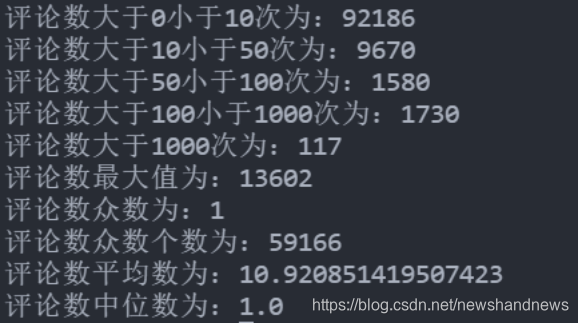
下图是阅读评论数的箱线图,在绘图时对数据进行了一下修改,由于数值较为分散且跨度较大,在作箱线图时对数值进行了取对数以便进行绘图。箱线图可以很好的展示上文的统计结果。
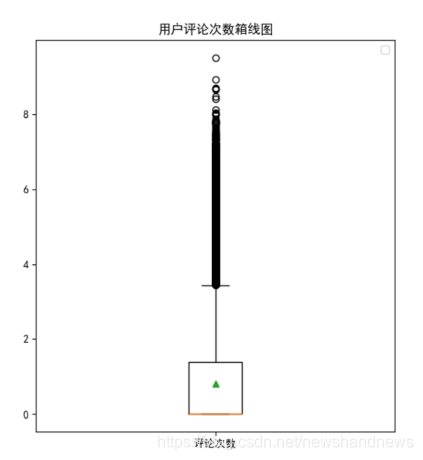
为了便于知道同一用户评论数在不同层次的占比,画出各个层次的饼图并对其比例进行标注。从图中可以看出,评论数小于10次的用户占了记录总用户的87.6%,评论数大于10小于50次的用户占了记录总用户的9.2%,评论数大于50小于100次的用户占了记录总用户的1.5%,评论数大于100小于1000次的用户占了记录总用户的1.6%,评论数大于1000次的用户仅占了记录总用户0.1%。显然绝大部分用户阅读量都在50本书籍以下。
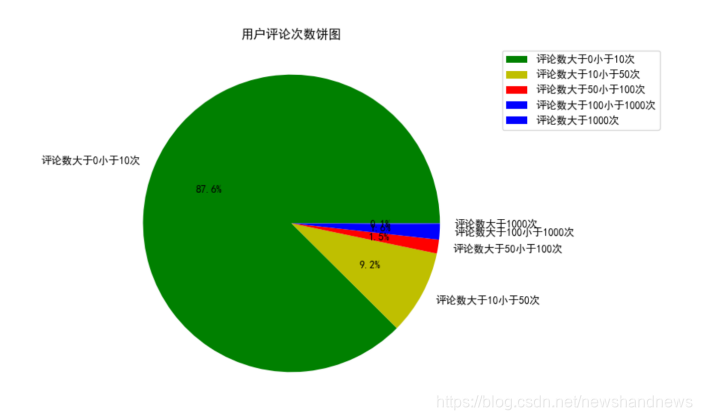
2.2 同一书籍被评论数的基础分析
下图展示了书籍被评论数的一些统计结果,同上文分析一样,书籍被评论数众数和中位数也都为1,即超过一半的书籍仅被1名用户阅读,可以被认为是无太多价值的书籍。书籍被评价次数最多的为2502次,考虑到被评价次数超过1000的书籍仅为2本,所以其受欢迎度相当高。
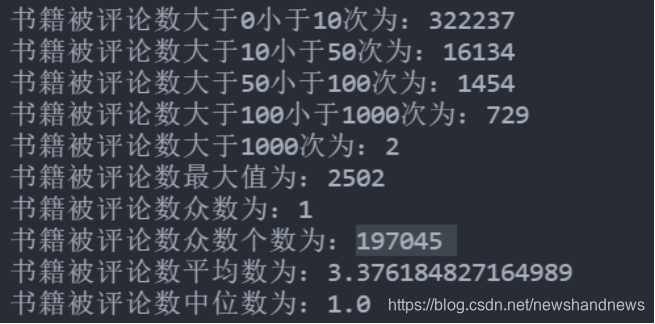
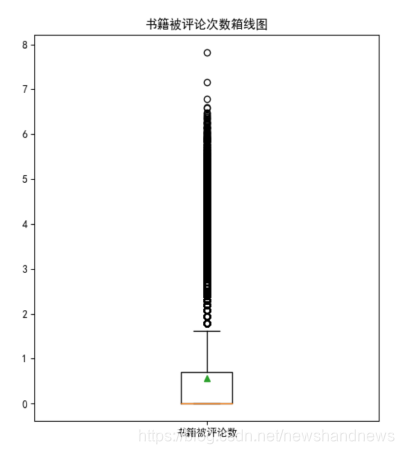
下图是书籍被评论数的箱线图,同上文一样,在绘图时对数据进行了一下修改,由于数值较为分散且跨度较大,在作箱线图时对数值进行了取对数以便进行绘图。箱线图也很好的展示上文的统计结果。
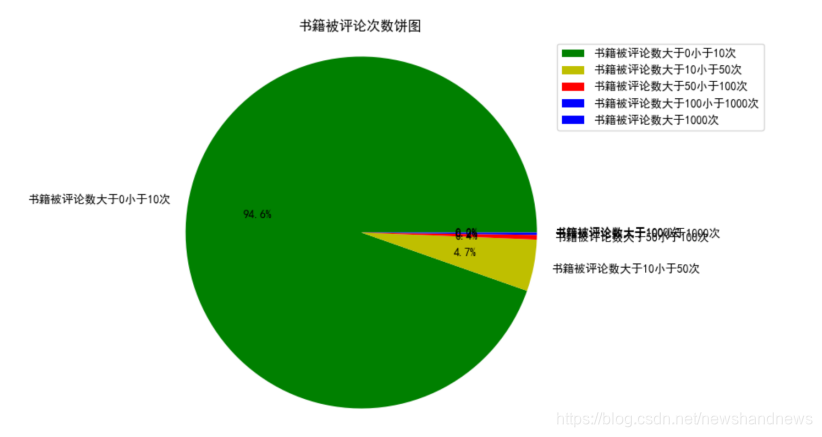
同样的,为了便于知道同一书籍被评论数在不同层次的占比,画出各个层次的饼图并对其比例进行标注。从图中可以看出,书籍被评论数小于10次的书籍占了记录总书籍的94.6%,书籍被评论数大于10小于50次的书籍占了记录总书籍的4.7%,书籍被评论数大于50小于100次的书籍占了记录总书籍的0.4%,书籍被评论数大于100小于1000次的书籍占了记录总书籍的0.2%,书籍被评论数大于1000次的书籍仅为2本,仅占了记录总书籍0.1%。显然绝大部分用户阅读量都在50本书籍以下。
2.3 评分数据基础分析
对用户的打分的具体分值作具体分析,发现隐性打分(即评价分值为0)的情况占据了绝大部分。打低分的数量明显比打高分的少的多。
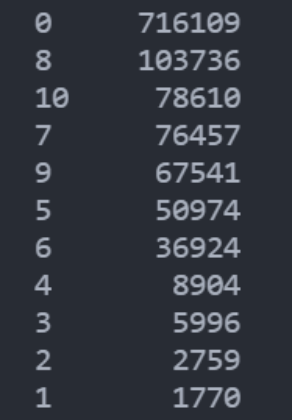
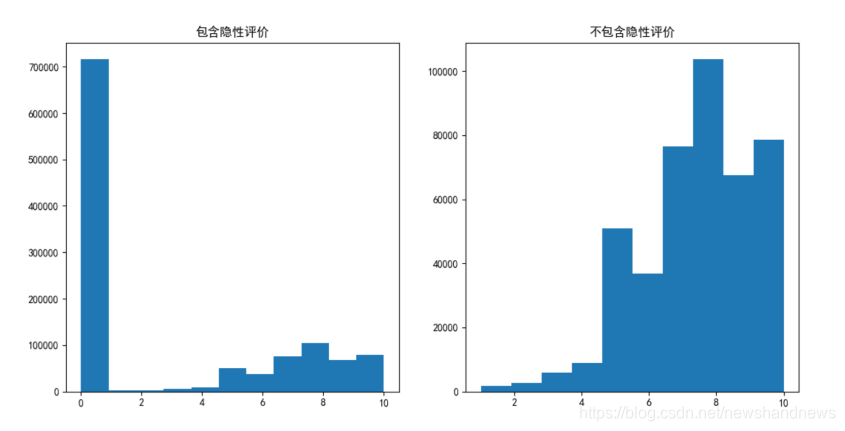
为了更形象的表现出评分的情况,对评分数据作直方图。其中左图包含隐性打分,其更形象的展现了读者对于书籍进行评价行为即大部分读者不会显性的对书籍进行评价。右图不包含隐性评价,可以看出对书籍喜欢(大于等于7分)的评价明显比不喜欢(小于等于4分)数量多得多;其中,打8分的最多。
三、推荐算法的设计
3.1 基于书籍受欢迎程度进行设计
首先从书籍的受欢迎程度来对哪些新加入的读者或者在当前时间点阅读书籍较少的读者进行推荐,这些读者由于历史数据的匮乏,无法直接根据其偏好进行书籍推荐,故采用这种方法进行推荐。
从书籍被阅读的次数进行受欢迎程度的度量,下表展示了数据中被评分最多的10本书籍。
| ISBN | 书籍被评论次数 |
|---|---|
| 0971880107 | 2502 |
| 0316666343 | 1295 |
| 0385504209 | 883 |
| 0060928336 | 732 |
| 0312195516 | 723 |
| 044023722X | 647 |
| 0679781587 | 639 |
| 0142001740 | 615 |
| 067976402X | 614 |
| 0671027360 | 586 |
下图根据书籍被评论数的多少以及书籍的“TSBN”号对书名及作者进行查询后得到的。其选取了被阅读最多的可查询的10本书作为对相关对象的推荐

3.2 基于矩阵分解的推荐算法
由于条件的限制,为了加快模型的运转速度,本文对原始数据进行了选取。选择对超过100本书籍进行打分的用户以及其中被超过100名用户打分的书籍。为了增多用户的评分数据,考虑到大多数读者都对书籍进行了积极评价,且对书籍打6分的数量明显偏少,故将读者的隐性评价全部设为6分。在此基础上,导出读者-书籍评分矩阵。矩阵的相关信息如图所示。
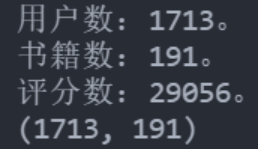
从图可知,本文所用的评分矩阵的形状为(173,191),即包含了1713名读者以对191本书籍进行打分的情况。在评分矩阵中,包含了29056的评分的具体分值,通过计算还有298127个缺失值,矩阵高度稀疏。
本文所用数据数读者-书籍评分矩阵,可以采用矩阵分解预测出评分矩阵中的缺失值,基于算法结果对相关用户进行书籍推荐。下表为在不同参数情况下矩阵分解算法的函数损失值的情况。从表中可以明显看出,k值的选取对模型精度有显著影响。
在几种试验的结果中,在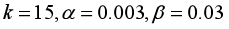
的情况下,所得模型的结果最好,此时函数的损失值为17429。可以发现,损失值依然很大,但是需要知道的是,该值是29056个评分的损失的和,去除掉转换隐性评分的影响,在现有条件下该值是可以接受的。
| 序号 | alpha | beta | k | 迭代次数 | 损失函数值 |
|---|---|---|---|---|---|
| 1 | 0.008 | 0.08 | 2 | 500 | 49821 |
| 2 | 0.008 | 0.08 | 5 | 500 | 42798 |
| 3 | 0.005 | 0.05 | 10 | 1500 | 26857 |
| 4 | 0.003 | 0.03 | 15 | 1600 | 17429 |
| 5 | 0.005 | 0.05 | 40 | 1000 | 18249 |
本文选取最后一次试验的参数值即对相关用户进行推荐。随着迭代次数的增加,各迭代次数下函数损失值为:
第10次迭代的损失值为:56239.51。
第20次迭代的损失值为:49932.92。
第30次迭代的损失值为:46338.80。
第40次迭代的损失值为:43726.73。
……
第950次迭代的损失值为:18314.19。
第960次迭代的损失值为:18300.63。
第970次迭代的损失值为:18287.35。
第980次迭代的损失值为:18274.34。
第990次迭代的损失值为:18261.59。
第1000次迭代的损失值为:18249.09。
其迭代次数变换图如图所示。
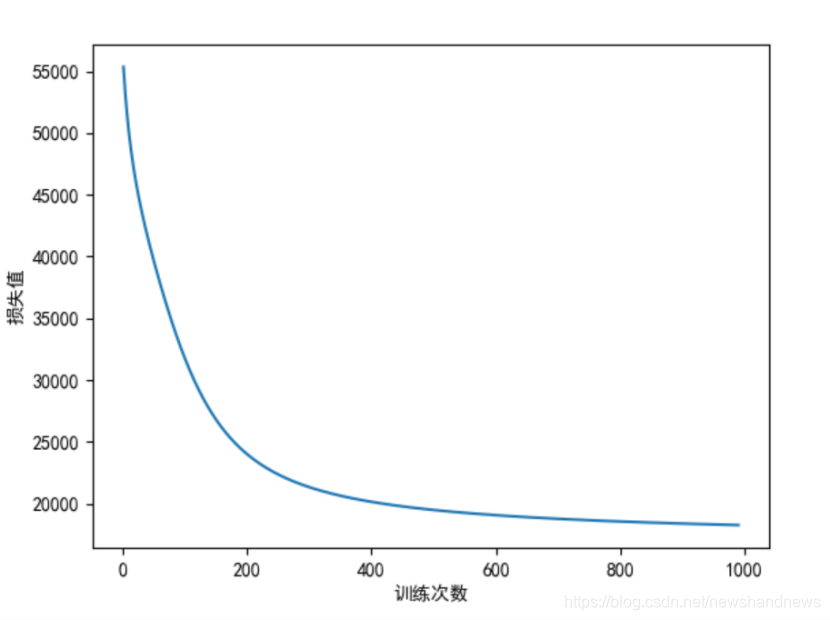
从图中可以看出,损失函数值随着迭代次数的增加不断收敛。由于条件限制,迭代此数无法增加,否则应该能够得到更加精确的拟合结果。
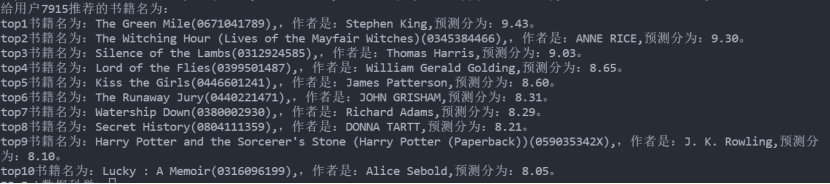
选取两名用户,根据拟合结果对其进行推荐,每人推荐10本书籍,推荐结果如图所示。
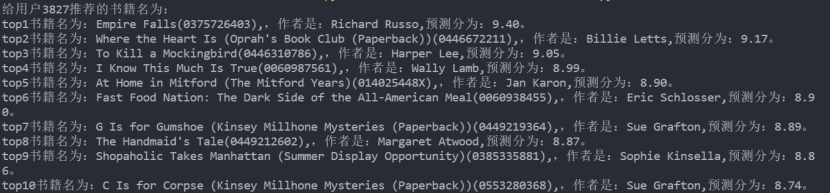
四、总结
在做题中遇到了很多问题:
1)下载下来CSV格式的数据出现了乱码并且数据有很多缺失,表格中的数据大多都在一个单元格内。权衡之下选择了不熟悉的sql脚本数据,利用Python将其转换成了Excel表格,之间遇到很多问题。包括数据库语言的与插入数据格式的无法读取等问题,花费了较长时间。
2)评分矩阵用户和书籍的选取也经过了多次修改,本来准备选取读取超过10本和被评价超过10本的数据进行构建评分矩阵,但是后来发现数据量太大电脑计算实践太长而无奈改成100。
3)由于之前只在机器学习的学习中接触过矩阵分解——非负矩阵分解进行数据降维,关于MF算法没有接触,故花了不少时间去了解矩阵分解。在实际操作中,由于电脑性能的影响,算法迭代花去了较长时间,其中还用几次电脑卡死,让本来还想做一个协同过滤的我猝不及防,最终无奈放弃。
通过本次做题,有了如下的收获:
1)对数据库语言有了一定的了解。
2)强化了运用Numpy库,pandas库,matplotlib库的能力。
3)对推荐算法有了初步的了解,今后有机会计划尝试逻辑回归,深度学习在推荐算法上的应用。
四、附录
附上做题中一些重要算法的代码实现
import pandas as pd
import sqlite3
from matplotlib import pyplot as plt
import numpy as np
# 字体问题
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def sql_to_excel(query, sql_file, encoding, n, select, columns):
"""将sql后缀文件数据转换为excel表
输入
query:创建数据表语句
sql_file:sql后缀文件路径
encoding:编码格式
n:遍历起始位置
select:查询语句
columns:列标签
输出:
data数据
"""
con = sqlite3.connect(':memory:')
con.execute(query)
con.commit()
with open(sql_file,encoding=encoding,mode='r') as f:
# 读取整个sql文件,以分号切割。[:-1]删除最后一个元素,也就是空字符串
sql_list = f.read().split('\n')[n:-1]
i = 0
for x in sql_list:
i += 1
# 判断包含空行的
if '\n' in x:
# 替换空行为1个空格
x = x.replace('\n', ' ')
# 判断多个空格时
if ' ' in x:
# 替换为空
x = x.replace(' ', '')
# 处理BX-Book文件时的附加条件
# x = x.replace("\'","*")
# x = x.replace(',*', ",'")
# x = x.replace('*,', "',")
# x = x.replace('(*', "('")
# x = x.replace('*)', "')")
sql_item = x
# print(sql_item, i)
con.execute(sql_item)
con.commit()
# 查询并将数据转为DateFrame格式
cursor = con.execute(select)
rows = cursor.fetchall()
data = pd.DataFrame(rows, columns=columns)
return data
矩阵分解及推荐的实现:
import pandas as pd
from matplotlib import pyplot as plt
import numpy as np
# 字体问题
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def MF(data, k, alpha, beta, maxsteps):
"""矩阵分解的实现:
输入:
data:评分矩阵
k:矩阵分量的中间维度
alpha:学习步长
beta: 正则化参数
maxsteps:最大迭代次数
输出:
p:用户关系矩阵
q:产品关系矩阵的转置矩阵
loss:损失函数值
result: 损失函数值容器
"""
m, n = data.shape
p = np.random.random((m, k))
q = np.random.random((k, n))
result = []
for t in range(maxsteps):
# print(t)
for i in range(m):
for j in range(n):
if data[i,j]:
error = data[i][j] - np.dot(p[i,:], q[:,j])
for r in range(k):
p[i][r] += alpha * (2 * error * q[r][j] - beta * p[i][r])
q[r][j] += alpha * (2 * error * p[i][r] - beta * q[r][j])
loss = 0
for i in range(m):
for j in range(n):
if data[i,j]:
error = data[i][j] - np.dot(p[i,:], q[:,j])
loss += pow(error, 2)
for r in range(k):
loss += (beta/2) * (pow(p[i][r], 2) + pow(q[r][j], 2))
result.append(loss)
if (t+1) % 10 == 0:
print('第{}次迭代的损失值为:{:.2f}。'.format(t+1, loss))
if loss < 0.001:
break
return p, q, loss, result
def get_list_max_index(list_, n):
"""输出列表中最大的前n个数的索引
输入:
list:列表
n:需要输出的数目
输出:
最大的前n个数的索引列表
"""
N_large = pd.DataFrame({'score': list_}).sort_values(by='score', ascending=[False])
return list(N_large.index)[:n]
def recommend_information(data, new_MF, bxbooks, sort_user_rating, i, nums):
"""输出推荐书籍
输入:
data:原始评分矩阵
new_MF: 预测频分矩阵
bxbook: 书籍信息表
sort_user_rating:分数排名索引
i: 用户在矩阵中的下标
nums: 推荐书籍的本数
输出:
无
"""
num = 0
for k in sort_user_rating:
# print(data.values[i,k])
if data.values[i,k]:
continue
if data.columns[k] in bxbooks.index:
# print(data.columns[k])
num += 1
if num > nums:
break
book = bxbooks.loc[data.columns[k],'BookTitle'].replace("\*", "'")
book = book.replace("#", "'")
information = 'top{}'.format(num) + '书籍名为:{}'.format(book)
information = information + '({}),'.format(data.columns[k])
information = information + ',作者是:{},'.format(bxbooks.loc[data.columns[k],'BookAuthor'])
information = information + '预测分为:{:.2f}。'.format(new_MF.iloc[i,k])
print(information)
def select(data, new_MF, bxbooks, user, m, n, nums):
"""选择推荐书籍
输入:
data:原始评分矩阵
new_MF: 预测频分矩阵
bxbook: 书籍信息表
user:需要推荐用户名列表
i: 用户在矩阵中的下标
nums: 推荐书籍的本数
输出:
无
"""
user_index = data.index
for j in user:
print('给用户{}推荐的书籍名为:'.format(j))
i = list(user_index).index(j)
user_rating = new_MF.iloc[i,:].values
sort_user_rating = get_list_max_index(list(user_rating), n)
recommend_information(data, new_MF, bxbooks, sort_user_rating, i, nums)
def topN(path, new_path, bxbooks_path, user, nums):
"""推荐书籍
输入:
path:原始评分矩阵路径
new_path: 预测频分矩阵路径
bxbooks_path: 书籍信息表路径
user:需要推荐用户名列表
nums: 推荐书籍的本数
输出:
无
"""
data = pd.read_excel(path, index_col=0).replace(np.nan, 0)
new_MF = pd.read_excel(new_path, sheet_name='new', header=None)
bxbooks = pd.read_excel(bxbooks_path, index_col=0)
m, n = data.shape
select(data, new_MF, bxbooks, user, m, n, nums)