[数据结构与算法]Task2回归问题

1、线性回归假设数据集中特征与结果存在着线性关系；

　　等式：y = mx + c

　　y为结果，x为特征，m为系数，c为误差，在数学中m为梯度c为截距

这个等式为我们假设的，我们需要找到m、c使得mx+c得到的结果与真实的y误差最小，这里使用平方差来衡量估计值与真实值得误差（如果只用差值就可能会存在负数）； 用于计算真实值与预测值的误差的函数称为：平方损失函数（squard loss function）；这里用L表示损失函数，所以有：

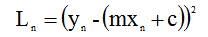
　　整个数据集上的平均损失为：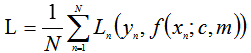

　　我们要求得最匹配的m与c使得L最小；
数学表达式可以表示为：

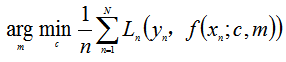
2、在线性回归模型中，最小二乘估计等于噪声的极大似然估计

3、多项式回归中，当阶数太高时边缘的置信区间会很大，所以一般不超过4阶

4、树模型能很好的解决缺失值和异常值，线性模型无法解决；但是树模型的预测准确性会差一些

5、有时原问题很难，但是在对偶问题上就会简单，任何一个原问题变成对偶问题时都会变成一个凸优化问题

6、线性拟合-使用numpy

import numpy as np
X=[ 1 ,2  ,3 ,4 ,5 ,6]
Y=[ 2.51 ,3.52 ,4.48 ,5.51 ,6.47 ,7.51]
z1 = np.polyfit(X, Y, 1)  #一次多项式拟合，相当于线性拟合
p1 = np.poly1d(z1)
print (z1)  #[0.99657143 1.512     ]
print (p1)  # 0.9966 x + 1.512

得到线性函数模型