2021.7.16模拟赛C组总结

这次比赛，题虽然不难，但丝毫不影响我打挂…唉…

在这里插入图片描述

0+100+50+0=150

题解

T1

题目描述：

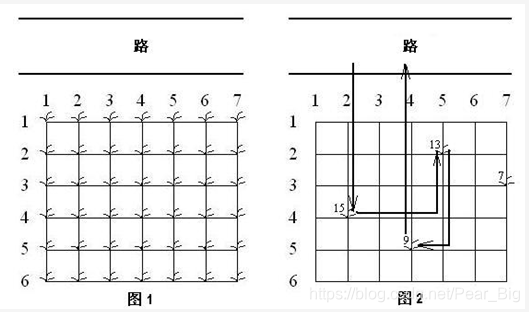
? 鲁宾逊先生有一只宠物猴，名叫多多。这天，他们两个正沿着乡间小路散步，突然发现路边的告示牌上贴着一张小小的纸条：“欢迎免费品尝我种的花生！”。鲁宾逊先生和多多都很开心，因为花生正是他们的最爱。在告示牌背后，路边真的有一块花生田，花生植株整齐地排列成矩形网格（如图1）。

? 有经验的多多一眼就能看出，每棵花生植株下的花生有多少。为了训练多多的算术，鲁宾逊先生说：“你先找出花生最多的植株，去采摘它的花生；然后再找出剩下的植株里花生最多的，去采摘它的花生；依此类推，不过你一定要在我限定的时间内回到路边。”

在这里插入图片描述

我们假定多多在每个单位时间内，可以做下列四件事情中的一件：
(1) 从路边跳到最靠近路边（即第一行）的某棵花生植株；
(2) 从一棵植株跳到前后左右与之相邻的另一棵植株；
(3) 采摘一棵植株下的花生；
(4)从最靠近路边（即第一行）的某棵花生植株跳回路边。

现在给定一块花生田的大小和花生的分布，请问在限定时间内，多多最多可以采到多少个花生？注意可能只有部分植株下面长有花生，假设这些植株下的花生个数各不相同。例如在图2所示的花生田里，只有位于(2, 5), (3, 7), (4, 2), (5, 4)的植株下长有花生，个数分别为13, 7, 15, 9。沿着图示的路线，多多在21个单位时间内，最多可以采到37个花生。

比赛思路：

? 思路？不存在的，当时去打后面的题了，结果后面用太长时间了，~~我没看到鲁宾逊说的话~~

正解：

? 由于每次都是去花生最多的，所以用结构体pt[i].x,pt[i].y,pt[i].sum分别表示第i棵有花生的地方的x,y坐标和花生数，然后以花生数为关键字进行从大到小排序，最后按顺序读入，进行判断时间，当时间不足以去下一棵花生采摘并返回时，直接输出answer

Tips:

设
$range(x_A,y_A,x_B,y_B)$
为网格图中点A至点B的曼哈顿距离,则
$range(x_A,y_A,x_B,y_B)=|x_A-x_B|+|y_A-y_B|$
Code:

#include<bits/stdc++.h>
#define in scanf
#define out printf
#define rint register int
using namespace std;
const int N=2001;
int n,m,t,s,a[N][N];
struct track {
	int x;
	int y;
	int sum;
};
track pt[N*N];//存储花生
int abs(int x)
	{return x>0?x:-x;}
void swp(track&a,track&b) {
	track t=a;
	a=b;b=t;
	return;
}
int main() {
	in("%d%d%d",&n,&m,&t);
	for(rint i=1;i<=n;i++)
		for(rint j=1;j<=m;j++) {
			in("%d",&a[i][j]);
			if(a[i][j]!=0) {
				s++;
				pt[s].x=i;
				pt[s].y=j;
				pt[s].sum=a[i][j];
			}
		}//读入
	for(rint i=1;i<s;i++)
		for(int j=i+1;j<=s;j++)
			if(pt[i].sum<pt[j].sum) swp(pt[i],pt[j]);//排序(数据小可用冒泡排序)
	pt[0].y=pt[1].y;//初始化
	int ans=0,tim=0;
	for(rint i=1;i<=s;i++) {
		tim=tim+(abs(pt[i].x-pt[i-1].x)+abs(pt[i].y-pt[i-1].y)+1);//计算时间
		if(tim+pt[i].x>t) {//判断是否还能继续摘
			out("%d",ans);
			return 0;
		}
		else ans+=pt[i].sum;//统计花生数
	}
	out("%d",ans);
	return 0;
}

T2

题目描述：

? 我们可以把由“0”和“1”组成的字符串分为三类：全“0”串称为B串，全“1”串称为I串，既含“0”又含“1”的串则称为F串。

? FBI树是一种二叉树，它的结点类型也包括F结点，B结点和I结点三种。由一个长度为2N的“01”串S可以构造出一棵FBI树T，递归的构造方法如下：

T的根结点为R，其类型与串S的类型相同；
若串S的长度大于1，将串S从中间分开，分为等长的左右子串S1和S2；由左子串S1构造R的左子树T1，由右子串S2构造R的右子树T2。

现在给定一个长度为2N的“01”串，请用上述构造方法构造出一棵FBI树，并输出它的后序遍历序列。

[1]二叉树：二叉树是结点的有限集合，这个集合或为空集，或由一个根结点和两棵不相交的二叉树组成。这两棵不相交的二叉树分别称为这个根结点的左子树和右子树。

[2]后序遍历：后序遍历是深度优先遍历二叉树的一种方法，它的递归定义是：先后序遍历左子树，再后序遍历右子树，最后访问根。

比赛思路：

? 直接建一棵线段树，每个节点表示它所表示的区间情况，如果它的子节点不相同或存在"F"，那么它就是"F"，否则就为两个子节点共同表示的字母，最后递归遍历即可。

正解：

? 做法太多了，没理解错题意就能AC

Code:

#include<bits/stdc++.h>
#define in scanf
#define out printf
#define rint register int
#define ls i+i
#define rs i+i+1
const int d[11]={1,2,4,8,16,32,64,128,256,512,1024};
const int N=1025;
int n,a[N],tre[N*8],b;
char s[N];
bool bz[N*8];
void build(int left,int right,int i) {//建树
	if(left==right) {
		tre[i]=a[left];
		return;
	}
	int middle=left+right>>1;
	build(left,middle,ls);
	build(middle+1,right,rs);
	if(tre[ls]==0 or tre[rs]==0) return;//如果为叶节点就跳过
	if(tre[ls]==3 or tre[rs]==3 or tre[ls]!=tre[rs]) {
		tre[i]=3;
		return;
	}
	else if(tre[ls]==1) {
		tre[i]=1;
		return;
	}
	else tre[i]=2;
	return;
}
void treeout(int i) {//递归遍历
	if(bz[ls]==false) treeout(ls);
	if(bz[rs]==false) treeout(rs);
	if(tre[i]==1) out("I");
	if(tre[i]==2) out("B");
	if(tre[i]==3) out("F");
	bz[i]=true;//标记
	return;
}
int main() {
	in("%d",&n);
	in("%s",s+1);
	for(rint i=1;i<=d[n];i++)
		if(s[i]=='1') a[i]=1;
			else a[i]=2;
	build(1,d[n],1);
	for(rint i=d[n];i<=2*d[n];i++)
		bz[ls]=bz[rs]=true;
	treeout(1);
	return 0;
}

T3

题目描述：

? 人类终于登上了火星的土地并且见到了神秘的火星人。人类和火星人都无法理解对方的语言，但是我们的科学家发明了一种用数字交流的方法。这种交流方法是这样的，首先，火星人把一个非常大的数字告诉人类科学家，科学家破解这个数字的含义后，再把一个很小的数字加到这个大数上面，把结果告诉火星人，作为人类的回答。火星人用一种非常简单的方式来表示数字——掰手指。火星人只有一只手，但这只手上有成千上万的手指，这些手指排成一列，分别编号为1，2，3……。火星人的任意两根手指都能随意交换位置，他们就是通过这方法计数的。一个火星人用一个人类的手演示了如何用手指计数。如果把五根手指——拇指、食指、中指、无名指和小指分别编号为1，2，3，4和5，当它们按正常顺序排列时，形成了5位数12345，当你交换无名指和小指的位置时，会形成5位数12354，当你把五个手指的顺序完全颠倒时，会形成54321，在所有能够形成的120个5位数中，12345最小，它表示1；12354第二小，它表示2；54321最大，它表示120。下表展示了只有3根手指时能够形成的6个3位数和它们代表的数字：三进制数 123 132 213 231 312 321 代表的数字 1 2 3 4 5 6 现在你有幸成为了第一个和火星人交流的地球人。一个火星人会让你看他的手指，科学家会告诉你要加上去的很小的数。你的任务是，把火星人用手指表示的数与科学家告诉你的数相加，并根据相加的结果改变火星人手指的排列顺序。输入数据保证这个结果不会超出火星人手指能表示的范围。

比赛思路：

? 想过康托展开，可是不会逆康托，写暴力TLE50

正解：

? 康托展开+逆康托

Code:等我

T3

题目描述：

在这里插入图片描述

比赛思路：

? 纯暴力高精度，试过推公式求位数然后只计算后500位，结果失败，没想到出题人一分也没给~~纯粹因为我太暴力了~~

正解：

? 用快速幂或压位配合高精度运算，只算后500位，然后用公式求len，公式：
$2的n次幂下的十进制位数=?n/log_2(10)?+1$
Code:数据并不是极大的，我用了个神奇的优化，实现更简单我懒

#include<bits/stdc++.h>
#define in scanf
#define out printf
using namespace std;
const unsigned long long T=(long long)1<<60;//乘数
const int N=600;
unsigned long long t,m,a[N]={0,1};
int main() {
	in("%d",&t);
	unsigned long long len=1;
	for(int i=1;i<=t/60;i++) {
		unsigned long long jw=0;
		while(len<=500) {
			a[len]=a[len]*T+jw;//一次乘2的60次方，优化时间复杂度
			jw=a[len]/10;
			a[len]%=10;
			len++;
		}
		len=1;
	}
	for(unsigned long long i=1;i<=t%60;i++) {//乘完剩下的
		unsigned long long jw=0;
		while(len<=500) {
			a[len]=a[len]*2+jw;
			jw=a[len]/10;
			a[len]%=10;
			len++;
		}
		len=1;
	}
	m=(t/log2(10))+1;
	out("%d\n",m);
	for(unsigned long long i=500;i>=2;i--)
		out("%d",a[i]);
	out("%d",a[1]-1);
	return 0;
}