[POI2010]GIL-Guilds
比较显然。只要我们保证对于每一个节点都是由颜色不同的点转移过来即可。只需进行一次 dfs ,时间复杂度 O(n) 。
[POI2005]SKA-Piggy Banks
不难发现每个点都有且仅有一个出边,所以这个图只能是若干个 环+单链 组成。用并查集数一下联通块个数即可。
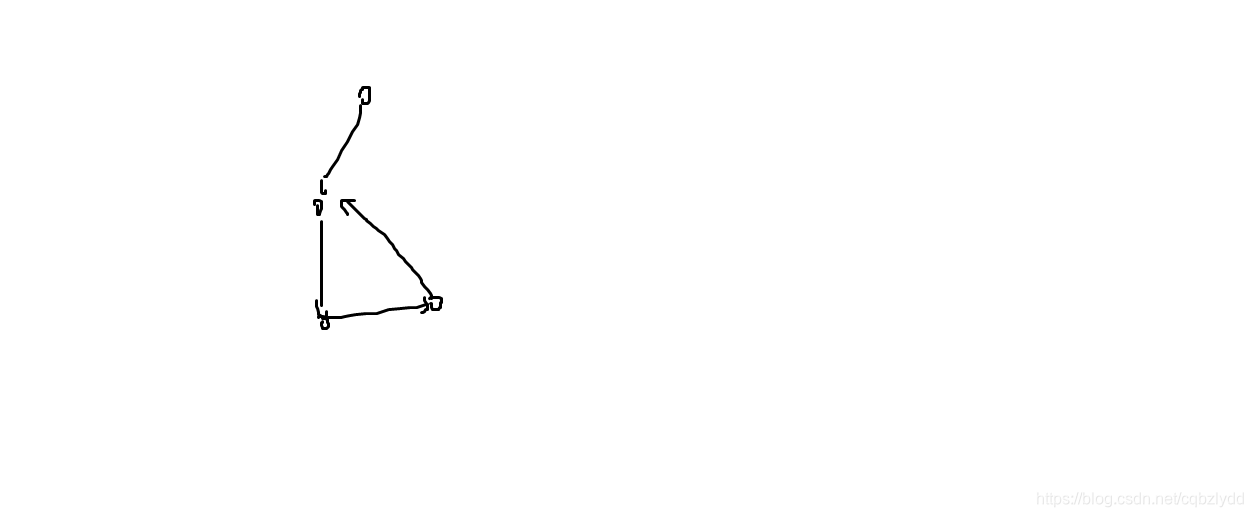
[POI2008]PLA-Postering
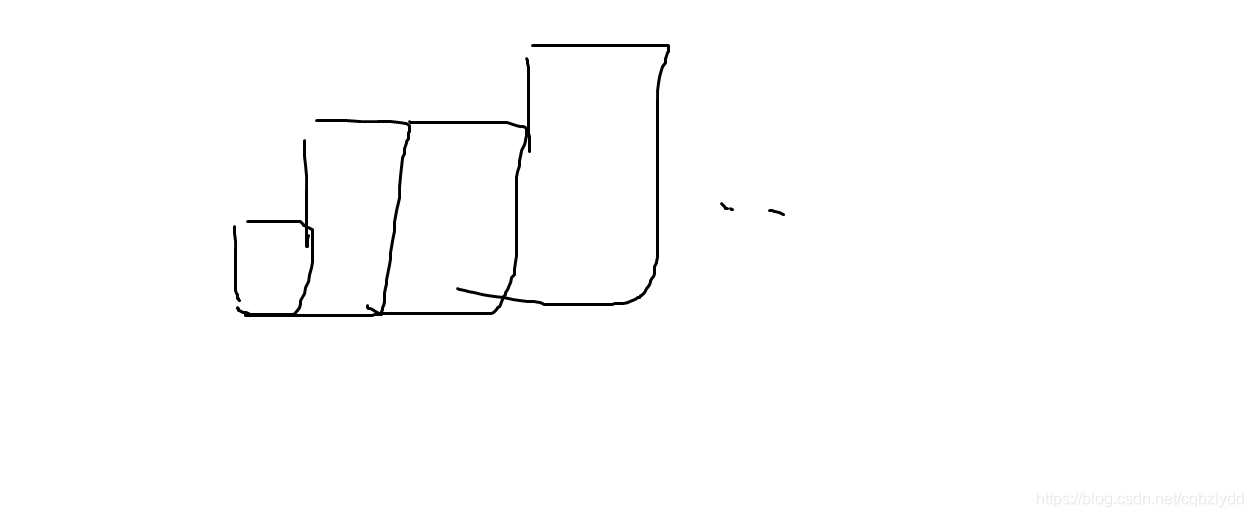
首先考虑高度单调递增的情况。可以一层一层的覆盖。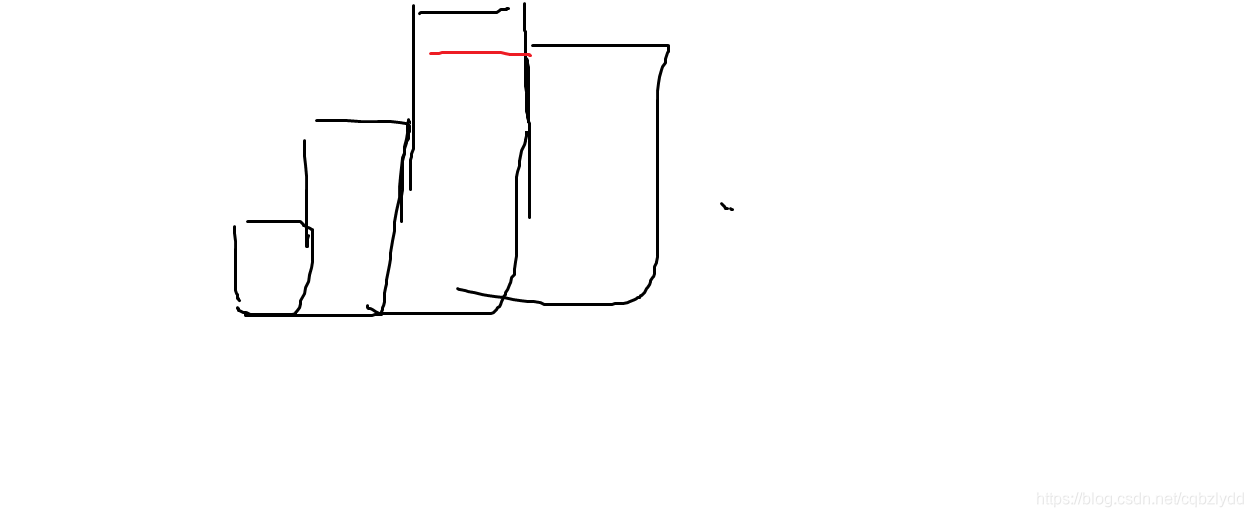
然后考虑有凸起部分的情况。可以发现必须花费一个代价横着涂,用单调栈维护,每次弹出元素时 ans++ ,最后把栈中元素个数加上即可。时间复杂度 O(n) 。
[POI2013]LAN-Colorful Chain
运用 莫队+桶 思想统计一下颜色出现次数即可。时间复杂度 O(n) 。
[POI2012]TOU-Tour de Byteotia
首先把两个节点编号 >k 的点加入进去,然后缩点。然后把剩下的边加进去,此时如果形成环就一定包含 <=k 的节点,可以用并查集统计答案。
[POI2013]BAJ-Bytecomputer
线性动态 dp 。分 -1/0/1 讨论转移即可。
代码:https://www.luogu.com.cn/record/48375712
[POI2013]TAK-Taxis
贪心结论题。
首先注意到,一定存在一个 X[i] 满足 X[i]>=A-B 。考虑枚举 i ,然后贪心的从大到小枚举即可。时间复杂度 O(n^2) 。
不难想到 X[i] 的函数图象是这样的:
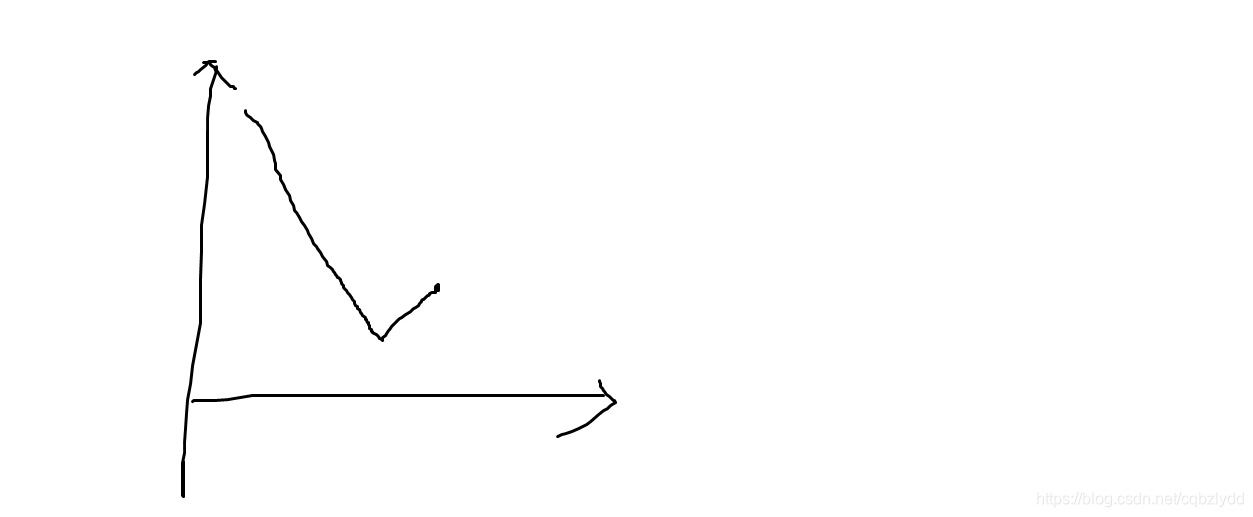
应取第一个 X[i]>=A-B。然后枚举即可,时间复杂度 O(n) 。
考虑反证法。假设存在 j 满足 X[j]>X[i] ,且 X[j] 作为最后一辆。此时假若交换 X[i] 和 X[j] 的位置,车子走的距离会更远,同时能够到达 A 点。证毕。
综上,我们有两种贪心方案:
- 从大到小选取
- 选取
X[i]作为最后一辆车,其余从大到小枚举。
时间复杂度 O(n) 。
代码:https://www.luogu.com.cn/record/53348652
[POI 2019] Pomniejszenie
贪心+大模拟。
首先想到从大到小枚举第一个不同的位数,这样可以保证数最大。
可以预处理 A[i] 表示前 i 个数不同的个数。第 i 位数比 b 小的条件是:l<=k&&k<=r ,其中 l=A[i-1]+(a[i]>=b[i]), r=A[i-1]+(a[i]!=0||b[i]!=1)+n-i 。对于 i 后面的数就很好讨论了。
代码:https://www.luogu.com.cn/record/53169249