[数据结构与算法]对称二叉树

这是蒟蒻认真写的第一篇题解，如有欠缺，请理解

题目描述

一棵有点权的有根树如果满足以下条件，则被轩轩称为对称二叉树：

1、二叉树；

2、将这棵树所有节点的左右子树交换，新树和原树对应位置的结构相同且点权相等。

下图中节点内的数字为权值，节点外的$id$表示节点编号。

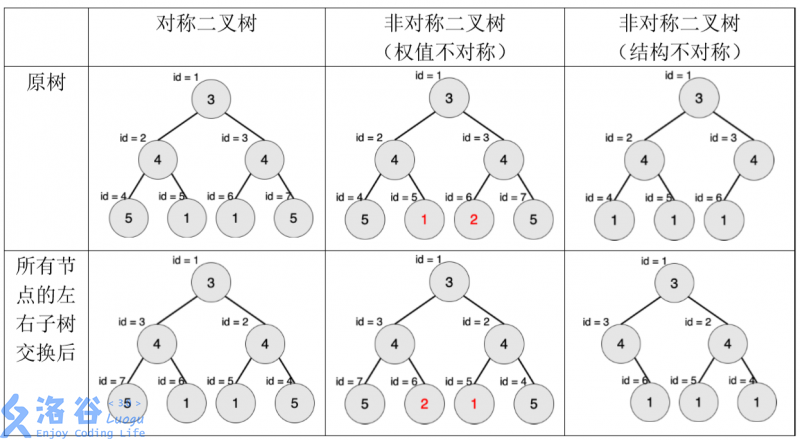
现在给出一棵二叉树，希望你找出它的一棵子树，该子树为对称二叉树，且节点数最多。请输出这棵子树的节点数。

注意：只有树根的树也是对称二叉树。本题中约定，以节点为$T$子树根的一棵“子树”指的是：节点$T$和它的全部后代节点构成的二叉树。

输入格式
第一行一个正整数$n$，表示给定的树的节点的数目，规定节点编号$1～n$，其中节点$1$输入格式
第一行一个正整数，表示给定的树的节点的数目，规定节点编号，其中节点是树根。

第二行$n$个正整数，用一个空格分隔，第$i$个正整数$v[i]$代表节点$i$的权值。

接下来$n$行，每行两个正整数$l[i],r[i]$，分别表示节点$i$的左右孩子的编号。如果不存在左 / 右孩子，则以$?1$表示。两个数之间用一个空格隔开。是树根。

第二行个正整数，用一个空格分隔，第个正整数代表节点的权值。

接下来行，每行两个正整数，分别表示节点的左右孩子的编号。如果不存在左 / 右孩子，则以表示。两个数之间用一个空格隔开。

样例

【输入样例 1】

2
1 3
2 -1
-1 -1

【输出样例 1】

1

【输入样例 2】

10
2 2 5 5 5 5 4 4 2 3
9 10
-1 -1
-1 -1
-1 -1
-1 -1
-1 2
3 4
5 6
-1 -1
7 8

【输出样例 2】

3

数据范围与提示

【输入输出样例 1 说明】

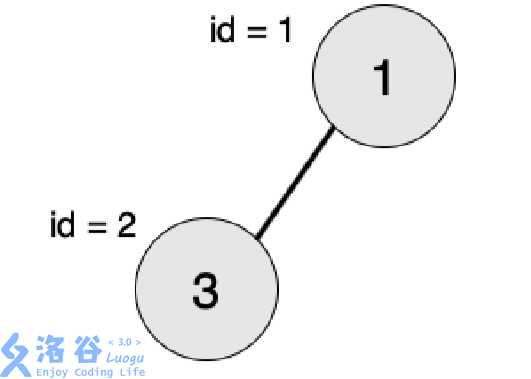
最大的对称二叉子树为以节点为$2$树根的子树，节点数为$1$。

【输入输出样例2说明】

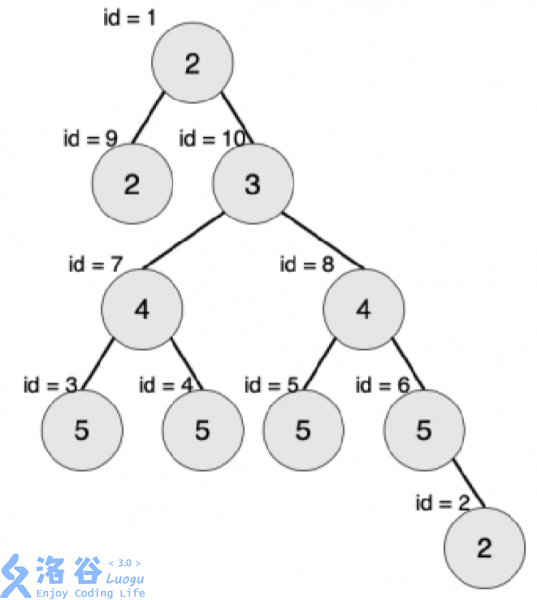
最大的对称二叉子树为以节点为$7$树根的子树，节点数为$3$。

【数据规模与约定】
共 $25$个测试点。
$v[i]\le 1000$
测试点 $1～3$, $n\le 10$，保证根结点的左子树的所有节点都没有右孩子，根结点的右 子树的所有节点都没有左孩子。
测试点 $4～8$, $n\le 10$。
测试点 $9～12$,$n\le 10^5$ ，保证输入是一棵“满二叉树” 。
测试点 $13～16$, $n\le 10^5$，保证输入是一棵“完全二叉树”。
测试点 $17～20$, $n\le 10^5$，保证输入的树的点权均为 11。
测试点 $21～25$, $n\le 10^6$。

本题约定：

层次：节点的层次从根开始定义起，根为第一层，根的孩子为第二层。树中任一节 点的层次等于其父亲节点的层次加 $1$。

树的深度：树中节点的最大层次称为树的深度。

满二叉树：设二叉树的深度为$h$，且二叉树有$2^h?1$个节点，这就是满二叉树。

思路

首先，要把对称二叉树的概念搞清楚，下图有很详细的解释

对称二叉树，权值要对称，然后结构也要对称。

简单分析一下题面:对称二叉树的最大结点数，最小是$1$，然后可以开始分析数据范围，不难发现输出1，3，6可以水很多分，当然3是最多的，如果是洛谷数据可以水到32分（好像是，不要问我怎么知道的），当然优秀的我们怎么可以水分，即便这是一道NOIP原题。

初始化存储在此不作赘余，相信刷到这题的树已经有些水准，关于孩子表示法，双亲表示法之类的，可以使代码条理化，其实也可开几个数组。

先用一个函数搜索以$i$为结点的最大对称二叉树，建议记忆化，省时间，又方便了后面的操作，注意如果搜索到节点为$?1$则代表已经无路可搜，即为出口，直接返回，接着继续遍历，以它的两个孩子为结点。

接下来是一个$check$函数，用以判断是否成立，现在就要用到$r[i]$了，如果当前结点的只有一个孩子都不相同，直接跳出，若是没有孩子，返回$true$，如果有两个孩子，继续判断它们的权值（即是$v[i]$），之后，想到对称二叉树的定义，第一个孩子的左孩子与第二个孩子的右孩子进行递归判断，第一个孩子的右孩子与第二个孩子的左孩子进行递归判断。

用一个变量存储答案，寻找结点满足要求的$dp[i]$最大值，最后输出，$over!$

最后总结一下，两个重要函数，缺一不可，第一个函数为第二个函数作铺垫，第二个函数为第一个函数返回值作判断，相辅相成。

代码时间

备注：此题题面制作不易，代码也考验思路，请先理解思路，不要直接TJ，珍惜一下作者的劳动成果，感谢您的理解

#include<bits/stdc++.h>
using namespace std;
int n,dp[1000005],ans;
struct Tree{
	int v,Lchild,Rchild;
}a[1000005];
int dfs(int x){
	if(x==-1)return 0;
	if(dp[x]!=0)return dp[x];
	return dp[x]=dfs(a[x].Lchild)+dfs(a[x].Rchild)+1;
}
bool check(int x,int y){
	int tot=0;
	if(x==-1)tot++;
	if(y==-1)tot++;
	if(tot==1)return false;
	if(tot==2)return true;
	if(a[x].v==a[y].v)return(check(a[x].Lchild,a[y].Rchild)&&check(a[y].Lchild,a[x].Rchild));
	else return false;
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++)scanf("%d",&a[i].v);
	for(int i=1;i<=n;i++)scanf("%d %d",&a[i].Lchild,&a[i].Rchild);
	dfs(1);
	for(int i=1;i<=n;i++){
		if(check(a[i].Lchild,a[i].Rchild)){
			ans=max(ans,dp[i]);
		}
	}
	printf("%d",ans);
	return 0;
}