连续队列 一般都是动态规划或者双指针 还有队列Queue
连个for循环一般可以使用双指针
先序
if (root == null) return;
print node.data
node.left,
node.right
斐波那契数列 0, 1, 1, 2, 3, 5, 8, https://blog.csdn.net/qq_42815754/article/details/84104359
public static long fibonacci(long number) { 输入n就会是第几个值
if ((number == 0) || (number == 1))
return number;
else
return fibonacci(number - 1) + fibonacci(number - 2); fn=fn-2 + fn-1 //递归调用
}
通过for循环的方式实现
long a =1l, b= 1l, c =0l; //定义三个long类型整数
for (int i = 0; i < n - 2; i++) {
c = a + b; //第3个数的值等于前两个数的和
a = b; //第2个数的值赋值给第1个数
b = c; //第3个数的值赋值给第2个数
}
动态规划 创建一个一维数组或者二维数组,保存每一个子问题的结果 通常用于求解具有某种最优性质的问题。在这类问题中,可能会有许多可行解
通过for循环和数组的方式实现
long[] arr = new long[n];
arr[0] = arr[1] = 1; //第一个和第二个数据特殊处理
for (int i = 2; i < n; i++) {
arr[i] = arr[i -2] + arr[i - 1];
//arr[n -1] = arr[i]; //数列第n个数 对应数组arr[n - 1] 因为数组下标是从0开始的
}
常见 https://blog.csdn.net/zw6161080123/article/details/80639932
组最大连续子序列和
int n = a.length;
int max = a[0];
int sum = a[0];
for(int i=1;i<n;i++){
sum = Math.max(sum+a[i], a[i]);
if(sum>=max){
max = sum;
}
}
台阶问题就是说,从0开始上台阶1,2,3…n,每次只能上1个或者2个台阶。问上到n个台阶有多少种走法
动态规划算法,f(n)=f(n-1)+f(n-2) 10阶台阶肯定是第九个台阶和是第八个台阶上来的,那第九个台阶肯定是第八个台阶和第七个台阶上来的
private int getSolution(int n){
if(n < 0){
return -1;
}
if(n == 0){
return 0;
}
if(n == 1){
return 1;
}
int a = 1;
int b = 1;
int fn = 0;
for(int i = 2; i < n+1; i++){
fn = a + b;
b = a;
a = fn;
}
return fn
}
如果台阶随意可以上,可以上1个,2个,3个…n个,那么n个台阶的话,有多种走法呢?
f(n)=f(n-1)+f(n-2)+…+f(4)+f(3)+f(2)+f(1)
f(n-1) = f(n-2) +f(n-3) +…+f(4)+f(3)+f(2)+f(1)
经过上面两个算式,我们可以得出,f(n)=2f(n-1)
private int getDoubleTree(int n){
if(n < 0){
return -1;
}
if(n0){
return 0;
}
if(n1){
return 0;
}
int a = 1;
int fn = 0;
for(int i = 2; i < n + 1; i++){
fn = 2*a;
a = fn;
}
return fn;
}
给定一个含有 n 个正整数的数组和一个正整数 target 。找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
public int minSubArrayLen(int s, int[] nums) {
int n = nums.length;
if (n == 0) {
return 0;
}
int ans = Integer.MAX_VALUE;
int start = 0, end = 0;
int sum = 0;
while (end < n) {
sum += nums[end];
while (sum >= s) {
ans = Math.min(ans, end - start + 1);
sum -= nums[start];
start++;
}
end++;
}
return ans == Integer.MAX_VALUE ? 0 : ans;
}
时间复杂度:O(n)O(n),其中 nn 是数组的长度。指针 \textit{start}start 和 \textit{end}end 最多各移动 nn 次。
空间复杂度:O(1)
时间复杂段 就是需要运行的次数T,挪动的次数
空间复杂度 是否新分配内存O 数组,map都算新建内存了 没建就为o1
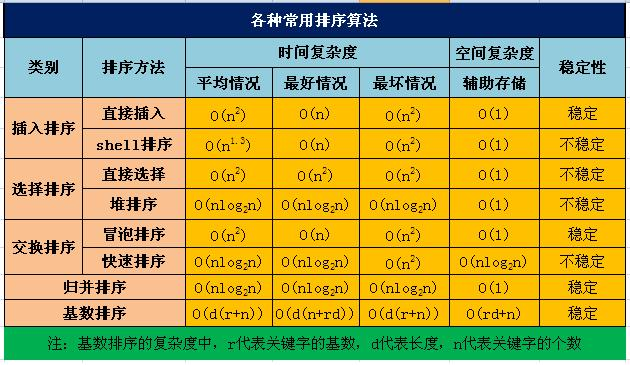
!!!泡排序在找最大元素时,边比较边交换
!!!选择排序 先找到数组中最小的元素,与数组第一个元素交换位置,然后找出剩余元素中最小的元素,与数组第二个位置交换
插入排序 要移动位置
归并排序 递归 二分法
int mid = left + (right - left) / 2;
//治
sort(arr, left, mid);
sort(arr, mid + 1, right);
从数组中选择一个元素作为中轴元素(一般选第一个元素,或者也可随机获取),将小于中轴元素的元素放在中轴元素左边,大于中轴元素的放在中轴元素右边,此时中轴元素有序。然后,将中轴元素左边部分和右边部分也重复同样的操作(通过递归),直到数组的大小为1,此时每个元素都有序。
快速排序最差时间复杂度 n2次
1)数组已经是正序(same order)排过序的。
2)数组已经是倒序排过序的。
3)所有的元素都相同(1、2的特殊情况
堆排序是不稳定的 将堆顶元素与最后一个元素交换,将剩余元素再次构成一个二叉堆,再把堆顶元素与第二个元素交换…
最大/小的元素,topK之类,这时候堆排序的优势就出来了。
每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆
几大算法https://blog.csdn.net/qq_43341422/article/details/108857393