文章目录
1. 理论基础
1.1 决策树
分类决策树模型是表示基于特征对实例进行分类的树形结构。决策树可以转换成一个if-then规则的集合,也可以看作是定义在特征空间划分上的类的条件概率分布。
决策树学习旨在构建一个与训练数据拟合很好,并且复杂度小的决策树。因为从可能的决策树中直接选取最优决策树是NP完全问题。现实中采用启发式方法学习次优的决策树。
决策树学习算法包括3部分:特征选择、树的生成和树的剪枝。常用的算法有ID3、C4.5和CART。
1.2 特征选择
特征选择的目的在于选取对训练数据能够分类的特征。特征选择的关键是其准则。常用的准则如下:
信息增益
样本集合 D D D对特征 A A A的信息增益(ID3)
g ( D , A ) = H ( D ) ? H ( D ∣ A ) g(D, A)=H(D)-H(D|A) g(D,A)=H(D)?H(D∣A)
H ( D ) = ? ∑ k = 1 K ∣ C k ∣ ∣ D ∣ log ? 2 ∣ C k ∣ ∣ D ∣ H(D)=-\sum_{k=1}^{K} \frac{\left|C_{k}\right|}{|D|} \log _{2} \frac{\left|C_{k}\right|}{|D|} H(D)=?k=1∑K?∣D∣∣Ck?∣?log2?∣D∣∣Ck?∣?
H ( D ∣ A ) = ∑ i = 1 n ∣ D i ∣ ∣ D ∣ H ( D i ) H(D | A)=\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} H\left(D_{i}\right) H(D∣A)=i=1∑n?∣D∣∣Di?∣?H(Di?)
其中, H ( D ) H(D) H(D)是数据集 D D D的熵, H ( D i ) H(D_i) H(Di?)是数据集 D i D_i Di?的熵, H ( D ∣ A ) H(D|A) H(D∣A)是数据集 D D D对特征 A A A的条件熵。 D i D_i Di?是 D D D中特征 A A A取第 i i i个值的样本子集, C k C_k Ck?是 D D D中属于第 k k k类的样本子集。 n n n是特征 A A A取 值的个数, K K K是类的个数。
信息增益比
样本集合 D D D对特征 A A A的信息增益比(C4.5)
g R ( D , A ) = g ( D , A ) H ( D ) g_R(D, A)=\frac{g(D, A)}{H(D)} gR?(D,A)=H(D)g(D,A)?
其中, g ( D , A ) g(D,A) g(D,A)是信息增益, H ( D ) H(D) H(D)是数据集 D D D关于特征 A 的熵。
使用信息增益比的目的:特征选择往往会选择特征取值较多的特征,如 ID
基尼指数
样本集合 D D D的基尼指数(CART)
Gini ? ( D ) = 1 ? ∑ k = 1 K ( ∣ C k ∣ ∣ D ∣ ) 2 \operatorname{Gini}(D)=1-\sum_{k=1}^{K}\left(\frac{\left|C_{k}\right|}{|D|}\right)^{2} Gini(D)=1?k=1∑K?(∣D∣∣Ck?∣?)2
特征 A A A条件下集合 D D D的基尼指数:
Gini ? ( D , A ) = ∣ D 1 ∣ ∣ D ∣ Gini ? ( D 1 ) + ∣ D 2 ∣ ∣ D ∣ Gini ? ( D 2 ) \operatorname{Gini}(D, A)=\frac{\left|D_{1}\right|}{|D|} \operatorname{Gini}\left(D_{1}\right)+\frac{\left|D_{2}\right|}{|D|} \operatorname{Gini}\left(D_{2}\right) Gini(D,A)=∣D∣∣D1?∣?Gini(D1?)+∣D∣∣D2?∣?Gini(D2?)
1.3 决策树的生成
通常使用 信息增益最大、信息增益比最大或基尼指数最小 作为特征选择的准则。决策树的生成往往通过计算信息增益或其他指标,从根结点开始,递归地产生决策树。这相当于用信息增益或其他准则不断地选取局部最优的特征,或将训练集分割为能够基本正确分类的子集。
1.4 剪枝
由于生成的决策树存在过拟合问题,需要对它进行剪枝,以简化学到的决策树。决策树的剪枝,往往从已生成的树上剪掉一些叶结点或叶结点以上的子树,并将其父结点或根结点作为新的叶结点,从而简化生成的决策树。
2. 利用 C4.5 算法构建决策树
2.1 数据集
给定下面的数据集,通过年龄、有无工作、有无房子和信贷情况来判决是否可以贷款:
def create_data():
datasets = [['青年', '否', '否', '一般', '否'],
['青年', '否', '否', '好', '否'],
['青年', '是', '否', '好', '是'],
['青年', '是', '是', '一般', '是'],
['青年', '否', '否', '一般', '否'],
['中年', '否', '否', '一般', '否'],
['中年', '否', '否', '好', '否'],
['中年', '是', '是', '好', '是'],
['中年', '否', '是', '非常好', '是'],
['中年', '否', '是', '非常好', '是'],
['老年', '否', '是', '非常好', '是'],
['老年', '否', '是', '好', '是'],
['老年', '是', '否', '好', '是'],
['老年', '是', '否', '非常好', '是'],
['老年', '否', '否', '一般', '否'],
]
labels = [u'年龄', u'有工作', u'有自己的房子', u'信贷情况', u'类别']
# 返回数据集和每个维度的名称
return datasets, labels
2.2 计算熵
C4.5 算法基于信息增益比,因此需要计算熵和条件上,从而计算信息增益,最后计算信息增益比:
# 计算信息熵
def calculate_entropy(datasets):
datasets = np.array(datasets)
sample_number = len(datasets)
freq = Counter(datasets[:, -1]).most_common()
probabilities = [item[1] / sample_number for item in freq]
ent = - sum([p * math.log(p, 2) for p in probabilities])
return ent
# 条件熵
def calculate_cond_entropy(datasets, axis):
feature_sets = {}
for data in datasets:
feature = data[axis]
if feature not in feature_sets:
feature_sets[feature] = []
feature_sets[feature].append(data)
cond_ent = sum([len(d) / len(datasets) * calculate_entropy(d) for d in feature_sets.values()])
return cond_ent
# 信息增益
def info_gain(ent, cond_ent):
return ent - cond_ent
def info_gains(datasets):
axises = [i for i in range(len(datasets[0])-1)]
ent = calculate_entropy(datasets)
best_feature = []
for axis in axises:
info_gain_axis = info_gain(ent, calculate_cond_entropy(datasets, axis))
best_feature.append((axis, info_gain_axis))
print(f'feature: {labels[axis]}\tinfo_gain: {info_gain_axis}')
best_feature = max(best_feature, key=lambda x: x[-1])
return best_feature
best_feature = info_gains(datasets)
print(labels[best_feature[0]])
结果如下:
feature: 年龄 info_gain: 0.08300749985576883
feature: 有工作 info_gain: 0.32365019815155627
feature: 有自己的房子 info_gain: 0.4199730940219749
feature: 信贷情况 info_gain: 0.36298956253708536
有自己的房子
2.3 构建模型
2.3.1 节点 Node
root 为 True 代表当前节点为最底层叶节点,tree 存储了子树,在构建 DT(Decision Tree) 时通过递归将树 tree 加深:
# 定义节点类 二叉树
class Node:
def __init__(self, root=True, label=None, feature_name=None, feature=None):
self.root = root
self.label = label
self.feature_name = feature_name
self.feature = feature
self.tree = {}
self.result = {
'label:': self.label,
'feature': self.feature,
'tree': self.tree
}
def __repr__(self):
return '{}'.format(self.result)
def add_node(self, val, node):
self.tree[val] = node
def predict(self, features):
if self.root is True:
return self.label
return self.tree[features[self.feature]].predict(features)
2.3.2 Decision Tree
首先,将计算熵的函数添加到类 DTree 中,接着通过 递归 的方式构建 DTree:
class DTree:
def __init__(self, epsilon=0.1):
self.epsilon = epsilon
self._tree = {}
# 熵
@staticmethod
def calc_ent(datasets):
data_length = len(datasets)
label_count = {}
for i in range(data_length):
label = datasets[i][-1]
if label not in label_count:
label_count[label] = 0
label_count[label] += 1
ent = -sum([(p / data_length) * log(p / data_length, 2)
for p in label_count.values()])
return ent
# 经验条件熵
def cond_ent(self, datasets, axis=0):
data_length = len(datasets)
feature_sets = {}
for i in range(data_length):
feature = datasets[i][axis]
if feature not in feature_sets:
feature_sets[feature] = []
feature_sets[feature].append(datasets[i])
cond_ent = sum([(len(p) / data_length) * self.calc_ent(p)
for p in feature_sets.values()])
return cond_ent
# 信息增益
@staticmethod
def info_gain(ent, cond_ent):
return ent - cond_ent
def info_gain_train(self, datasets):
count = len(datasets[0]) - 1
ent = self.calc_ent(datasets)
best_feature = []
for c in range(count):
c_info_gain = self.info_gain(ent, self.cond_ent(datasets, axis=c))
best_feature.append((c, c_info_gain))
# 比较大小
best_ = max(best_feature, key=lambda x: x[-1])
return best_
def train(self, train_data):
"""
input:数据集D(DataFrame格式),特征集A,阈值eta
output:决策树T
"""
_, y_train, features = train_data.iloc[:, :
-1], train_data.iloc[:,
-1], train_data.columns[:
-1]
# 1,若D中实例属于同一类Ck,则T为单节点树,并将类Ck作为结点的类标记,返回T
if len(y_train.value_counts()) == 1:
return Node(root=True, label=y_train.iloc[0])
# 2, 若A为空,则T为单节点树,将D中实例树最大的类Ck作为该节点的类标记,返回T
if len(features) == 0:
return Node(
root=True,
label=y_train.value_counts().sort_values(
ascending=False).index[0])
# 3,计算最大信息增益 同5.1,Ag为信息增益最大的特征
max_feature, max_info_gain = self.info_gain_train(np.array(train_data))
max_feature_name = features[max_feature]
# 4,Ag的信息增益小于阈值eta,则置T为单节点树,并将D中是实例数最大的类Ck作为该节点的类标记,返回T
if max_info_gain < self.epsilon:
return Node(
root=True,
label=y_train.value_counts().sort_values(
ascending=False).index[0])
# 5,构建Ag子集
node_tree = Node(
root=False, feature_name=max_feature_name, feature=max_feature)
feature_list = train_data[max_feature_name].value_counts().index
for f in feature_list:
sub_train_df = train_data.loc[train_data[max_feature_name] ==
f].drop([max_feature_name], axis=1)
# 6, 递归生成树
sub_tree = self.train(sub_train_df)
node_tree.add_node(f, sub_tree)
# pprint.pprint(node_tree.tree)
return node_tree
def fit(self, train_data):
self._tree = self.train(train_data)
return self._tree
def predict(self, X_test):
return self._tree.predict(X_test)
2.4 测试
datasets, labels = create_data()
data_df = pd.DataFrame(datasets, columns=labels)
dt = DTree()
tree = dt.fit(data_df)
print(tree)
print(dt.predict(['老年', '否', '否', '一般'])) # 否
结果如下(得到一颗由字典表示的树):
{'label:': None, 'feature': 2, 'tree': {'否': {'label:': None, 'feature': 1, 'tree': {'否': {'label:': '否', 'feature': None, 'tree': {}}, '是': {'label:': '是', 'feature': None, 'tree': {}}}}, '是': {'label:': '是', 'feature': None, 'tree': {}}}}
3. sklearn 实例
在 sklearn.tree 模块中有 DecisionTreeClassifier 模型:

Python 程序如下:
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
def create_data():
iris = load_iris()
df = pd.DataFrame(
data=iris.data,
columns=iris.feature_names)
df['label'] = iris.target
df.columns = [
'sepal length', 'sepal width',
'petal length' ,'petal width', 'label']
data = np.array(df.iloc[:100, [0, 1, -1]])
return data[:, [0, 1]], data[:, -1], df
X, y, df = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
clf = DecisionTreeClassifier(criterion='gini')
clf.fit(X_train, y_train)
score = clf.score(X_test, y_test)
print(score)
DecisionTreeClassifier 的默认选择特征根据 gini 最小,输出结果如下:
0.933333
成功率 93.3% 🍻
此外,我们可以使用 sklearn.tree.plot_tree 绘制出决策树:
from sklearn import tree
import matplotlib.pyplot as plt
feature_names = load_iris().feature_names
plt.figure(figsize=(10, 8))
tree.plot_tree(clf, filled = True, feature_names=df.columns)
plt.savefig('./tree.png')
plt.show()
结果如下:
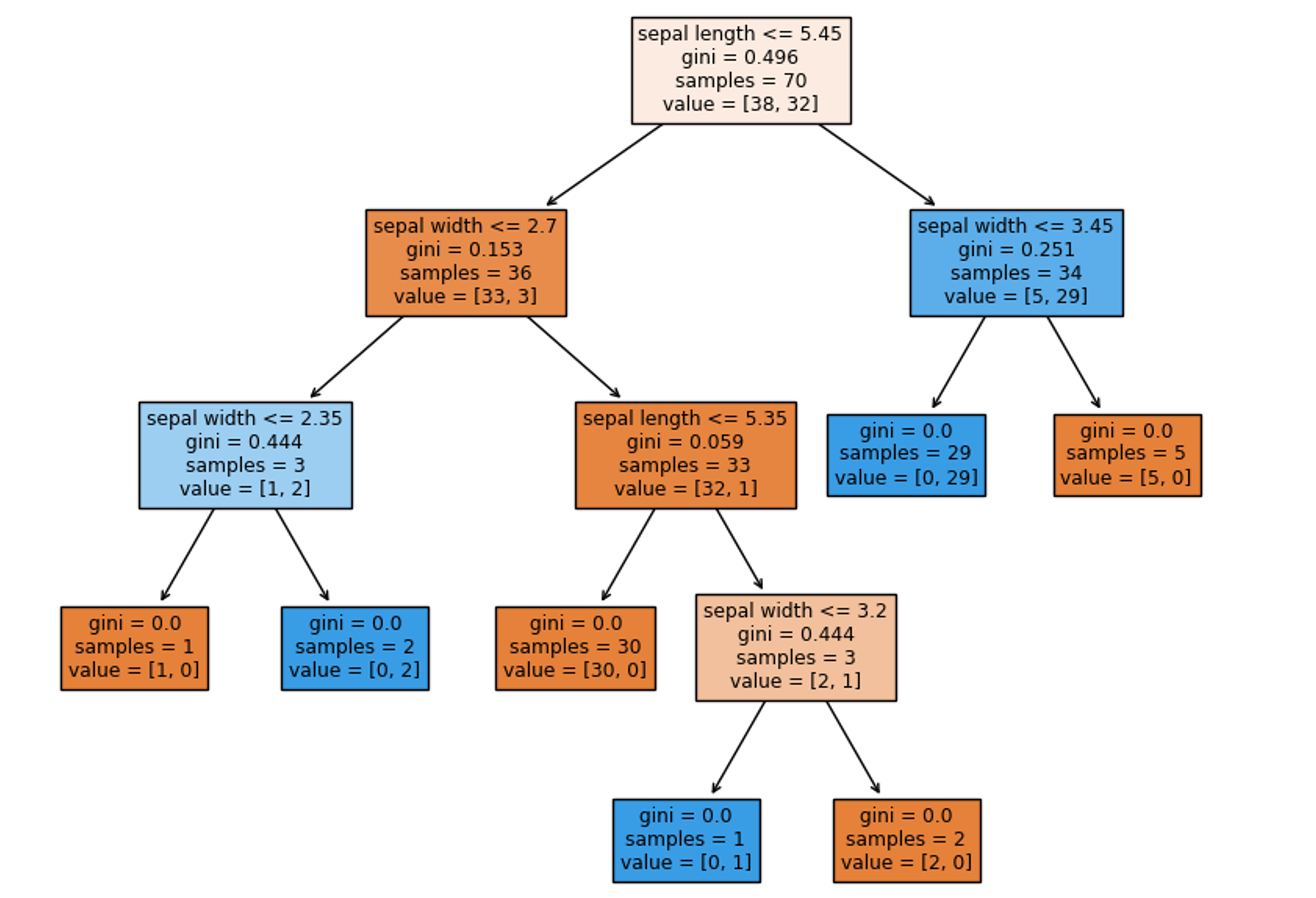
以上就是所有内容了,决策树数学理论理解起来很简单;
但自己构建决策树遇到了好多坑,尤其是选择数据结构和操作矩阵,继续努力呀 🍻
REFERENCE:
- 李航统计学习方法
- sklearn.tree.DecisionTreeClassifier
- Introduction to Machine Learning with Python